Статья опубликована в рамках: XII Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ЭКОНОМИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 08 октября 2013 г.)
Наука: Экономика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
отправлен участнику
ЗАДАЧА ОПТИМАЛЬНОГО ИМПУЛЬСНОГО УПРАВЛЕНИЯ В МОДЕЛИ ФИРМЫ С ОБУЧЕНИЕМ РАБОТНИКОВ НОВОЙ ИНФОРМАЦИОННОЙ ТЕХНОЛОГИИ
Адушинова Наталья Александровна
студент 5 курса, кафедра методов оптимизации ФГБОУ ВПО «ИГУ», Институт математики, экономики и информатики, г. Иркутск
E-mail: actualis@bk.ru
Самсонюк Ольга Николаевна,
научный руководитель. канд. ф.-м. наук, доцент, ФГБОУ ВПО «ИГУ», Институт математики, экономики и информатики, г. Иркутск
Работа выполнена при частичной финансовой поддержке ФЦП «Научные и научно-педагогические кадры инновационной России», соглашение 8211 от 06.08.2012.
1. Введение
В статье рассматривается частный вариант модели фирмы, выпуск продукции которой зависит от уровня освоения её работниками новой производственной технологии. Предполагается, что обучение работников происходит как вследствие их контакта с уже обученными, так и при целенаправленных действиях со стороны руководства фирмы, допускающих обучение с высокой интенсивностью в течение кратких промежутков времени (например, краткосрочные курсы повышения квалификации). Последнее приводит к быстрому, почти скачкообразному, увеличению количества работников, владеющих инновациями. В статье исследуется упрощенный вариант модели, в котором объемы основного капитала и трудовых ресурсов не меняются на рассматриваемом промежутке времени, и, как следствие, доход фирмы зависит только от степени освоения инновационной производственной технологии. Однако предположения, допускающие скачкообразные изменения количества обученных работников, приводят к появлению в этой модели задачи оптимального управления с разрывными траекториями (задачи оптимального импульсного управления) и использованию неклассических методов исследования [1].
2. Описание модели
Пусть фирма производит некоторый товар, выпуск которого по традиционной технологии описывается производственной функцией ![]() где
где ![]() — объем основного капитала,
— объем основного капитала, ![]() — объем трудовых ресурсов. Известно, что использование производственных инноваций может дать прирост выпуска на величину
— объем трудовых ресурсов. Известно, что использование производственных инноваций может дать прирост выпуска на величину ![]() в случае, когда все работники фирмы знакомы с нововведениями и могут их применять. Обозначим через
в случае, когда все работники фирмы знакомы с нововведениями и могут их применять. Обозначим через ![]() — объем трудовых ресурсов, способных использовать новую технологию. Тогда производственная функция фирмы имеет вид
— объем трудовых ресурсов, способных использовать новую технологию. Тогда производственная функция фирмы имеет вид ![]() Таким образом, выпуск фирмы складывается из выпуска по традиционному способу и дополнительного выпуска, полученного вследствие применения частью работников улучшенного способа производства. Предположим, что на рассматриваемом промежутке времени величины
Таким образом, выпуск фирмы складывается из выпуска по традиционному способу и дополнительного выпуска, полученного вследствие применения частью работников улучшенного способа производства. Предположим, что на рассматриваемом промежутке времени величины ![]() и
и ![]() не изменяются, и доход фирмы описывается функцией
не изменяются, и доход фирмы описывается функцией ![]() где
где ![]() — цена единицы продукции,
— цена единицы продукции, ![]()
![]() Уровень освоения работниками фирмы новой технологии
Уровень освоения работниками фирмы новой технологии ![]() может возрастать при общении работников между собой, а также в результате их обучения со стороны руководства фирмы. Кроме того, часть работников, владеющих новой технологией, утрачивает навыки в результате забывания. Предполагается, что темп забывания постоянен и равен
может возрастать при общении работников между собой, а также в результате их обучения со стороны руководства фирмы. Кроме того, часть работников, владеющих новой технологией, утрачивает навыки в результате забывания. Предполагается, что темп забывания постоянен и равен ![]() Уравнение динамики
Уравнение динамики ![]() имеет следующий вид
имеет следующий вид
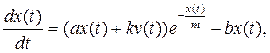
![]() (1)
(1)
![]()
![]() (2)
(2)
где ![]() задает текущие усилия руководства фирмы, направленные на обучение сотрудников, а
задает текущие усилия руководства фирмы, направленные на обучение сотрудников, а ![]() — объем трудовых ресурсов, знакомых с новой технологией в начальный момент времени. Прокомментируем динамическую систему (1), (2). В уравнении (1) первое слагаемое означает, что прирост числа обученных работников в момент времени
— объем трудовых ресурсов, знакомых с новой технологией в начальный момент времени. Прокомментируем динамическую систему (1), (2). В уравнении (1) первое слагаемое означает, что прирост числа обученных работников в момент времени ![]() пропорционален текущему уровню
пропорционален текущему уровню ![]() в совокупности с усилиями руководства и, кроме того, пропорционален множителю
в совокупности с усилиями руководства и, кроме того, пропорционален множителю ![]() Смысл множителя
Смысл множителя ![]() состоит в том, что обучение в первую очередь охватывает наиболее заинтересованных, расположенных к нему работников, и, следовательно, чем больше человек уже освоило данную технологию, тем сложнее обучить остальных. Второе слагаемое в (1) характеризует снижение уровня
состоит в том, что обучение в первую очередь охватывает наиболее заинтересованных, расположенных к нему работников, и, следовательно, чем больше человек уже освоило данную технологию, тем сложнее обучить остальных. Второе слагаемое в (1) характеризует снижение уровня ![]() в результате забывания или утраты навыков.
в результате забывания или утраты навыков.
Все параметры в (1), (2) неотрицательны и имеют следующий смысл: ![]() характеризует эффективность внутреннего взаимодействия сотрудников,
характеризует эффективность внутреннего взаимодействия сотрудников, ![]() — эффективность обучения при применении единицы усилий со стороны руководства,
— эффективность обучения при применении единицы усилий со стороны руководства, ![]() — темп забывания,
— темп забывания, ![]() — уровень освоивших новую технологию, при котором происходит наиболее эффективное обучение работников.
— уровень освоивших новую технологию, при котором происходит наиболее эффективное обучение работников.
Рассмотрим уравнение (1) при отсутствии внешнего обучения, т. е. при ![]() Запишем (1) в следующем виде
Запишем (1) в следующем виде
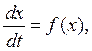
![]()
Здесь ![]() задает функцию роста трудовых ресурсов, владеющих новой технологией. График
задает функцию роста трудовых ресурсов, владеющих новой технологией. График ![]() при значениях параметров
при значениях параметров ![]()
![]()
![]() приведен на Рис.1, где
приведен на Рис.1, где ![]() ,
, ![]() ,
, ![]() . Охарактеризуем функцию
. Охарактеризуем функцию ![]() на промежутках
на промежутках ![]()
![]()
![]() и
и ![]()

Рисунок 1. График функции f(x) при a = 10, m = 30, b = 0,1
· При начальном небольшом количестве работников, владеющих новой технологией, т. е. ![]() скорость освоения новой технологии возрастает, что объясняется интересом к ней наиболее активных и любознательных работников. Таким образом,
скорость освоения новой технологии возрастает, что объясняется интересом к ней наиболее активных и любознательных работников. Таким образом, ![]() отражает уровень, соответствующий максимальной скорости обучаемости работников. Функция
отражает уровень, соответствующий максимальной скорости обучаемости работников. Функция ![]() на промежутке
на промежутке ![]() возрастает и является вогнутой.
возрастает и является вогнутой.
· При ![]() скорость обучения путем взаимодействия работников друг с другом (внутреннее обучение) снижается, поскольку теперь в этот процесс вовлекаются менее заинтересованные слои трудового коллектива. При этом с каждым дополнительным работником, освоившим технологию, происходит большее замедление скорости внутреннего обучения. Здесь, функция
скорость обучения путем взаимодействия работников друг с другом (внутреннее обучение) снижается, поскольку теперь в этот процесс вовлекаются менее заинтересованные слои трудового коллектива. При этом с каждым дополнительным работником, освоившим технологию, происходит большее замедление скорости внутреннего обучения. Здесь, функция ![]() убывает и является вогнутой.
убывает и является вогнутой.
· При ![]() в обучение вовлекаются еще более инертные слои. Функция
в обучение вовлекаются еще более инертные слои. Функция ![]() убывает и является выпуклой. Скорость обучения не высока, и каждому дополнительному обученному работнику соответствует меньшее ее снижение.
убывает и является выпуклой. Скорость обучения не высока, и каждому дополнительному обученному работнику соответствует меньшее ее снижение.
· При ![]() скорость внутреннего обучения отрицательна. Величина
скорость внутреннего обучения отрицательна. Величина ![]() характеризует объем трудовых ресурсов, не проявляющих самостоятельного интереса к инновациям или не способных к самообучению.
характеризует объем трудовых ресурсов, не проявляющих самостоятельного интереса к инновациям или не способных к самообучению.
На Рис. 2 и 3 приведены результаты качественного исследования уравнения (1) при ![]() и набросок семейства интегральных кривых. Для любого начального условия
и набросок семейства интегральных кривых. Для любого начального условия ![]() интегральные кривые при
интегральные кривые при ![]() стремятся к уровню насыщения
стремятся к уровню насыщения ![]()
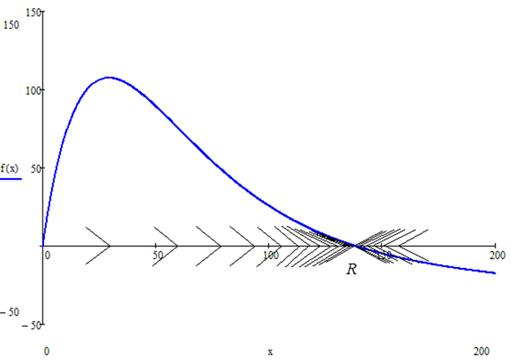
Рисунок 2. Фазовый портрет
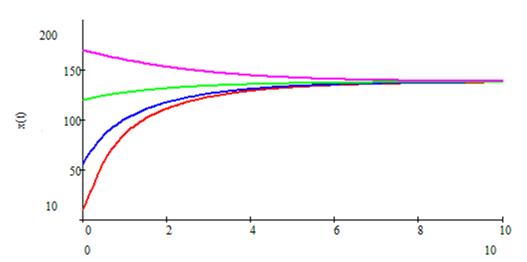
Рисунок 3. Семейство интегральных кривых
Введение внешнего обучения в уравнение (1) позволяет увеличить уровень насыщения и, тем самым, добиться того, чтобы новой технологией овладело большее число работников, что приведет к увеличению выпуска продукции и дохода. Суммарный доход фирмы описывается интегралом 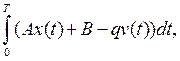 где
где ![]() — текущие затраты фирмы, направленные на обучение работников,
— текущие затраты фирмы, направленные на обучение работников, ![]() — горизонт планирования.
— горизонт планирования.
Рассмотрим задачу выбора такой стратегии обучения ![]() , при которой суммарный доход фирмы будет наибольшим, т. е.
, при которой суммарный доход фирмы будет наибольшим, т. е.
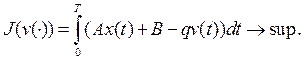 (3)
(3)
Задача (1)—(3) является задачей оптимального управления, в которой ![]() — траектория, а
— траектория, а ![]() — управление. Особенность этой задачи состоит в том, что управление
— управление. Особенность этой задачи состоит в том, что управление ![]() входит в правую часть уравнения динамики (1) линейно и не является ограниченным сверху. Это означает, что хотя суммарные расходы, затрачиваемые руководством фирмы на обучение персонала, ограничены, но их интенсивность может быть сколь угодно большой в течение краткого промежутка времени, т. е. допускается в некотором смысле «агрессивное» обучение, приводящее к почти скачкообразным изменениям уровня освоения новой технологией. Указанная особенность приводит к тому, что в классе кусочно-непрерывных управлений данная задача не имеет решения.
входит в правую часть уравнения динамики (1) линейно и не является ограниченным сверху. Это означает, что хотя суммарные расходы, затрачиваемые руководством фирмы на обучение персонала, ограничены, но их интенсивность может быть сколь угодно большой в течение краткого промежутка времени, т. е. допускается в некотором смысле «агрессивное» обучение, приводящее к почти скачкообразным изменениям уровня освоения новой технологией. Указанная особенность приводит к тому, что в классе кусочно-непрерывных управлений данная задача не имеет решения.
Будем рассматривать задачу (1)—(3) в расширенной постановке, учитывающей возможность «агрессивного» обучения и скачки уровня ![]() Соответствующая задача оптимального управления с разрывными траекториями описывается следующими соотношениями [1]:
Соответствующая задача оптимального управления с разрывными траекториями описывается следующими соотношениями [1]:
![]() (4)
(4)
![]()
![]()
![]() (5)
(5)
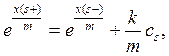
![]()
![]() (6)
(6)
![]()
![]() (7)
(7)
![]()
![]()
![]()
![]() (8)
(8)
Управлением в задаче (4)-(8) является набор ![]() , в котором кусочно-непрерывная функция
, в котором кусочно-непрерывная функция ![]() описывает усилия руководства фирмы, направленные на обычное обучение,
описывает усилия руководства фирмы, направленные на обычное обучение, ![]() — множество моментов времени
— множество моментов времени ![]() , в которых проводится обучение с высокой интенсивностью,
, в которых проводится обучение с высокой интенсивностью, ![]() — интенсивность обучения в момент
— интенсивность обучения в момент ![]() Ограничение на управление задается соотношениями (8). Предполагается, что
Ограничение на управление задается соотношениями (8). Предполагается, что  где
где ![]() задает ограничение по суммарным расходам на обучение работников. Кусочно-непрерывные функции
задает ограничение по суммарным расходам на обучение работников. Кусочно-непрерывные функции ![]() и
и ![]() — траектории. На промежутках, не включающих точки множества
— траектории. На промежутках, не включающих точки множества ![]() , они удовлетворяют системе дифференциальных уравнений (5), а в точках множества
, они удовлетворяют системе дифференциальных уравнений (5), а в точках множества ![]() — условию скачка (6). Заметим, что функция
— условию скачка (6). Заметим, что функция ![]() появляется при переходе от интегрального функционала к терминальному, а именно, в задаче (1)—(3)
появляется при переходе от интегрального функционала к терминальному, а именно, в задаче (1)—(3) ![]() где
где
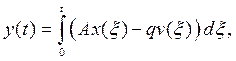 (9)
(9)
и после расширения задачи (1)-(3) до задачи с разрывными траекториями и отбрасывания слагаемого ![]() получаем критерий качества (4). Цель управления в задаче (4)—(8) состоит в нахождении такой стратегии обучения работников
получаем критерий качества (4). Цель управления в задаче (4)—(8) состоит в нахождении такой стратегии обучения работников ![]() , при которой функционал качества (4) принимает наибольшее значение.
, при которой функционал качества (4) принимает наибольшее значение.
Назовем допустимым процессом задачи (4)-(8) набор ![]() , состоящий из кусочно-непрерывных траекторий
, состоящий из кусочно-непрерывных траекторий ![]() и управления
и управления ![]() , удовлетворяющих соотношениям (5)-(8). Назовем
, удовлетворяющих соотношениям (5)-(8). Назовем ![]() оптимальным процессом задачи (4)-(8), если для всех допустимых процессов
оптимальным процессом задачи (4)-(8), если для всех допустимых процессов ![]() выполняется неравенство
выполняется неравенство ![]()
Сделаем два замечания [1].
Замечание 1. Допустимое управление ![]() по сути является неотрицательной мерой Лебега-Стилтьеса и может быть записано в следующем виде
по сути является неотрицательной мерой Лебега-Стилтьеса и может быть записано в следующем виде
![]()
где: ![]() — дельта-функция Дирака, сосредоточенная в точке
— дельта-функция Дирака, сосредоточенная в точке ![]() Такие управления принято называть импульсными, а задачу вида (4)—(8) — задачей оптимального импульсного управления.
Такие управления принято называть импульсными, а задачу вида (4)—(8) — задачей оптимального импульсного управления.
Замечание 2. Для любого допустимого процесса ![]() найдется последовательность
найдется последовательность ![]() состоящая из троек функций
состоящая из троек функций ![]() удовлетворяющих (1), (2) и (9), такая, что функции
удовлетворяющих (1), (2) и (9), такая, что функции ![]() сходятся к
сходятся к ![]() в точках непрерывности, а
в точках непрерывности, а ![]() в смысле сходимости мер. Таким образом, любая траектория задачи (4)—-(8) может быть приближена последовательностью траекторий задачи (1)—(3).
в смысле сходимости мер. Таким образом, любая траектория задачи (4)—-(8) может быть приближена последовательностью траекторий задачи (1)—(3).
Исследуем задачу (4)—(8) при помощи необходимых условий оптимальности в форме принципа максимума для задач оптимального импульсного управления [1].
3. Необходимые условия оптимальности в задаче (4)—(8) и их анализ
Обозначим через ![]() , где
, где ![]() исследуемый на оптимальность процесс задачи (4)—(8). Будем считать, что величина
исследуемый на оптимальность процесс задачи (4)—(8). Будем считать, что величина ![]() достаточно большая и на исследуемом процессе выполняется неравенство
достаточно большая и на исследуемом процессе выполняется неравенство 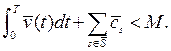 Выпишем условия принципа максимума [1], для простоты опуская черту у исследуемого процесса.
Выпишем условия принципа максимума [1], для простоты опуская черту у исследуемого процесса.
Функция Понтрягина:
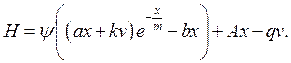 (10)
(10)
Соотношения для сопряженной переменной:
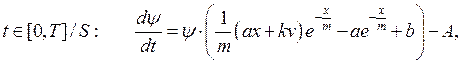 (11)
(11)
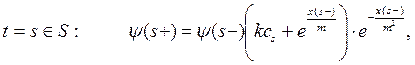 (12)
(12)
![]() (13)
(13)
Условия максимума:
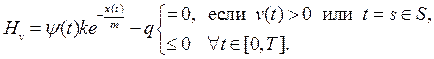 (14)
(14)
Условия оптимальности точек скачка:
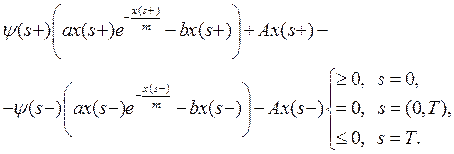 (15)
(15)
При записи соотношений (10)—(15) учли, что сопряженная переменная по ![]() тождественно равна
тождественно равна ![]() .
.
Прокомментируем условия принципа максимума.
1. Сопряженная функция ![]() является кусочно-непрерывной функцией. На участках, не содержащих точки множества
является кусочно-непрерывной функцией. На участках, не содержащих точки множества ![]() , она удовлетворяет дифференциальному уравнению (11), а в точках
, она удовлетворяет дифференциальному уравнению (11), а в точках ![]() — условию скачка (12) . В конечный момент времени выполняется условие трансверсальности (13).
— условию скачка (12) . В конечный момент времени выполняется условие трансверсальности (13).
2. Условие максимума управления (14) означает, что если ![]() ,
, ![]() — оптимальный процесс,
— оптимальный процесс, ![]() — соответствующая
— соответствующая ![]() сопряженная функция, то справедливо следующее:
сопряженная функция, то справедливо следующее:
· в моменты времени ![]() в которых
в которых ![]() выполняется равенство
выполняется равенство
![]()
· в моменты времени ![]() когда проводится обучение высокой интенсивности («агрессивное» обучение), выполняются равенства
когда проводится обучение высокой интенсивности («агрессивное» обучение), выполняются равенства
![]()
![]()
· в остальные моменты ![]() выполняется неравенство
выполняется неравенство
![]()
3. Условие оптимальности моментов времени, в которых осуществляется обучение высокой интенсивности, задается соотношениями (15).
Анализ условия принципа максимума приводит к следующим выводам:
1. Пусть выполняется условие:
![]() , (16)
, (16)
где ![]() и
и ![]() — решение следующей системы дифференциальных уравнений
— решение следующей системы дифференциальных уравнений


Тогда дополнительное обучение работников со стороны руководства фирмы не эффективно, т.е. ![]()
2. Пусть условие (16) не выполнено. Тогда существует магистральный участок ![]() , на котором
, на котором ![]() , где
, где ![]() и
и ![]() — решения уравнений
— решения уравнений
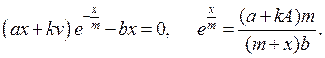 (17)
(17)
При этом реализуется один из следующих случаев:
2.1. Пусть ![]() . Тогда
. Тогда ![]() ,
, ![]()
Здесь ![]() – характеристическая функция отрезка
– характеристическая функция отрезка ![]() , а моменты выхода на магистраль
, а моменты выхода на магистраль ![]() и схода с нее
и схода с нее ![]() определяются из следующих условий:
определяются из следующих условий:
· момент ![]() :
: 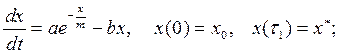
· момент ![]() :
:
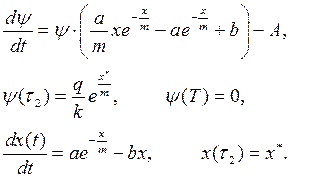
Таким образом, при ![]() из-за высокого начального уровня освоения новой технологии агрессивное обучение не эффективно. На начальном промежутке времени
из-за высокого начального уровня освоения новой технологии агрессивное обучение не эффективно. На начальном промежутке времени ![]() руководству фирму не выгодно прилагать усилия к обучению работников, однако, после снижении уровня
руководству фирму не выгодно прилагать усилия к обучению работников, однако, после снижении уровня ![]() до магистрального
до магистрального ![]() в момент
в момент ![]() проводится обычное обучение с интенсивностью
проводится обычное обучение с интенсивностью ![]() позволяющее поддерживать количество работников, владеющих новой технологией, на магистральном уровне.
позволяющее поддерживать количество работников, владеющих новой технологией, на магистральном уровне.
2.2. Пусть ![]() . Тогда
. Тогда
![]()
![]()

где момент схода с магистрального участка ![]() определяется как в 2.1. В этом случае в начальный момент времени эффективно проведение обучения высокой интенсивности, оно приводит к скачку функции
определяется как в 2.1. В этом случае в начальный момент времени эффективно проведение обучения высокой интенсивности, оно приводит к скачку функции ![]() в момент
в момент ![]() с начального уровня
с начального уровня ![]() до магистрального
до магистрального ![]() Далее проводится обычное обучение, нацеленное на сохранение магистрального уровня освоения новой технологии. После момента
Далее проводится обычное обучение, нацеленное на сохранение магистрального уровня освоения новой технологии. После момента ![]() затраты на обучение перестают окупаться.
затраты на обучение перестают окупаться.
2.3. В случае, когда горизонт планирования мал и ![]() магистральный участок может отсутствовать и управление будет чисто импульсным. При этом в начальный момент времени проводится обучение высокой интенсивности, поднимающее
магистральный участок может отсутствовать и управление будет чисто импульсным. При этом в начальный момент времени проводится обучение высокой интенсивности, поднимающее ![]() с начального уровня
с начального уровня ![]() до
до ![]() где
где ![]() удовлетворяет условиям
удовлетворяет условиям

В этом случае принципу максимума будет удовлетворять управление ![]() со следующими компонентами:
со следующими компонентами:
![]()
![]()
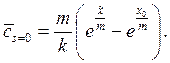
Проиллюстрируем полученные выводы на числовом примере. Зададим значения параметров
![]()
Вычислим магистральные значения уровней освоения новой технологии и усилий по обучению со стороны руководства фирмы из уравнений (17). Имеем
![]()
Поскольку ![]() то в начальный момент времени проводится «агрессивное» обучение, приводящее к скачкообразному увеличению уровня
то в начальный момент времени проводится «агрессивное» обучение, приводящее к скачкообразному увеличению уровня ![]() до магистрального. При этом
до магистрального. При этом ![]()
![]() Обычное обучение задается функцией
Обычное обучение задается функцией ![]() На Рис. 4 и 5 приведены графики управления и соответствующей траектории, удовлетворяющих принципу максимума. Можно показать, что для полученного процесса выполняются достаточные условия оптимальности из работы [2], и, следовательно, он является оптимальным.
На Рис. 4 и 5 приведены графики управления и соответствующей траектории, удовлетворяющих принципу максимума. Можно показать, что для полученного процесса выполняются достаточные условия оптимальности из работы [2], и, следовательно, он является оптимальным.
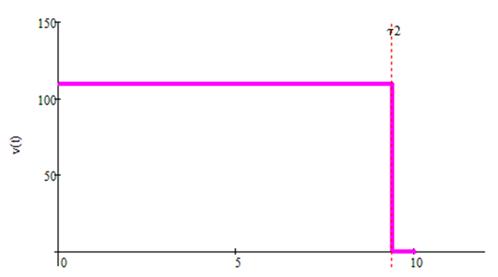
Рисунок 4. Оптимальное управление

Рисунок 5. Оптимальная траектория
Таким образом, в содержательных случаях решение задачи носит магистральный характер и имеет участок особого управления, на котором ![]() поддерживается на постоянном уровне
поддерживается на постоянном уровне ![]() . Если
. Если ![]() , то в начальный момент времени эффективно обучение с высокой интенсивностью, что приводит к скачкообразному возрастанию уровня
, то в начальный момент времени эффективно обучение с высокой интенсивностью, что приводит к скачкообразному возрастанию уровня ![]() до магистрального значения. Если
до магистрального значения. Если ![]() , то имеется начальный участок выхода на магистраль, на котором обучение не ведется.
, то имеется начальный участок выхода на магистраль, на котором обучение не ведется.
Список литературы:
1.Дыхта В.А., Самсонюк О.Н. Оптимальное импульсное управление с приложениями. М.: ФИЗМАТЛИТ, 2003.
2.Dykhta V.A., Samsonyuk O.N. Some applications of Hamilton-Jacobi inequalities for classical and impulsive optimal control problems // European Journal of Control. — 2011. — Vol. 17. — Pp. 55—69.
отправлен участнику


Оставить комментарий