ФУНКЦИЯ  РАСПРЕДЕЛЕНИЯ  ЗАРАБОТНОЙ  ПЛАТЫ ДОШКОЛЬНОГО,  ОБЩЕОБРАЗОВАТЕЛЬНОГО  И  ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО  ОБРАЗОВАТЕЛЬНОГО  УЧРЕЖДЕНИЙ ГОРОДА  САМАРЫ  В  СИСТЕМЕ  КРИВЫХ  ЛОРЕНЦА

Карпова  Ирина  Николаевна

студент  5  курса,  факультет  двигателей  летательных  аппаратов

СГАУ  имени  академика  С.П.  Королёва  (национальный  исследовательский  университет),  г.  Самара

Осипов  Александр  Иванович

научный  руководитель,  канд.  тех.  наук,  доцент  СГАУ  имени  академика  С.П.  Королёва  (национальный  исследовательский  университет),  г.  Самара

Одна  из  главных  задач  каждого  стабильного  государства  —  оптимальное  распределение  доходов  населения.  Данное  распределение  называется  кривой  Лоренца.  На  рис.  1  представлены  кривые  Лоренца  для  разных  стран  [1,  с.  55].

Рисунок  1.  Кривые  Лоренца  для  Англии,  Швеции,  Бразилии,  США,  России,  «Золотого  сечения»  и  «Абсолютного  равенства»  доходов

Методика  нахождения  идеальной  кривой  Лоренца  может  быть  построена  на  использовании  правила  «Золотого  сечения».  Если  кривая  Лоренца  представляет  собой  график  вида  у=хⁿ,  то  по  данным  работы  [1,  с.  56]  n_з.с.=1,618.

Пусть  кривая  Лоренца  показывает,  какую  часть  совокупной  заработной  платы  учреждения  получает  каждая  доля  высокооплачиваемых  и  низкооплачиваемых  сотрудников.

По  оси  абсцисс  укажем  относительный  табельный  номер  сотрудника:

х_i=i/m  (1)

где:  m  —  число  сотрудников;

i  —  табельный  номер.

По  оси  ординат  укажем  накопительную  относительную  заработную  плату  сотрудников  —  функцию  распределения:

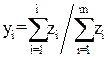  (2)

где:    —  заработная  плата  сотрудников  с  номером  i  в  порядке  возрастания.

Очевидно,  что  чем  ближе  функция  распределения  к  диагонали  —  «Абсолютному  равенству»,  тем  равномернее  распределена  заработная  плата  среди  сотрудников  (Рис.  1).  Нахождения  коэффициента  эластичности  (показателя  степени)  функции  распределения  заработной  платы  для  каждого  учреждения  (детский  сад,  школа,  кафедра  университета)  проведём  с  помощью  логарифмирования  х  и  у:

n_i=Lgy_i/Lgx_i  (3)

  и  осреднения  результатов  [1,  с.  57]: 

n_ср.=  Σn_i/m,  (4)

где:  —  коэффициент  эластичности  (показатель  степени).

Проанализируем  данные  для  кафедры  университета  (Рис.  2)  по  предлагаемой  методике  (Табл.  1.).

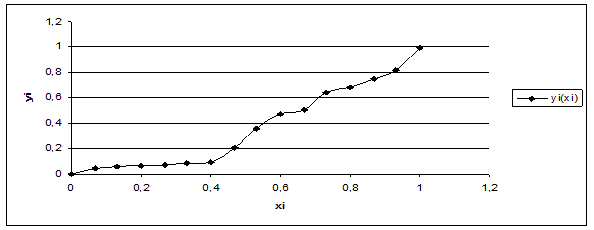
Рисунок  2.  Исходные  данные  для  кафедры  университета

Таблица  1.

Распределение  относительной  заработной  платы  работников  на  кафедре  университета

С  помощью  добавления  линии  тренда  на  диаграмму  рис.  3  в  среде  «MS  Excel»  мы  также  можем  получить  уравнение  вида  ,  где  коэффициент  n  при  Lgx  является  показателем  степени  функции  распределения  на  рис.  2  n₁=1,71.  По  данным  регрессионного  анализа  величина  достоверности  аппроксимации  достаточно  значительная:  коэффициент  детерминации  R²=0.856  (Рис.  3).

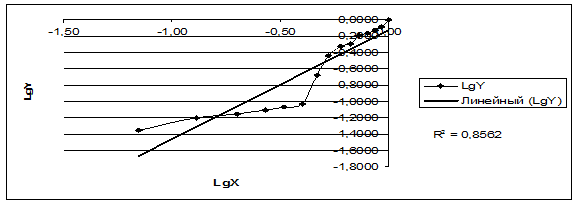
Рисунок  3.  Определение  показателя  степени  функции  распределения  зарплаты  для  кафедры  университета

На  рис.  4  видно,  что  для  кафедры  университета  теоретические  значения  (y_т=х^1.71)  неплохо  совпадают  с  исходными  данными  (у),  из  чего  можно  сделать  вывод,  что  выбранная  степенная  функция  хорошо  описывает  функцию  распределения  заработной  платы.

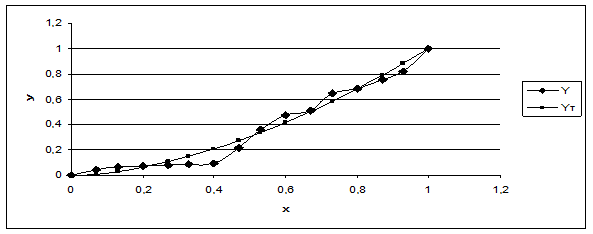
Рисунок  4.  Функция  распределения  заработной  платы  на  кафедре  университета

Вид  y=xⁿ  функции  распределения  заработной  платы  носит  универсальный  характер  и  может  быть  использован  при  оценке  дифференциации  доходов  любого  учреждения,  так  как  переменные  х  и  у  являются  относительными.  Зная  лишь  одно  экспериментальное  значение  и  эластичность  кривой,  можно  построить  распределение  заработной  платы  всего  учреждения.

Для  проверки  универсальности  вида  функции  распределения  рассмотрим  данные  по  заработной  плате  в  детском  саду  (Рис.  5).

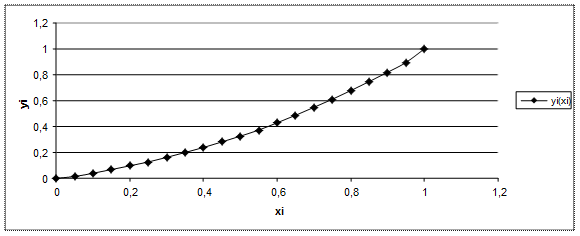
Рисунок  5.  Исходные  данные  для  детского  сада

Здесь  по  результатам  регрессионного  анализа  коэффициент  эластичности  равен  n₂=1.55.  Следует  отметить,  что  полученная  степенная  функция  y_т=x^1.55  очень  точно  (R²=0.998)  описывает  распределение  исходных  данных. 

Аналогично  рассмотрим  распределение  заработной  платы  в  школе  (Рис.  6).

Рисунок  6.  Исходные  данные  для  школы

В  этом  случае  по  данным  регрессионного  анализа  (величина  достоверности  аппроксимации:  R²=0.988)  коэффициент  эластичности  n₃=1.87.  Для  школы  теоретическое  значение  функции  распределения  у_т=х^1.87  хорошо  совпадает  с  экспериментальным,  из  чего  можно  сделать  вывод,  что  выбранный  степенной  вид  функции  и  в  этом  случае  точно  описывает  закон  распределения  заработной  платы  [2,  с.  591].

Проанализировав  на  рис.  7  показатели  степени  функции  распределения  доходов  населения  разных  стран,  а  также  функции  распределение  зарплаты  в  рассматриваемых  учреждениях,  можно  придти  к  выводу,  что  в  целом  заработные  платы  в  образовательных  учреждениях  города  Самары  имеют  более  равномерное  распределение,  чем  в  целом  по  Российской  Федерации.

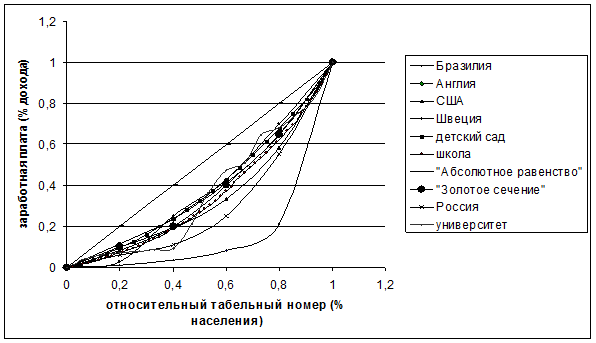
Рисунок  7.  Функция  распределения  доходов

В  результате  работы  была  определена  (Рис.  8)  вероятностная  плотность  функции  распределения  доходов  европейских  стран  и  зарплаты  исследуемых  образовательных  учреждений  города  Самары  (Табл.  1)  по  формуле

f(x)=dy/dx=(d/dx)_*xⁿ=nx^n-1  (5)

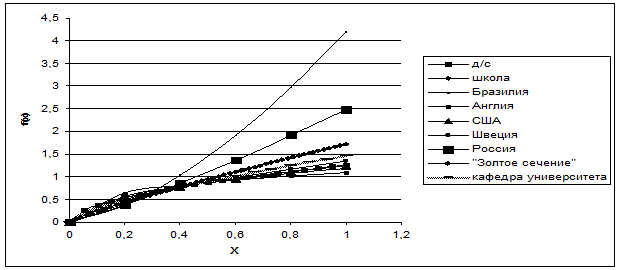
Рисунок  8.  Вероятностная  плотность  функции  распределения

Выводы:

·     Предложена  методика  нахождения  функция  распределения  заработной  платы  для  ряда  учреждений  города  Самары.

·     Обнаружена  близость  кривых  Лоренца  распределения  доходов  работников  в  США  (n_сша=1.51)  и  детского  сада  (n₂=1.55). 

·     Распределение  зарплаты  работников  школы  (n₃=1.87)  ближе  расположено  к  «золотому  сечению»  (n_з.с.=1.618).

·       Распределение  зарплаты  сотрудников  кафедры  университета  занимает  среднее  положение  между  кривыми  детского  сада  и  школы:  n₃=  (n₁+  n₂)/2.

·     Впервые  введена  в  рассматриваемом  анализе  функция  распределения  заработной  платы  и  её  плотность.

Список  литературы:

1.Медведко  В.А.,  Осипов  А.И.  Модель  государственного  управления  распределением  доходов  населения/  Альянс  наук:  вчений  вченому:  матерiали  VI  Мiжнар.  наук.-практ.  конф.,  25—26  лют.  2011  р.  :  У  8  т.  Днепропетровск:  Бiла  К.О.,  2011.  Т.  1:  Державне  управлiння.  —  2011.  —  80  с.  —  с.  55—64. 

2.Karpova  I.N.,  Osipov  A.I.,  Municipal  establishments  the  salary  distribution  method  in  the  Lorenz’s  curves  system/  European  Science  and  Technology  [Text]:  materials  of  the  IV  international  research  and  practice  conference,  Vol.  I,  Munich,  April  10th  —  11th,  2013  /  publishing  office  Vela  Verlag  Waldkraiburg  Munich  Germany,  2013  —  776  p.  —  р.  586—593.