ОПРЕДЕЛЕНИЕ ПРОГНОЗНОЙ ЦЕНЫ НА МЕДЬ

Фокина Мария Сергеевна

магистрант 2 курса, кафедра вычислительной математики и информатики ЮУрГУ, г. Челябинск

E-mail: f.mariya.s1988@gmail.ru

Латипова Алина Таиховна

научный руководитель, канд. физ.-мат. наук, доцент ЮУрГУ, г. Челябинск

Рассмотрим цены на медь за 2009—2011 гг.

Таблица 1.

Котировки меди

По данным таблицы 1 построим график. Как видно из графика, наблюдается тенденцию к увеличению цен на медь.

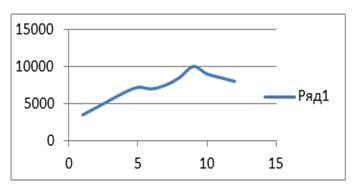
Рисунок 1. Котировки меди в 2009—2011 гг.

Таблица 2.

Данные для расчета тренда

Используя систему нормальных уравнений

определим коэффициенты и получим уравнение тренда:

Таблица 3.

Определение сезонной компоненты

Проверим качество нашего полученного уравнения регрессии. Для этого определим ошибку аппроксимации.

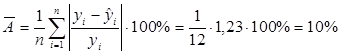
Ошибка аппроксимации в пределах нормы.

Рассчитаем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции.

Можно сделать вывод, что линейная связь между переменными сильная.

Найдем коэффициент детерминации. . Регрессия хорошо аппроксимирует статистические данные, так как коэффициент детерминации близок к 1.

Проверим значимость коэффициента уравнения регрессии. Для того, чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции нормальной случайной величины при конкурирующей гипотезы H₁≠0, надо вычислить наблюдаемое значение критерия:

Мы получили расчетный коэффициент Стьюдента>3, таким образом, сделаем вывод о полной гарантии коэффициентов уравнения регрессии.По таблице Стьюдента при коэффициенте значимости α=0,05 и степенями свободы k=10, t_табл.=2,228. Следовательно, оснований отвергать гипотезу нет.

Оценим сезонную составляющую аддитивной модели как разность между фактическими котировками и значениями тренда. Оценки сезонной компоненты представлены в 4 столбце таблицы 3. Оценим сезонную компоненту мультипликативной модели как отношение фактических значений котировок меди к значениям тренда. Результаты вычислений представлены в последнем столбце таблицы 3.

Полученные оценки сезонной компоненты пока еще непригодны для построения прогнозов, так как они показывают сезонные отклонения от тренда для конкретного периода времени в исходном ряду. Для того, чтобы оценки сезонности можно было использовать в целях получения более точного прогноза, скорректированного с учетом сезонных изменений, необходимо найти средние оценки сезонной компоненты.

Рассмотрим аддитивную модель. Найдем средние оценки по кварталам:

В моделях с сезонной компонентой предполагается, что сезонные воздействия за период взаимопогашаются, т. е. сумма значений сезонных компонент должна быть равна нулю. Проверим данное утверждение для нашей модели.

450–77,87–205,73–166,9 = –0,5.

Определим корректирующий коэффициент: k= –0,5/4= –0,125

Скорректированные значения сезонной компоненты рассчитываются как разность между ее средней оценкой и корректирующим коэффициентом k. Для первого квартала: 450+0,125= 450,125; для второго квартала: –77,87–(–0,125)= –77,745; для третьего: –205,73–(–0,125)= –205,605; для четвертого: –166,9 –(–0,125)= –166,775.

Проверим условие равенства нулю суммы скорректированных значений: 450,125–77,745–205,605–166,775=0.

Таким образом, полученные значения сезонной компоненты рассчитаны верно, и они могут использоваться в аддитивной модели прогноза.

Найдем прогноз на 2012 г. с учетом сезонной компоненты:

y₁₃=4144+461,2*13+450,125=10590;

y₁₄=4144+461,2*14-77,745=10523;

y₁₅=4144+461,2*15-205,605=10856;

y₁₆=4144+461,2*16-166,775=11356;

Рассмотрим мультипликативную модель:

Найдем сумму данных сезонных компонент: 1,027+0,976+0,98+1=3,98.

В нашем случае периодичность сезонных колебаний — 4, следовательно, корректирующий коэффициент не близок к 1: 4/3,98=1

Скорректированные значения сезонной компоненты или индексы сезонности равны произведению средних оценок и корректирующего коэффициента. В нашем примере индексы сезонности не претерпят существенные изменения, поскольку корректирующий коэффициент близок к 1. Полученные значения индексов сезонности могут использоваться в моделях прогноза.

Список литературы:

1.Ломкова Е.Н. Экономико-математические модели управления производством: учебное пособие / Е.Н. Ломкова, А.А. Эпов. — Волгоград: РПК «Политехник», 2005 г.

2.Дуброва Т.А. Статистическе методы прогнозирования: учебное пособие / Т.А. Дуброва — Москва: ЮНИТИ-ДАНА, 2003. — 206 с.

3.Информация о финансовых рынках [Электронный ресурс] — Режим доступа. — URL: http://www.finam.ru (03.01.2013 г).