Статья опубликована в рамках: VI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ЭКОНОМИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 20 декабря 2012 г.)
Наука: Экономика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОПТИМИЗАЦИЯ РЕКЛАМНЫХ РАСХОДОВ В МОДЕЛИ С ПРОМЕЖУТОЧНЫМ КОНТРОЛЕМ ЭФФЕКТИВНОСТИ РЕКЛАМЫ
Седых Анна Николаевна
студент кафедры «Методы оптимизации» ИМЭИ ИГУ, г. Иркутск
E-mail: Seanni_92@mail.ru
Самсонюк Ольга Николаевна
научный руководитель, канд. физ.-мат. наук, старший научный сотрудник ИДСТУ СО РАН, г. Иркутск
1. Описание модели оптимизации рекламных расходов
В статье рассматривается модель рационального расходования средств на рекламу. В основе модели лежит известная задача оптимального управления рекламной стратегией фирмы [2], она дополнена промежуточным фазовым ограничением, имеющим смысл контроля объема продаж в заданный момент времени. Кроме того, допускается возможность проведения агрессивной рекламной компании, при которой большие рекламные расходы осуществляются в течение кратких промежутков времени, что приводит к резким, почти скачкообразным увеличениям объемов продаж. Допустимость агрессивной рекламы и наличие промежуточного фазоограничения существенно усложняют базовую модель и приводят к задаче оптимального управления с разрывными траекториями. Модель описывается следующими соотношениями:
![]() (1)
(1)
![]() (2)
(2)
![]()
![]() (3)
(3)
![]() (4)
(4)
Здесь ![]() — доля рынка товара, которую контролирует фирма в момент
— доля рынка товара, которую контролирует фирма в момент ![]() ,
, ![]() — текущие затраты на рекламу,
— текущие затраты на рекламу, ![]() — коэффициент, характеризующий эффективность расходов на рекламу,
— коэффициент, характеризующий эффективность расходов на рекламу, ![]() и
и ![]() — коэффициенты дисконтирования и забывания соответственно,
— коэффициенты дисконтирования и забывания соответственно, ![]() — прибыль, получаемая при охвате всех потенциальных покупателей товара,
— прибыль, получаемая при охвате всех потенциальных покупателей товара, ![]() — контрольный момент времени,
— контрольный момент времени, ![]() — наименьший желаемый охват рынка в момент
— наименьший желаемый охват рынка в момент ![]() ,
, ![]() — горизонт планирования.
— горизонт планирования.
Уравнение динамики (2) имеет следующую интерпретацию: слева стоит мгновенный прирост объема продаж товара, изменение которого обусловлено двумя факторами. Во-первых, часть населения, информированного через рекламу о продукции фирмы, забывает об этом, или отказывается от услуг фирмы, или покидает рынок по каким-то причинам с постоянным темпом забывания ![]() . Во-вторых, прирост объемов продаж пропорционален текущим рекламным вложениям, эффективность которых характеризуется коэффициентом
. Во-вторых, прирост объемов продаж пропорционален текущим рекламным вложениям, эффективность которых характеризуется коэффициентом ![]() , а также части рынка, пока не охваченной фирмой, но потенциально ей доступной. Управление
, а также части рынка, пока не охваченной фирмой, но потенциально ей доступной. Управление ![]() удовлетворяет ограничениям (3), т. е. текущие рекламные расходы неотрицательны, а суммарные за весь промежуток времени не превышают заранее заданной суммы
удовлетворяет ограничениям (3), т. е. текущие рекламные расходы неотрицательны, а суммарные за весь промежуток времени не превышают заранее заданной суммы ![]() . Цель управления состоит в максимизации критерия качества (1), имеющего смысл суммарной прибыли за планируемый период времени. Промежуточное ограничение (4) задает нижнюю границу уровня продаж в контрольный момент времени
. Цель управления состоит в максимизации критерия качества (1), имеющего смысл суммарной прибыли за планируемый период времени. Промежуточное ограничение (4) задает нижнюю границу уровня продаж в контрольный момент времени ![]() .
.
Основная особенность задачи (1)—(4) состоит в том, что значение управление неограниченно сверху и теоретически может быть бесконечно большим. С экономической точки зрения это означает, что допускается агрессивная реклама, при которой в течение очень коротких промежутков времени осваиваются значительные суммы денег, что приводит к резкому, почти скачкообразному увеличению объема продаж. Из-за неограниченности понтрягинского множества управлений задача оптимального управления (1)—(4) не имеет решения в классе абсолютно непрерывных траекторий ![]() и измеримых ограниченных управлений
и измеримых ограниченных управлений ![]() Отметим, что произвольная последовательность траекторий системы (2), (3) будет иметь равномерно ограниченные полные вариации на отрезке [
Отметим, что произвольная последовательность траекторий системы (2), (3) будет иметь равномерно ограниченные полные вариации на отрезке [![]() , и, следовательно, все ее частичные поточечные пределы являются функциями ограниченной вариации. Таким образом, задача (1)—(4) может быть рассмотрена в расширенной постановке с разрывными траекториями и импульсными управлениями (мерами Лебега-Стилтьеса). В дальнейшем будем предполагать, что множество моментов времени, в которых фирма проводит агрессивную рекламу, конечно, а между этими моментами может осуществляться обычная реклама, описываемая функцией
, и, следовательно, все ее частичные поточечные пределы являются функциями ограниченной вариации. Таким образом, задача (1)—(4) может быть рассмотрена в расширенной постановке с разрывными траекториями и импульсными управлениями (мерами Лебега-Стилтьеса). В дальнейшем будем предполагать, что множество моментов времени, в которых фирма проводит агрессивную рекламу, конечно, а между этими моментами может осуществляться обычная реклама, описываемая функцией ![]()
Приведем адаптированную формулировку необходимых условий оптимальности в форме принципа максимума задачи оптимального управления с траекториями ограниченной вариации при наличии промежуточных ограничений [1].
2.Постановка задачи оптимального импульсного управления с промежуточными фазоограничениями. Принцип максимума
Приведем частную постановку задачи оптимального импульсного управления, в которой траектории являются кусочно абсолютно непрерывными функциями с конечным числом скачков. Вначале опишем множество импульсных управлений и соответствующих им траекторий.
Импульсное управление: Будем рассматривать импульсное управление следующего вида

с компонентами, удовлетворяющими условиям
![]()
(5)

Здесь
· ![]() — конечное множество точек отрезка [
— конечное множество точек отрезка [![]() , в которых сосредоточена дискретная составляющая меры
, в которых сосредоточена дискретная составляющая меры ![]() ;
;
· ![]() — точка импульса (точка скачка траектории);
— точка импульса (точка скачка траектории);
· ![]() — интенсивность импульса в момент
— интенсивность импульса в момент ![]() ;
;
· ![]() — измеримая существенно ограниченная функция,
— измеримая существенно ограниченная функция, ![]() ;
;
· ![]() — дельта функция Дирака, сосредоточенная в точке
— дельта функция Дирака, сосредоточенная в точке ![]() .
.
Траектория, соответствующая импульсному управлению ![]() и начальному условию
и начальному условию ![]() — это кусочно абсолютно непрерывная функция
— это кусочно абсолютно непрерывная функция ![]() ,
, ![]() ,
, ![]() которая на участках абсолютной непрерывности удовлетворяет уравнению:
которая на участках абсолютной непрерывности удовлетворяет уравнению:
![]() (6)
(6)
а в точках импульса ![]() – условию скачка
– условию скачка
![]() , (7)
, (7)
где функция ![]() — решение системы дифференциальных уравнений (называемой предельной)
— решение системы дифференциальных уравнений (называемой предельной)
![]() , (8)
, (8)
в которой функция ![]() и число
и число ![]() удовлетворяют условиям:
удовлетворяют условиям:
![]() (9)
(9)
![]() . (10)
. (10)
Заметим, что условиям (9), (10) может удовлетворять не единственная пара ![]() , следовательно, заданным управлению
, следовательно, заданным управлению ![]() и начальному условию
и начальному условию ![]() может соответствовать множество траекторий, причем индивидуальная траектория выделяется из этого множества при помощи набора
может соответствовать множество траекторий, причем индивидуальная траектория выделяется из этого множества при помощи набора ![]() . Обозначим этот набор через
. Обозначим этот набор через ![]() и назовем его предельным управлением. Таким образом, управлению
и назовем его предельным управлением. Таким образом, управлению ![]() и начальному условию
и начальному условию ![]() соответствует единственная траектория
соответствует единственная траектория ![]() , определенная соотношениями (6)-(10).
, определенная соотношениями (6)-(10).
Назовем импульсным процессом тройку ![]() , состоящую из импульсного управления, предельного управления и соответствующей траектории. Будем называть импульсный процесс
, состоящую из импульсного управления, предельного управления и соответствующей траектории. Будем называть импульсный процесс ![]() допустимым, если его траекторная компонента удовлетворяет промежуточному ограничению
допустимым, если его траекторная компонента удовлетворяет промежуточному ограничению
![]()
в нефиксированный момент времени ![]() и терминальному ограничению
и терминальному ограничению
![]() ,
,
где: ![]() — заданные вектор-функции.
— заданные вектор-функции.
Обозначим через ![]() множество всех допустимых импульсных процессов.
множество всех допустимых импульсных процессов.
Рассмотрим задачу ![]() минимизации функционала
минимизации функционала ![]() на множестве
на множестве ![]() , т. е.
, т. е.
![]()
Будем предполагать, что функции ![]() непрерывно дифференцируемы, а матричная функция
непрерывно дифференцируемы, а матричная функция ![]() непрерывно дифференцируема и удовлетворяет условию роста по переменной
непрерывно дифференцируема и удовлетворяет условию роста по переменной ![]() .
.
Обозначим через ![]() исследуемый на оптимальность процесс, а через
исследуемый на оптимальность процесс, а через ![]() и
и ![]() —
— ![]() и
и ![]() соответственно. Выпишем адаптированные к постановке задачи
соответственно. Выпишем адаптированные к постановке задачи ![]() необходимые условия оптимальности в форме принципа максимума из [1].
необходимые условия оптимальности в форме принципа максимума из [1].
Функция Понтрягина: ![]()
где: ![]() .
.
Функция Лагранжа: ![]() ,
,
где: ![]()
![]() .
.
Теорема 1. Пусть ![]() оптимальный процесс задачи
оптимальный процесс задачи ![]() . Тогда найдутся такие
. Тогда найдутся такие
· числа ![]() ,
, ![]() ,
,
· кусочно абсолютно непрерывные функции ![]() ,
,
· абсолютно непрерывные функции ![]() , определенные для каждого момента
, определенные для каждого момента ![]() ,
,
что выполняются условия:
1. условия неотрицательности, нетривиальности и дополняющей нежесткости:
![]()
![]() ;
;
2. функции ![]() на интервалах абсолютной непрерывности удовлетворяют сопряженной дифференциальной системе
на интервалах абсолютной непрерывности удовлетворяют сопряженной дифференциальной системе
![]() ;
;
для каждого ![]() функции
функции ![]() удовлетворяют сопряженным предельным системам на отрезке [
удовлетворяют сопряженным предельным системам на отрезке [![]()
![]() ;
;
3. условия скачка в точках импульса и промежуточной точке:
(а) в точках ![]()
![]()
![]()
(б) в промежуточной точке ![]() , принадлежащей
, принадлежащей ![]() ,
,
![]() ,
,
![]()
(в) в промежуточной точке ![]() , не принадлежащей
, не принадлежащей ![]() ,
,
![]() ,
,
![]() ;
;
4. условие трансверсальности:
![]() ;
;
5. условия максимума компоненты управления ![]() :
:
![]()
![]() ;
;
6. условия максимума предельного управления (и, следовательно, компонент управления ![]() ):
):
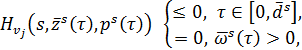
![]() ,
, ![]()
7. условия оптимальности моментов импульса и промежуточного момента:
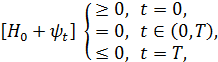
где:
![]()
В следующем параграфе применим выписанный принцип максимума к анализу задачи оптимизации рекламных расходов. Заметим, что в данной задаче управление скалярное. Последнее упрощает условия принципа максимума, так как в этом случае вводить предельное управление необязательно (см. [2]) и в наборе ![]() можно положить
можно положить ![]() .
.
3. Постановка и анализ задачи оптимизации расходов на рекламу с разрывными траекториями
Приведем постановку задачи оптимизации рекламных расходов, допускающую агрессивную рекламу, приводящую к скачку в объема продаж. Вначале приведем задачу (1)—(4) с интегральным функционалом к задаче с терминальным, положив ![]() . Теперь опишем множество допустимых процессов с разрывными траекториями и критерий качества в расширенной постановке задачи.
. Теперь опишем множество допустимых процессов с разрывными траекториями и критерий качества в расширенной постановке задачи.
Импульсное управление:

с компонентами, удовлетворяющими условиям
![]()
(11)

Здесь
· ![]() — конечное множество точек отрезка [
— конечное множество точек отрезка [![]() , в которых проводится агрессивная реклама;
, в которых проводится агрессивная реклама;
· ![]() интерпретируется как сумма денег, затраченная на агрессивную рекламу в момент времени
интерпретируется как сумма денег, затраченная на агрессивную рекламу в момент времени ![]() ;
;
· ![]() описывает интенсивность обычных рекламных расходов, т. е. не приводящих к скачкам продаж,
описывает интенсивность обычных рекламных расходов, т. е. не приводящих к скачкам продаж, ![]() ;
;
Интегральное ограничение в (11) интерпретируется как ограничение на общие суммарные расходы как на обычную рекламу, так и на агрессивную.
Траектория, соответствующая импульсному управлению ![]() , состоит из кусочно абсолютно непрерывных функций
, состоит из кусочно абсолютно непрерывных функций ![]() , возможно имеющих скачки на концах отрезка [0,T]. На участках абсолютной непрерывности они удовлетворяют дифференциальным уравнениям
, возможно имеющих скачки на концах отрезка [0,T]. На участках абсолютной непрерывности они удовлетворяют дифференциальным уравнениям
![]()
![]()
а в моменты проведения агрессивной рекламы ![]() — условиям скачка
— условиям скачка
![]() .
.
Допустимые траектории удовлетворяют промежуточному условию
![]() .
.
Критерий качества рекламной политики:
![]() (следовательно,
(следовательно, ![]() ).
).
Выпишем условия принципа максимума для поставленной задачи в соответствии с п. 2.
Функция Понтрягина ![]() .
.
Функция Лагранжа ![]() .
.
Обозначим через ![]() искомый, исследуемый на оптимальность процесс, а через
искомый, исследуемый на оптимальность процесс, а через ![]() и
и ![]() —
— ![]() и
и ![]() соответственно (для простоты в дальнейшем будем опускать черту у искомого процесса). Тогда условия теоремы 1 принимают следующий вид: найдутся такие
соответственно (для простоты в дальнейшем будем опускать черту у искомого процесса). Тогда условия теоремы 1 принимают следующий вид: найдутся такие
· числа ![]() ,
,
· кусочно абсолютно непрерывные функции ![]() ,
,
· абсолютно непрерывные функции ![]() , определенные для каждого момента
, определенные для каждого момента ![]() , что выполняются условия:
, что выполняются условия:
(1) условия неотрицательности, нетривиальности и дополняющей нежесткости: ![]() ;
;
(2) сопряженная система:
![]()
![]()
предельная сопряженная система:
![]() ;
;
(3) условия скачка сопряженных функций в моменты импульса и в промежуточной точке:
(а) в точках ![]()
![]() ,
,
(б) в промежуточной точке ![]() , принадлежащей
, принадлежащей ![]() ,
,
![]()
(в) в промежуточной точке ![]() , не принадлежащей
, не принадлежащей ![]() ,
,
![]() ;
;
(4) условие трансверсальности:
![]() ;
;
(5) условие максимума по абсолютно непрерывной составляющей ![]() :
:
![]()
(6) условие максимума по дискретной составляющей управления в точках ![]() :
:
![]() ,
, ![]() ,
,
![]() ;
;
![]() ,
, ![]() ,
,
![]() ;
;
(7) условие оптимальности моментов импульса:
а) при ![]()
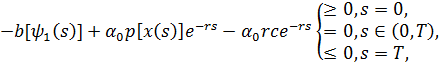
б) если ![]() принадлежит
принадлежит ![]() , то выполняется равенство
, то выполняется равенство
![]()
в) если ![]() не принадлежит
не принадлежит ![]() , то выполняется равенство
, то выполняется равенство
![]() .
.
Анализ условий принципа максимума и обоснование существования решения в рассматриваемом классе процессов позволяют получить оптимальное решение задачи. Приведем оптимальное управление для двух наиболее интересных случаев с наличием магистрального участка. В первом случае агрессивная реклама проводится в начальный и промежуточный (контрольный) моменты времени
![]()
![]()
Во втором — только в контрольный момент, так как уровень начального объема продаж превышает магистральный
![]()
![]()
Здесь ![]() — магистральное значение уровня продаж, определяется как решение уравнения
— магистральное значение уровня продаж, определяется как решение уравнения
![]()
![]() — характеристическая функция множества A.
— характеристическая функция множества A.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, проект № 12-01-31252, и ФЦП «Научные и научно-педагогические кадры инновационной России», соглашение 8211 от 6.08.2012.
Список литературы:
1.Дыхта В.А., Самсонюк О.Н. Принцип максимума для гладких задач оптимального импульсного управления с многоточечными фазоограничениями [Текст] / Дыхта В.А., Самсонюк О.Н. Журн. вычисл. матем. и матем. физики. 2009. Т. 49, № 6. С. 981—997.
2.Sethi S.P., Thomsom G.L. Optimal control theory. Applications to management science USA [Текст] / S.P. Sethi, G.L. Thomsom. Boston,1981.
дипломов


Оставить комментарий