ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ЭКОСИСТЕМЫ ЖЕРТВА - ХИЩНИК

Абрамов Александр

класс 11 «Т», МАОУ «Лицей города Троицка», Москва, городской округ Троицк

научный руководитель: Куркина Любовь Григорьевна

педагог высшей категории, преподаватель информатики,

МАОУ «Лицей города Троицка», Москва, городской округ Троицк

научный руководитель: Таран Татьяна Владимировна

педагог высшей категории, канд. физ.-мат. наук,

преподаватель математики, МАОУ «Лицей города Троицка»,

Москва, городской округ Троицк

Математическое моделирование динамики биологических популяций актуальная и очень интересная проблема, так как позволяет выявить некоторые закономерности в развитии биологических объектов (живых организмов) математическими методами.

В настоящей работе представлены результаты численного исследования простой экосистемы  жертва — хищник. Предполагалось, что экосистема состоит из кроликов (жертв), для которых имеется неограниченный запас пищи (травы), и лис (хищников), которые для пропитания охотятся за кроликами, являющихся единственной пищей для лис. Классическая математическая модель, принадлежащая Вольтерра [2],  описывает эту систему двумя нелинейными дифференциальными уравнениями первого порядка:

,

c начальными условиями   ,   . Здесь  — время,  — число кроликов,  — число лис,  — положительная константа. При   популяции кроликов и лис не взаимодействуют, и кролики активно размножаются, а лисы вымирают от голода. При  лисы встречают кроликов с вероятностью, пропорциональной произведению тех и других. В результате таких встреч число кроликов убывает, а число лис возрастает.

Для решения данной системы дифференциальных уравнений использовался метод прогноза и коррекции [1]. Интервал времени разбивался на промежутки с шагом  и на старте (на первом шаге по времени) для вычисления  и  использовался  метод Эйлера:

После этого применялся собственно метод прогноза и коррекции, а именно, для

 значения  и    находились (предсказывались) с помощью формул:

Здесь верхний индекс  означает исходное приближение к  и  соответственно, т.е. предсказанное значение. Затем производилась коррекция значений  и , при этом  - ые  приближения к   и   вычислялись по формулам:

Итерационный процесс прекращался, когда выполнялись условия:

здесь  — малое положительное число.

Оценки ошибки округления выводились на печать и использовались для учёта окончательной поправки в значениях  x и y согласно формуле:

,

.

Вычислительная программа, реализующая изложенный метод, написана на языке программирования Паскаль. Графическая обработка полученных результатов производилась с использованием возможностей программы Excel.

Система дифференциальных уравнений решалась при различных  начальных условиях и значениях параметра. При  и различных  и  были получены периодические решения. Это соответствует циклическому закону Вольтерра, который выяснил, что с какой бы численности жертвы и хищники ни стартовали —  или  — динамическая экосистема будет возвращаться к этим же начальным условиям, пройдя определенный замкнутый цикл. На рис.1 приведена фазовая диаграмма системы «хищник — жертва» для трёх различных начальных значений. 

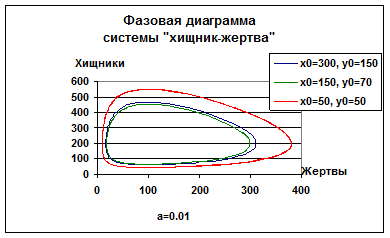
Рисунок 1. Фазовая диаграмма системы «хищник — жертва» для трёх различных начальных значений

Дадим интерпретацию полученного циклического результата. Если система жертва-хищник стартовала, например, из точки  с координатами  то увеличение численности кроликов приводит к увеличению численности лис (движемся по кривой против часовой стрелки). Эта тенденция сохраняется до некоторой «правой» точки, после чего численность лис продолжает увеличиваться, а численность кроликов начинает уменьшаться. В некоторой точке «сверху» возникает ситуация, когда хищников становится так много, что они поедают жертву еще до того, как она оставила потомство. Число кроликов убывает; возникает ситуация, когда лиса, не найдя добычи, погибает. Поэтому на участке от точки «сверху» до некоторой точки «слева» наблюдается спад численности и хищника, и жертвы. Здесь хищников становится так мало, что кролики начинают размножаться по законам, определяемым параметром  и коэффициентом  в соответствующем дифференциальном уравнении. Увеличение численности кроликов приводит к увеличению численности лис —  постепенно начинает восстанавливаться ситуация, с которой начался цикл.

На рис.2  изображён график, из которого видно, что число лис достигает максимального уровня с периодичностью 5 лет. Сходные колебания испытывает популяция кролика, причем максимальные значения его плотности наступают в среднем на год раньше, чем у лисы. Корреляция между численностью лис и кроликов подтверждает правильность модели Вольтерра жертва-хищник.

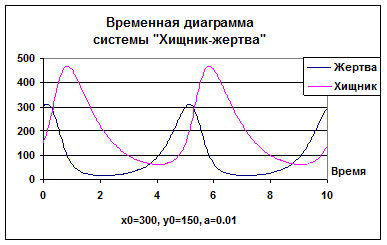
Рисунок 2. Временная диаграмма системы «хищник — жертва»

Интересный результат получается при  когда число кроликов становится меньше единицы (Рис.3). Это можно интерпретировать как то, что кролики вымирают. При  наблюдается вымирание лис (Рис.4).

Таким образом, мы убедились, что даже простая математическая модель достаточно хорошо описывает сложную биологическую систему: долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Отметим, что математическую модель Вольтерра можно использовать и для изучения других динамических систем, где есть конкурирующие объекты (в физике, социологии, экономике).

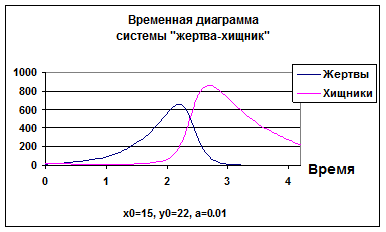
Рисунок 3. Временная диаграмма системы «хищник — жертва»

при x₀  = 15, y₀  = 22 (наблюдается вымирание кроликов (жертв))

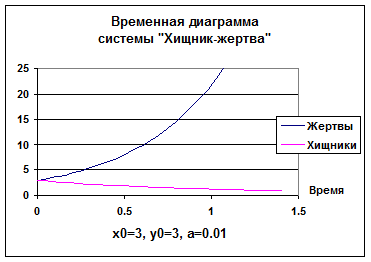
Рисунок 4. Временная диаграмма системы «хищник — жертва»

при x₀ = y₀ = 3 (наблюдается вымирание лис (хищников))

Список литературы:

1.Мак-Кракен Д., Дорн У. Численные методы и программирование на фортране. – М.: Мир, 1977. — 584 с.

2.Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. — М.: Мир, 1980. — 279 с.