ИССЛЕДОВАНИЕ RLC-КОНТУРА

Тихонов Владимир

класс 11 «Б», ОПШМТ № 11, г. Павлодар

Гордова Наталья Владимировна

научный руководитель, преподаватель физики, ОПШМТ № 11, г. Павлодар

E-mail: etih@yandex.ru

 

Введение

Интерес, проявляемый в настоящее время к колебатель­ным процессам, весьма широк и далеко выходит за пределы изучения качаний маятника, как это было в начале XVII века, когда ученые только начали интересоваться колебаниями.

По современным представлениям науки звуковые, тепловые, световые, электромагнитные явления, т. е. важнейшие фи­зические процессы окружающего нас мира, являются раз­личными видами колебаний. Они играют исключительную роль в таких веду­щих отраслях техники, как электричество и радио.

Выработка, передача и потребление электрической энергии, телефония, телеграфия, радиовещание, радиолокация — все эти важные и сложные отрасли техники основаны на использовании электрических и электромагнитных колебаний.

Среди различных колебательных систем особое место занимают электромагнитные системы, при которых электрические величины (токи, заряды) периодически изменяются и которые сопровождаются взаимными превращениями электрического и магнитного полей.

Для возбуждения и поддержания электромагнитных колебаний используется колебательный контур. Колебательный контур — это электрическая цепь, состоящая из последовательно включенных резистора, катушки индуктивности и конденсатора. Именно такой колебательный контур нашел широкое применение в радиоаппаратуре.

Цель данной работы — исследовать механизм электромагнитных колебаний в RLC контуре на примере его компьютерной модели и подтвердить теоретические выводы, используя реальный RLC-контур, на практике.

Для этого необходимо решить следующие задачи:

· исследовать компьютерную модель RLC-контура в программе «Открытая физика», найти резонансную частоту контура, на резонансной частоте исследовать зависимость добротности контура от сопротивления, построить графики.

· исследовать реальный RLC-контур с использованием компьютерной программы «Audiotester», а в качестве генератора частоты — звуковую плату компьютера. Также найти резонансную частоту контура, на резонансной частоте исследовать зависимость добротности контура от сопротивления и построить графики.

· сделать выводы о совпадении теоретических и практических результатов.

Новизна данной работы заключается в том, что в практической части используется компьютер, звуковая плата которого заменяет генератор переменной частоты и вольтметр переменного напряжения. Для управления звуковой платой и обработки информации применяется специальная программа «Audiotester».

1.  Основные положения

Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.

Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой W, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте W₀.

Если частота W₀ свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте W внешнего источника.

Явление возрастания амплитуды колебаний тока при совпадении частоты W внешнего источника с собственной частотой W₀ электрической цепи называется электрическим резонансом. При последовательном резонансе (W = W₀) амплитуды U_C и U_L напряжений на конденсаторе и катушке резко возрастают.

Существует понятие добротности RLC-контура. Она равна отношению амплитуды напряжения на конденсаторе Uc к амплитуде напряжения генератора U: Q = Uc/U.

На рисунке изображен последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рисунок 1):

e(t) = ₀ cos ωt,

где: ₀ — амплитуда,

ω — круговая частота.

 

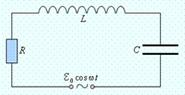
Рисунок 1. Вынужденные колебания в контуре.

 

2.  Исследование компьютерной модели RLC-контура.

Изучим механизм возникновения вынужденных электрических колебаний и вхождения системы в резонанс; определим зависимость тока в контуре от частоты генератора. Для этого будем использовать программу «Открытая физика 1.1» [1, c. 135] .

Запустим на компьютере модель RLC-контура. Появившееся окно эксперимента разбито на несколько частей (рисунок 2). В левой верхней части окна изображена электрическая схема контура. В правой верхней части окна расположена резонансная кривая контура. В левой нижней части находятся движки изменения сопротивления, индуктивности, емкости контура и частоты колебаний генератора. В правой нижней части окна показана векторная диаграмма напряжений и тока в элементах контура. Кнопки вверху слева вызывают звуковое сопровождение, документ с теоретической частью и справочную информацию.

 

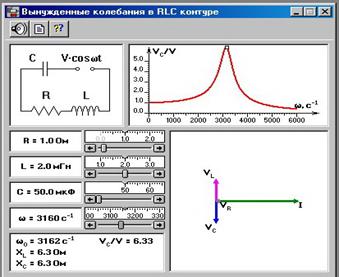
Рисунок 2.

 

В компьютерной модели можно изменять параметры RLC-контура, а также частоту W внешнего источника. При изменении параметров на дисплее высвечивается новая резонансная кривая, на которой точкой отмечается результат компьютерного эксперимента. Одновременно высвечивается векторная диаграмма, на которой с помощью векторов изображаются колебания тока и напряжений на элементах цепи.

Выбираем значения параметров RLC-контура: С=50 мкФ, R=1 Ом, L=2 мГн.

Рассчитаем собственную циклическую частоту Wo , собственную частоту fo контура и добротность Q.

Wo = 1/, fo = Wo/(2*П), Q = Uc/U.

Получаем: Wo = 3162 с-¹, fo= 503,5 Гц , Q = 1,24

В состоянии резонанса будем увеличивать сопротивление R и отслежи-вать значение добротности контура Q на экране. Данные заносим в таблицу 1.

Таблица 1

 

Построим график зависимости добротности контура от активного сопро-тивления в состоянии резонанса (W=Wo):

 

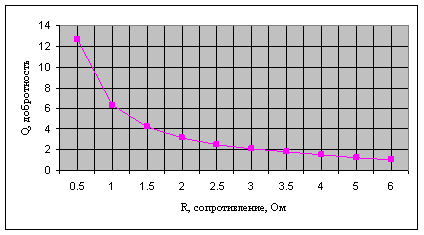
Рисунок 3. График зависимости добротности от активного сопротивления в состоянии резонанса

 

Из графика хорошо видно, что с увеличением сопротивления добротность контура падает.

Рассчитаем в состоянии резонанса реактивные сопротивления Хс и ХL для данной колебательной системы (С=50 мкФ, R=1 Ом, L=2 мГн) Хс = 1/(W*C) , XL = W*L. Получаем: Xc = 6.329 Ом, ХL = 6.32 Ом.

Смотрим на компьютерной модели значения Xc и ХL = 6,3 Ом (рисунок 2). Расчетные значения совпали со значениями модели почти точно.

Теперь изменяем параметры системы: емкость С = 50 мкФ, сопротивление R = 2 Ом, индуктивность L = 2 мГн.

Используя компьютерную модель, рассчитываем полное сопротивление цепи переменного тока, силу тока по формулам:

Z = , I=U/Z и заполняем таблицу 2:

Таблица 2.

 

Строим график зависимости действующего значения тока в контуре от циклической частоты (рисунок 4):

 

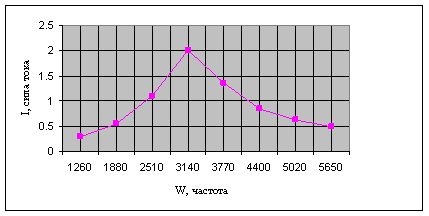
Рисунок 4. График зависимости силы тока от частоты

 

И график зависимости добротности от циклической частоты (рисунок 5):

 

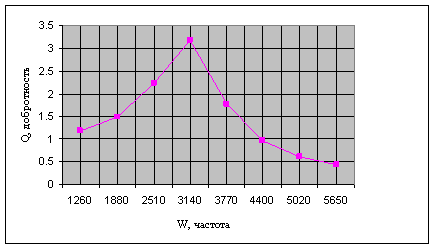
Рисунок 5. График зависимости добротности от частоты

 

Таким образом можно сделать следующие выводы:

· резонанс в цепи с колебательным контуром наступает при совпадении частоты генератора W c частотой колебательного контура Wo;

· с увеличением сопротивления добротность контура падает. Самая высокая добротность при небольших значениях сопротивления контура;

· самая высокая добротность контура ― на резонансной частоте;

· полное сопротивление контура минимально на резонансной частоте.

3. Экспериментальное исследование RLC-контура.

Теперь проведем экспериментальное исследование RLC контура с реальными катушкой индуктивности, конденсатором, сопротивлением и подтвердим совпадение теоретических и экспериментальных измерений. Для исследования RLC контура при различных значениях R будем использовать переменное сопротивление.

Для проведения эксперимента необходим генератор переменного напряжения, вольтметр или амперметр переменного тока и сам RLC контур. В качестве генератора переменного напряжения и вольтметра мы будем использовать компьютер, оснащенный аудиокартой. Существует ряд программ по управлению выходным сигналом аудиокарты и измерению входного сигнала, поступающего на аудиокарту, что и позволяет производить радиотехнические измерения с использованием реальных радиотехнических деталей.

Таким образом состав исследовательской установки включает в себя:

компьютер с аудиокартой, исследуемый RLC контур, комплекс программ AudioTester, вольтметр для калибровки аудиокарты компьютера, тестер для измерения сопротивления контура.

В комплекс компьютерной программы AudioTester входят три программы:

1.программа «Генератор», позволяющая получить на выходе аудиокарты переменные напряжения различной частоты, формы и амплитуды;

2.программа «Осциллограф», позволяющая на экране компьютера наблюдать сигналы, поступающие на вход аудиокарты;

3.и непосредственно сама программа AudioTester, позволяющая производить различные радиотехнические измерения.

Схема установки для исследования изображена на рисунке 6.

 

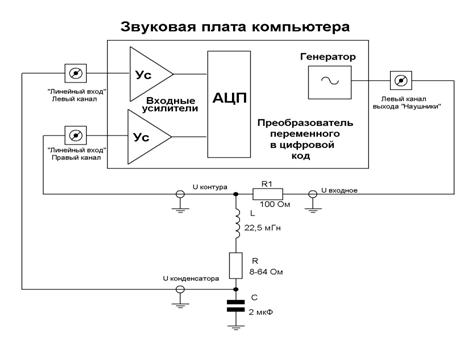
Рисунок 6. Схема измерительной установки

 

В теоретической части измерялся ток, здесь будем измерять напряжения на контуре и отдельно на конденсаторе. Так как сопротивление RLC контура, особенно на частоте резонанса, мало, в схему было добавлено сопротивление R1, ограничивающее ток через схему. Это позволило использовать относительно слабый выход звуковой платы (разъем «наушники») для получения переменного напряжения. Катушка и конденсатор выбраны таким образом, что частота резонанса контура не намного отличается от частоты контура, полученной в теоретической части.На фотографии показана собранная установка, представляющая собой RLC контур, подключенный к компьютеру.

 

 

Подготовка к измерениям и калибровка

Рассмотрим подробнее работу программы AudioTester. Эта программа была создана для проведения различных радиотехнических измерений. Программа позволяет получать на выходе аудиокарты сигналы различной частоты, формы и амплитуды, анализировать входной сигнал, поступающий на вход аудиокарты и сохранять все поступающие данные в файлы на диск компьютера. Между входом и выходом аудиокарты подключается исследуемое устройство. Таким образом, мы можем изменять параметры сигнала, подаваемого на вход исследуемого устройства и анализировать сигналы, поступающие с выхода исследуемого устройства. На рисунке 7 показано основное окно программы.

 

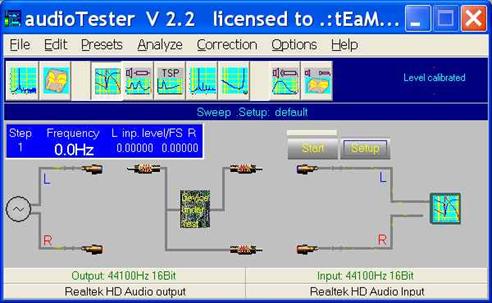
Рисунок 7.

 

В этом режиме программа позволяет генерировать сигнал с изменяемой частотой и измерять два напряжения, поступающие на левый и правый входы аудиокарты. Нажав на кнопку Setup, переходим в окно настроек (рисунок 8):

 

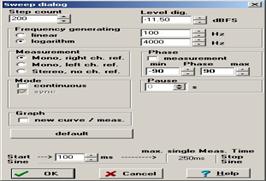
Рисунок 8.

 

Раздел настроек <Frequency generating> позволяет задавать начальную и конечную частоту генератора напряжения.Мы задали диапазон изменения частоты f от 100 до 4000 Гц.

В окне <Step count> задается количество точек, на которое будет разбит заданный частотный диапазон. В данном случае 200.

Для получения достоверных результатов необходимо произвести калибровку выхода аудиокарты (который является генератором) и линейного входа этой же аудиокарты (который используется как вольтметр переменного напряжения).

Калибровка генератора производилась по следующей методике. Задавался частотный диапазон 50—75 Герц, то есть частоты, далекие от частоты резонанса контура и измерялось напряжение на контуре с помощью лампового вольтметра переменного напряжения. Значение в окне <Level dig> подбиралось таким образом, чтобы вольтметр показывал напряжение 0,1 Вольт.

Следующий этап работы ― калибровка линейного входа аудиокарты. Для калибровки входного усилителя аудиокарты использовалось окно Calibration. Здесь выставлялось напряжение <mV rms> в секции <Soundcard input voltage calibration > таким образом, чтобы сигнал на графике зависимости напряжения на контуре от частоты генератора соответствовал 0,1 Вольт, генерируемого аудиокартой (рисунок 9):

 

Рисунок 9.

 

Измерения

Запускаем программу Audiotester. Устанавливаем значение переменного сопротивления R2 = 8 Ом. Измерения напряжения проводились в частотном диапазоне от 100 Герц до 4000 Герц. Как видно из следующего графика, резонансная частота контура равна приблизительно 750 Герц (рисунок 10):

 

Рисунок 10.

 

Получим графики зависимости напряжения на контуре от частоты при различных значениях сопротивления контура R2. Нами измерялось суммарное сопротивление R2 и катушки контура. Это обусловлено тем, что у нас имеется не идеальная катушка, а вполне реальная, имеющая также свое активное сопротивление. Значения R2 устанавливаются равными от 8 до 64 Ом с шагом 8 Ом. Полученные графики представлены на рисунке 11.

 

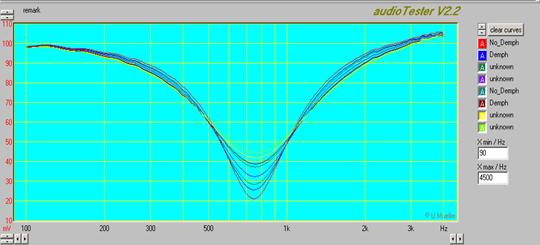
Рисунок 11.

 

Из графиков видно, что напряжение на контуре в точке резонанса существенно зависит от значения R контура. Нижняя кривая соответствует сопротивлению контура, равному 8 Ом, а верхняя ― 64 Ом. Таким образом, видно, что при увеличении значения R напряжение в точке резонанса также увеличивается. На рисунке 12 показаны графики зависимости напряжения на конденсаторе контура от частоты при различных значениях сопротивления R.

Верхняя кривая графика соответствует меньшему значению сопротивления, а нижняя ― большему.

 

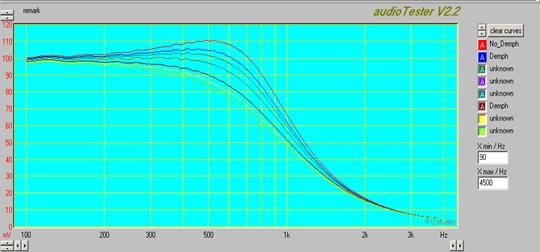
Рисунок 12.

 

Программа AudioTester позволяет сохранить полученные графики в виде табличных файлов. Далее эти данные были перемещены в Excel-таблицу, в которой и были произведены все необходимые вычисления.

Нам известно значение емкости конденсатора C, с помощью программы мы определили резонансную частоту контура fo = 750. Значение индуктивности можно вычислить по следующей формуле:

L = 1 / (2*П * fo) ² * C, L = 1/((2*П*750) ² * 2e^-6) = 0,0225 Гн

Мы получили значение индуктивности 0,0225 Гн.

Затем, изменяя частоту генератора f, измеряем напряжение на контуре (Uк) и напряжение на конденсаторе контура (Uс). Получаем значение добротности для различных частот, которая вычисляется по формуле:

Q = Uс / Uк

Анализируя полученные результаты, можно сделать следующие выводы:

·добротность контура растет с увеличением частоты и достигает максимума на частоте резонанса. При дальнейшем увеличении частоты добротность уменьшается;

·значения добротности на краях заданного частотного диапазона практически не изменяются при изменении сопротивления контура;

·при исследовании изменения добротности на резонансной частоте видно, что значение добротности Q тем выше, чем меньше сопротивление контура R.

Выбрав из полученных результатов значение добротности на резонансной частоте контура для разных значений сопротивления, мы получаем следующую таблицу:

Таблица 3.

 

И график, соответствующий этой таблице:

 

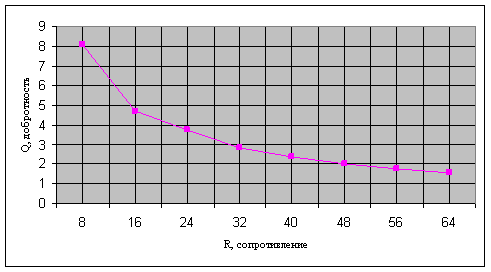
Рисунок 13. График зависимости добротности от сопротивления контура в состоянии резонанса.

 

Также была составлена таблица с результатами вычислений полного сопротивления контура, реактивных сопротивлений катушки индуктивности и конденсатора для различных значений частоты генератора. Активное сопротивление выбрано 8 Ом, С контура ― 2.0 мкФ,

ХL=2*П*f*L ,

Хс=1/(2*П*f*C),

Z=

Приведем часть таблицы

Таблица 4.

 

Выделенные значения соответствуют частоте резонанса контура. Видно, что на низких частотах емкостное сопротивление конденсатора Хс переменному току велико. При увеличении частоты емкостное сопротивление конденсатора Хс убывает. Индуктивное сопротивление ХL катушки мало на низких частотах, но увеличивается с ростом частоты.

На резонансной частоте индуктивное сопротивление ХL катушки равно емкостному сопротивлению конденсатора Хс. Полное сопротивление на частоте резонанса имеет минимальное значение (рисунок 14):

 

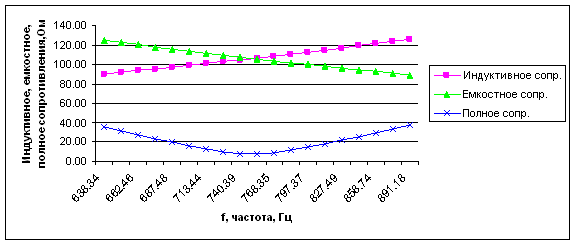
Рисунок 14. График зависимости индуктивного, ёмкостного и полного сопротивления от частоты генератора.

 

Полученные нами выводы в практической части работы полностью согласуются с выводами, сделанными нами в теоретической части при изучении компьютерной модели RLC-контура.

Заключение

Таким образом в данной работе проведены теоретические и практические исследования работы RLC-контура в цепи переменного тока.

Мы исследовали компьютерную модель RLC-контура в программе «Открытая физика», нашли резонансную частоту контура, на резонансной частоте исследовали зависимость добротности контура от сопротивления и построили графики.

В практической части работы исследовали реальный RLC-контур с использованием компьютерной программы «Audiotester». Нашли резонансную частоту контура, на резонансной частоте исследовали зависимость добротности контура от сопротивления и построили графики.

Выводы, сделанные нами в теоретической и практической части работы, совпали полностью.

Применение в практической части специальной программы «Audiotester» позволило провести исследования в широком диапазоне значений частоты без дополнительных измерительных приборов, получить и сохранить данные на компьютере, произвести их компьютерную обработку и построить графики на экране компьютера разных величинных зависимостей.

 

Список литературы:

1.Сорокин А.В., Торгашина Н.Г., Ходос Е.А., Чиганов А.С. Физика: наблюдение, эксперимент, моделирование. Элективный курс: Методическое пособие. М.: БИНОМ. Лаборатория знаний, 2006. ― 175 c.