СРАВНЕНИЕ  МОДЕЛЕЙ  НЕЙРОННОЙ  СЕТИ  ДЛЯ  ПРОГНОЗИРОВАНИЯ  ВРЕМЕННЫХ  РЯДОВ

Хужаев  Отабек  Кадамбаевич

ассистент  преподаватель,  кафедра  «Информационный  технологии»,  Ургенчский  филиал  Ташкентского  университета  информационных  технологий,  Республика  Узбекистан,  г.  Ургенч

E-mail: 

Ядгаров  Шерзод  Абдуллаевич

ассистент  преподаватель,  кафедра  «Информационный  технологии»,  Нукусский  филиал  Ташкентского  университета  информационных  технологий,  Республика  Узбекистан,  г.  Нукус

E-mail: 

Пак  Виталий  Станиславович

ассистент  преподаватель,  кафедра  «Информационный  технологии»,  Ташкентского  университета  информационных  технологий,  Республика  Узбекистан,  г.  Ташкент

E-mail:  

COMPARISON  OF  NEURAL  NETWORKS  MODELS  FOR  TIME  SERIES  PREDICTION

Khujaev  Otaber

assistant  prof.,  “Information  technology”  department  Urganch  branch  of  Tashkent  University  of  information  technologies,  Uzbekistan,  Urganch

Yadgarov  Sherzod

assistant  prof.,  “Information  technology”  department  Nukus  branch  of  Tashkent  University  of  information  technologies,  Uzbekistan,  Nukus

Pak  Vitaliy

assistant  prof.,  “Information  technology”  department

Tashkent  University  of  information  technologies,  Uzbekistan,  Tashkent

АННОТАЦИЯ

В  работе  описывается  использование  двух  моделей  нейронных  сетей  для  решения  проблемы  прогнозирования  временных  рядов.  Скользящее  окно  использовалось  вместе  с  исходным  (начальным)  методом  обработки  данных.  В  статье  рассматривается  сравнение  возможностей  прогнозирования  моделей  Эльмана  и  прямо  распространённых  нейронных  сетей.  Результаты  были  получены  с  использованием  библиотеки  Neural  Network  Toolbox  IDE  MatLab.

ABSTRACT

This  article  describes  the  use  of  two  models  of  neural  networks  for  solving  the  problem  of  time  series  prediction.  With  initial  data  processing  method  was  used  a  sliding  window.  The  article  focuses  on  comparing  prediction  capabilities  of  the  models  Elman  and  feedforward  neural  networks.  The  results  were  obtained  using  the  library  neural  network  toolbox  IDE  MatLab. 

Ключевые  слова :  Рекуррентная  нейронная  сеть  Эльмана;  нейронная  сеть  прямого  распространенная;  скользящее  окно;  обратное  распространение;  NIO;  NARX. 

Keywords :  Elman  recurrent  neural  networks;  feedforward  neural  networks;  sliding  window;  backpropagation;  NIO;  NARX.

1.Введение 

В  последние  годы,  в  прогнозировании  широко  используются  методы  искусственного  интеллекта,  такие,  как  экспертные  системы,  искусственные  нейронные  сети  и  т.  д.  Существует  много  моделей  нейронных  сетей.  В  прогнозировании  чаще  всего  используются  методы  нейронной  сети  прямого  распространения  и  нейронные  сети  Элмана  с  обратными  связями,  в  которых  применяется  скользящее  окно  над  входной  последовательностью  [5]  [11].  Целью  данной  работы  является  сравнение  строения  нейронных  сетей  Эльмана  и  нейронной  сети  прямого  распространения  для  прогнозирования  временных  рядов.

1.1.   Прогнозирования  временных  рядов  и  раздвижные  окна

Временной  ряд  представляет  собой  последовательность  векторов,  x(t),  t=0,1,…..,  где  t  —  истекшее  время.  С  целью  упрощения  мы  будем  рассматривать  здесь  только  последовательности  скаляров,  хотя  рассматриваемые  методы  легко  обобщить  вектору  серии.  Теоретически  х  может  быть  значением,  которое  изменяется  непрерывно  с  t  таких,  как  температура,  но  на  практике,  для  любой  заданной  физической  системы,  х  будет  выбран,  так,  чтобы  дать  серию  дискретных  точек  данных,  равномерно  распределенных  во  времени.  Например,  временных  рядов  по  часам,  по  дням,  по  неделям,  по  месяцам.  Метод  скользящего  окна  помогает  нам  создавать  учебный  набор  данных,  например:  х(1),  х(2),  х(3)  ......  х(n)  является  вектором  временных  рядов.  После  использования  скользящего  окна,  размер  которого  равен  d,  мы  можем  создать  это  отображение  набора  данных  ввода-вывода.

1.2.  Нейронная  сеть  прямого  распространения  и  нейронная  сеть  Эльмана

Нейронная  сеть  прямого  распространения  содержит  входной  слой,  скрытые  слои,  выходной  слой.  В  нейронной  сети  прямого  распространения  все  нейроны  и  входные  блоки  соединены  с  передним  нейроном  и  не  связаны  с  нейронами,  которые,  расположены  в  том  же  слое  и  в  предыдущем  [10].  Сети  Эльмана  —  периодически  повторяющиеся  сети,  которые  были  предложены  Эльманом  в  1990  г.  [6].  Они  похожи  на  сети  прямого  распространения,  но  они  имеют  обратную  связь  в  спрятанных  слоях.  Схемы  нейронных  сетей  прямого  распространения  и  сетей  Эльмана  представлены  на  рисунке  1,  который  используется  для  прогнозирования  [5].

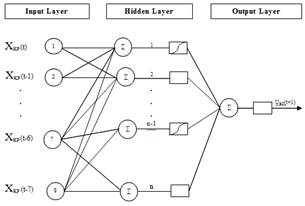
Рисунок  1.  Строение  нейронных  сетей  прямого  распространения  и  сетей  Эльмана

Теоретически  там  будет  много  скрытых  слоев,  но  практически  обычно  используется  один  скрытый  слой  [7]  [8].  Количество  единиц  входного  слоя  будет  равно  размеру  окна.  Мы  не  можем  сказать,  сколько  нейронов  мы  вкладываем  в  скрытый  слой,  потому  что,  чем  больше  скрытых  нейронов,  тем  больше  вычислений.  Поэтому  оптимальное  количество  скрытых  нейронов  будет  отличаться  для  каждого  набора  данных. 

В  качестве  функции  активации  обычно  используется  простая  дифференцируемая  нелинейная  логистическая  функция.

                                                         (1)

Если  мы  прогнозируем  переменную,  которая  может  принимать  отрицательные  значения,  то  лучше  использовать  гиперболический  тангенс  как  функцию  активации:

                                                       (2)

2.  Обучение  и  тестирование  нейронной  сети 

В  обучении  мы  используем  метод  обратного  распространения.  Метод  обратного  распространения  является  одним  из  простейших  и  наиболее  общих  методов  контролируемого  обучения  многослойных  нейронных  сетей  [9].  Основной  подход  в  обучении  —  это  начать  с  неподготовленной  сети,  представить  учебный  образец  во  внутреннем  слое,  передать  сигналы  через  сеть  и  определить  выход  в  выходном  слое.  Здесь  эти  выходы  сравниваются  с  целевыми  значениями;  любое  отличие  соответствует  ошибке.  Эта  ошибка  или  критерий  функции  —  это  некоторая  скалярная  функция  весов  и  сводится  к  минимуму,  когда  сетевые  выходы  соответствуют  желаемым  результатам.

Мы  рассматриваем  ошибку  обучения  в  образце  как  сумму  входных  единиц  квадрата  разности  между  желаемым  выходным  t_k,  значением,  заданным  учителем,  и  фактической  выходной  z_k,  также  как  мы  имели  в  алгоритме  наименьшего  среднеквадратичного  (LMS)  для  двухслойной  сети.

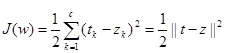                      (3)

Здесь  t  и  z  —  целевой  и  сетевой  выходной  векторы  с  длинами  с  и  w,  представляющие  все  веса  в  сети. 

Правило  обучения  обратного  распространения  основывается  на  градиентном  спуске.  Веса  инициализируются  случайными  значениями,  а  затем  они  меняются  в  направлении,  которое  позволит  снизить  ошибку:

,                                           (4)

где    —  скорость  обучения,  и  лишь  указывает  на  относительную  величину  изменений  в  весах.  Уравнение  4  довольно  простое:  они  просто  требуют,  чтобы  мы  сделать  шаг  в  весовом  пространстве,  что  снижает  функцию  критерия.  Как  видно  из  уравнения  3,  целевая  функция  может  быть  отрицательной;  более  того,  скорость  обучения  гарантирует,  что  обучение  остановится,  за  исключением  патологических  случаев.  Этот  повторяющийся  алгоритм  требует  принятия  весового  вектора  на  итерации  m  и  обновление  его  как

.                        (5)

Где  m  индексирует  частную  модель  представления.

Завершение  обучающего  алгоритма  оптимизирует  синоптические  взвешенные  соединения  установить  надежные  отношения  между  входами  и  выходами.  Во  время  этапа  тестирования  и  проверки  эти  свободные  параметры  остаются  неизменными,  в  то  время  как  новые  входы  подаются  в  сети,  чтобы  произвести  серию  выходов.  Эти  выходы  сравниваются  с  набором  тестовых  данных,  соответствующих  фактически  полученным  результатам.  Если  фактический  выход  отличается  от  заданного  набора  тестовых  выходов  больше  порогового  значения  ошибки,  то  необходимо  скорректировать  обучение  и  заново  подготовить  нейронную  сеть.

3.  Эксперименты

Для  эксперимента,  у  нас  есть  набор  данных  временных  рядов,  который  дает  почасовую  информацию  о  высоте  воды  реки  Лагун  из  Венеции.  Этот  набор  данных  содержит  информацию  о  высоте  воды  в  1990—1995  годы  по  часам.  Мы  используем  85  %  данных  для  обучения  сети  и  15  %  данных  для  тестирования.  В  учебном  процессе  мы  используем  алгоритм  метода  обратного  распространения  Levenberg-Marquart.  Результаты  были  получены  с  помощью  библиотеки  Neural  Network  Toolbox  IDE  MatLab.  В  MatLab  есть  специальные  сети  для  прогнозирования  временных  рядов.  К  ним  относятся:  NARX  (Нелинейная  авторегрессия  с  внешним  источником)  сеть  основанная  на  нейронной  сети  Эльмана,  сеть  NIO  (Нелинейная  ввода-вывода)  на  основе  нейронной  сети  прямого  распространения.

3.1.  Прогнозирование  результатов  с  сетью  NARX.

Рисунок.  2.  Структура  сети  NARX

Рисунок  3.  Средняя  квадратичная  ошибка

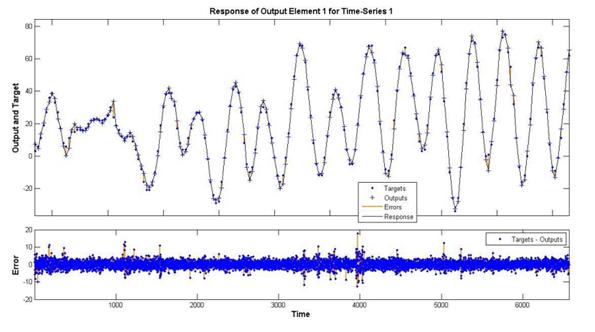
Рисунок  4.  Результат  тестирования

3.2.             Прогнозирование  результатов  с  NIO  сети.

Рисунок  5.  Структура  сети  NIO

Рисунок  6.  Средняя  квадратичная  ошибка

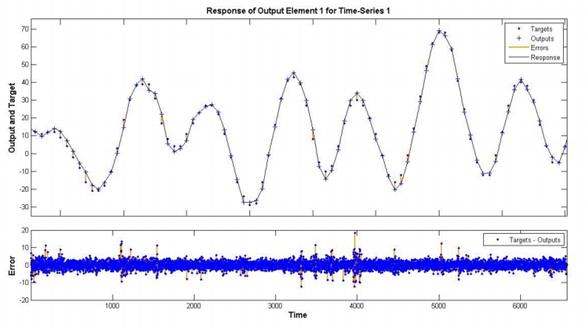
Рисунок  7.  Результат  тестирования

4.  Заключение

Наше  исследование  показало,  что  нейронные  сети  прямого  распространения  и  нейронные  сети  Эльмана  хорошо  применимы  для  прогнозирования  временных  рядов.  Для  обучения  мы  использовали  алгоритм  обратного  распространения  для  нейронных  сетей  Levenberg-Marquart.  Наши  эксперименты  показывают,  что  модель  нейронной  сети  NARX  более  эффективна,  чем  модель  нейронной  сети  NIO  и,  что  процесс  обучения  также  не  занимает  больше  времени  в  модели  нейронной  сети  NARX,  чем  в  модели  нейронной  сети  NIO.  В  нашем  эксперименте  наборов  данных  мы  используем  только  последние  15  %  данных  в  тестировании.  Такой  подход  помогает  нам  выбрать  наилучшую  структуру  сети  для  задач  прогнозирования.

Список  литературы:

1.Царегородцев  В.Г.,  Взгляд  на  архитектуру  и  требования  к  нейроиммитатору  для  решения  современных  индустриальных  задач,  Всероссийский  семинар  «Нейроинформатика  и  ее  приложения»,  Красноярск  2003.

2.Царегородцев  В.Г.  Оптимизация  предобработки  данных  для  обучаемой  нейросети:  критерии  оптимальности  предобработки,  Международная  конференция  по  нейрокибернетике,  Растов-н/Д.,  2005.

3.Christopher  M.  Bishop.  Pattern  Recognition  and  Machine  Learning.  Springer  Science  +Business  Media,  LLC  2006  y.

4.Hanh  H.  Nguyen,  Christine  W.  Chan.  Multiple  neural  networks  for  a  long  term  time  series  forecast.  Neural  Comput  and  Applic  (2004)  13:  90—98.

5.Jeffery  D.  Martin,  Yu  T.  Morton,  Qihou  Zhou.  Neural  network  development  for  the  forecasting  of  upper  atmosphere  parameter  distributions.  Advances  in  Space  Research  36  (2005)  2480—2485  p.  Expert  Systems  with  Applications  39(2012)  4344—4357.

6.Liang  Yongchun.  Application  of  Elman  Neural  Network  in  Short-Term  Load  Forecasting.  International  Conference  on  Artificial  Intelligence  and  Computationl  Intelligence  2010  y.

7.Mehdi  Khashei,  Mehdi  Bijari.  A  new  class  of  hybrid  models  for  time  series  forecasting.  Expert  Systems  with  Applications  39(2012)  4344—4357.

8.Mehdi  Khashei,  Mehdi  Bijari.  An  artificial  neural  network  (p.d.q)  model  for  timeseries  forecasting.  Expert  Systems  and  Applications  37(2010)  479—499  p.

9.Richard  O.  Duda,  Peter  E.  Hart,  David  G.  Stock  Pattern  Classification.  John  Wiley  &  Sons  2001  y.

10.Sven  F.  Crone,  Stefan  Lessmann  and  Swantje  Pietsch.  Forecasting  with  Computational  Intelligence-  an  Evaluation  of  Support  Vector  Regrassion  and  Artificial  Neural  Networks  for  Time  Series  Prediction.  International  Joint  Conference  on  Neural  Networks,  2006  y.

11.Zaiyong  Tang,  Paul  A.Fishwick.  Feed-forward  Neural  Nets  as  Models  for  Time  Series  Forescasting.  Department  of  Computer  &  Information  Sciences,  University  of  Florida