МОДЕЛИРОВАНИЕ  НАГРЕВА  ПЛАСТИНЫ  РЕЗЦА

Омельченко  Светлана  Владимировна

канд.  пед.  наук,  Южно-Уральский  государственный  университет,  РФ,  г.  Челябинск

E-mail: 

MODELING  OF  THE  HEATING  OF  A  HALF-LOG  BLADE

Svetlana  Omelchenko

candidate  of  Pedagogic  Sciences,  South  Ural  State  University,  Russia,  Chelyabinsk

АННОТАЦИЯ

Статья  посвящена  вопросам  математического  моделирования  процесса  нагрева  пластины  отрезного  резца  в  двумерном  случае  с  учетом  теплоотдачи.

ABSTRACT

The  article  is  devoted  to  questions  of  math  modeling  of  the  heating  process  of  a  half-log  cutoff  blade  in  a  two-dimensional  case  with  account  for  heat  dissipation.

Ключевые  слова:   моделирование;  теплопроводность;  нагрев.

Keywords:  modeling;  heat  conduction;  heating.

Механическая  обработка  сопровождается  значительным  выделением  тепла  в  элементах  технологической  системы.  Большие  тепловые  воздействия  испытывает  инструмент  при  резании  жаропрочных,  коррозионностойких,  тугоплавких  металлов  и  их  сплавов,  а  так  же  при  резании  материалов  без  применения  СОЖ  [1;  5].

Высокие  температуры  нагрева  контактных  поверхностей  инструмента  повышают  интенсивность  его  изнашивания  и  снижают  период  заданной  стойкости.  Вследствие  этого  анализ  теплового  состояния  инструмента  является  одним  из  важнейших  условий  научно  обоснованного  проектирования  технологического  процесса  механической  обработки,  выбора  инструмента  и  назначения  режимов  резания  [5;  6].

В  настоящее  время  широко  используются  экспериментальные  и  аналитические  методы  определения  температуры  рабочей  части  резцов  [1;  2].  Недостатком  экспериментальных  способов  определения  температур  является  сложность  технических  средств  и  значительные  затраты  на  проведение  эксперимента.  В  ряде  случаев  вообще  не  удаётся  измерить  температуру  в  нужной  части  лезвия  [1;  5].

Существующие  расчётные  методики  для  определения  температурных  полей  в  ограниченных  пластинах  при  стационарном  и  нестационарном  режимах  часто  основаны  на  моделях  точечных  и  линейных  источников  тепла  [4;  7].  Такое  упрощение  не  позволяет  найти  температуру  непосредственно  в  зоне  действия  источника.  Кроме  того,  во  многих  известных  исследованиях  температура  определяется  при  стационарном  режиме  без  учёта  теплообмена  с  окружающей  средой.

В  данной  работе  предлагается  построение  математической  модели  проходного  резца  (рисунок  1),  которая  учитывает  нестационарность  процесса,  конечные  размеры  источника  тепла,  теплообмен  с  окружающей  средой,  форму  и  геометрию  инструмента.

В  работе  [2]  построена  трехмерная  модель  отрезного  резца,  имеющая  сложный  вид  и  не  приведенная  к  инженерному  виду.  Для  упрощения  модели  в  настоящей  работе  предлагается  исключить  влияние  ширины  резца  на  распределение  температурных  полей.  Фактически  предполагается,  что  резание  происходит  всей  режущей  кромкой  резца,  что  на  практике  наблюдается  в  подавляющем  большинстве  случаев.

Дифференциальное  уравнение  теплопроводности  для  двумерной  модели  резца  представляется  в  следующем  виде  [3]:

,

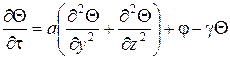где:    —  приращение  температуры; 

,    —  координаты; 

  —  время; 

  —  коэффициент  температуропроводности  материала  резца; 

  —  функция  источников  тепла; 

q  —  плотность  тепловыделения  указанных  источников; 

c,    —  теплоемкость  и  плотность  материала  инструмента; 

  —  приведенный  коэффициент  теплоотдачи;  .

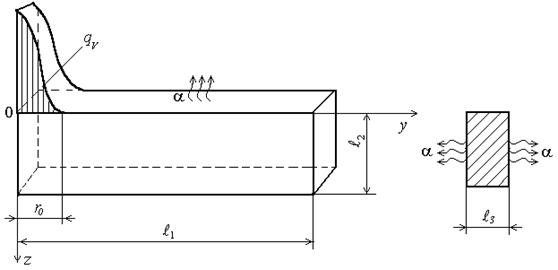
Рисунок  1.  Модель  отрезного  резца

Внутренние  источники  тепла  должны  соответствовать  мощности  и  форме  подвода  тепла  к  резцу  из  зоны  резания.  Из  этих  соображений  функции    целесообразно  придать  вид 

.

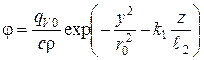Начальное  и  граничные  условия  задаются  соотношениями  [2;  6;  7]: 

;

;  ;

;  .

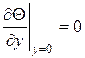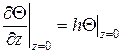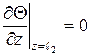Первое  равенство  означает,  что  теплообмен  задней  поверхности  резца  с  незначителен.  Второе  равенство  объясняется  интенсивным  охлаждением  нерабочей  части  инструмента  в  резцедержателе  [5].

Решение  уравнения  теплопроводности  при  заданных  условиях  дает  выражение  для  расчета  нестационарных  температурных  полей:

.

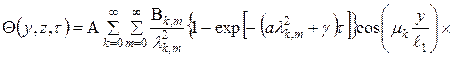
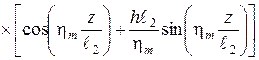Здесь

;

;

;  .

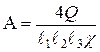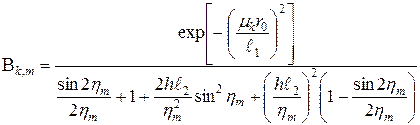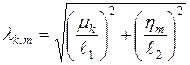Тепловой  поток  ,  связанный  с  плотностью  тепловыделения    зависимостью  ,  часто  находится  экспериментальным  путем  [1;  2].

Корни    определяются  из  уравнения,  вытекающего  из  граничного  условия  .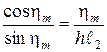

Расчет  температурного  поля  резца  можно  производить  для  различных  моментов  времени    и  различных  величин  теплоотдачи  .  При  этом  в  качестве  базовых  можно  использовать  следующие  исходные  данные:  материал  резца  —  Р18;    =  20  Вт;    =  0,05  м;    =  0,03  м;    =  0,005  м;    =  0,0005  м;    =  400  Дж/(кг×°С);    =  8000  кг/м³;    =  32  Вт/(м×°С);    =  10^-5  м²/с;    =  1  с;    =  10  с;    =  100  с;    =  10  Вт/(м²×°С).

Список  литературы:

1.Макаров  А.Д.  Оптимизация  процессов  резания  /  А.Д.  Макаров.  М.:  Машиностроение,  1976.  —  278  с. 

2.Пашацкий  Н.В.  Нагрев  лезвия  проходного  резца  /  Н.В.  Пашацкий,  А.В.  Прохоров  В.В.  Закураев,  А.А.  Шивырев  //  СТИН.  —  2003.  —  №  4.  —  С.  21—23.

3.Пашацкий  Н.В.  Тепловые  процессы  при  обработке  предварительно  нагретой  стальной  плиты  огневой  машиной  /  Н.В.  Пашацкий,  А.В.  Прохоров  //  Известия  ВУЗов.  Черная  металлургия.  —  2001.  —  №  3.  —  С.  46—48.

4.Прохоров  А.В.  Моделирование  движущихся  приповерхностных  источников  тепла  /  А.В.  Прохоров  //  Инновации  в  науке.  —  2013.  —  №  16-1.  —  С.  16—20.

5.Старков  В.К.  Обработка  резанием.  Управление  стабильностью  и  качеством  в  автоматизированном  производстве  /  В.К.  Старков.  М.:  Машиностроение,  1989.  —  296  с.

6.Талантов  Н.В.  Физические  основы  процесса  резания,  изнашивания  и  разрушения  режущего  инструмента  /  Н.В.  Талантов.  М.:  Машиностроение,  1992.  —  240  с.

7.Osovets  S.V.  Calculation  of  the  Unsteady  Thermal  State  of  a  Slab  Heated  by  a  Moving  Source  /  S.V.  Osovets,  E.V.  Toropov,  A.V.  Prokhorov,  V.L.  Kirillov  //  Journal  of  Engineering  Physics  and  Thermophysics.  —  2000.  —  V.  73,  —  №  4.  —  P.  745—748.