ОПТИМАЛЬНАЯ  ПРОГРАММА  УПРАВЛЕНИЯ  В  ЗАДАЧЕ  ФОРМИРОВАНИЯ  ВЫСОТЫ  ПЕРИГЕЯ  С  ИСПОЛЬЗОВАНИЕМ  МАЛОЙ  ТЯГИ

Ишков  Сергей  Алексеевич

д-р  техн.  наук,  профессор  Самарского  государственного  аэрокосмического  университета  (национального  исследовательского  университета),  РФ,  г.  Самара

E -mail:  ishkov@ssau.ru

Филиппов  Григорий  Александрович

специалист,  инженер  Самарского  государственного  аэрокосмического  университета  (национального  исследовательского  университета),  РФ,  г.  Самара

E-mail: 

OPTIMAL  CONTROL  IN  PROBLEM  OF  FORMING  OF  HEIGHT  OF  PERIGEE  WITH  LOW  –  TRUST

Ishkov  Sergey

doctor  of  technical  science,  Associate  professor  of  Samara  State  Aerospace  University  (National  Research  University),  Russia,  Samara

Filippov  Grigoriy

specialist,  Engineer  of  Samara  State  Aerospace  University  (National  Research  University),  Russia,  Samara

АННОТАЦИЯ

Рассматривается  задача  управления  высотой  перигея  высокоэллиптической  орбиты.  Получена  локально-оптимальная  программа  управления  ориентацией  вектора  тяги  на  витке.  С  использованием  принципа  максимума  Л.С.  Понтрягина  сформулирована  и  решена  краевая  задача  оптимального  управления  перигеем  орбиты.  Приведён  сравнительный  анализ  программ  управления  для  задачи  утилизации  космического  мусора.

ABSTRACT

The  problem  of  control  of  perigee  of  high  elliptical  orbit  is  studied.  The  locally-optimum  program  of  control  of  orientation  of  the  trust  vector  of  the  propulsion  system  is  obtained.  Using  Pontryagin  maximum  principle,  the  boundary  value  problem  of  optimal  control  of  perigee  is  formulated  and  solved.  The  comparative  analysis  of  the  resultsis  shown.

Ключевые  слова:   высота  перигея;  оскулирующие  элементы;  локально-оптимальная  программа  управления  ориентацией  вектора  тяги;  принцип  максимума  Понтрягина;  краевая  задача.

Keywords:  the  height  of  perigee;  osculating  elements;  locally-optimum  trust  vector  control  program;  Pontryagin  maximum  principle;  boundary  value  problem.

Радиус  перигея  орбиты,  как  известно,  определяет  минимальное  расстояние  от  космического  аппарата  до  поверхности  Земли  и  является  важной  характеристикой,  определяемой  срок  существования  космического  аппарата  на  орбите.

В  данной  работе  рассматривается  задача  оптимального  и  локально-оптимального  управления  радиусом  перигея  орбиты  с  использованием  на  борту  космического  аппарата  двигателя  малой  тяги.

Данная  задача  является  актуальной  при  реализации  операции  увода  и  спуска  с  орбиты  космического  мусора.  Применение  для  этих  целей  специального  многоразового  космического  аппарата  —  сборщика  мусора,  снабжённого  электрореактивными  двигателями  малой  тяги  позволяет  повысить  эффективность  процедуры  утилизации  космического  мусора  [1].

Введём  в  рассмотрение  систему  дифференциальных  уравнений  в  оскулирующих  элементах,  описывающих  движение  космического  аппарата  в  плоскости  орбиты  [2]:

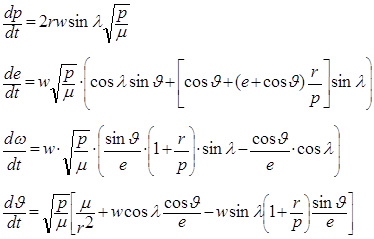            (1)

где:  р  —  фокальный  параметр  орбиты, 

e   —  эксцентриситет  орбиты,

  —  аргумент  перигея, 

r   —  геоцентрическое  расстояние  ,

—  истинная  аномалия, 

—  гравитационный  параметр  Земли, 

—  угол  между  вектором  тяги  реактивной  струи  и  радиус  вектором  в  плоскости  орботы, 

w   —  ускорения  тяги.

Так  как  двигатель  работает  без  выключений  и  является  нерегулируемым,  то  единственным  параметром  управления  будет  угол  .

В  качестве  допущения  примем,  что  реактивное  ускорение  мало  по  сравнению  с  гравитационным  и  .  На  этом  основании  осуществим  переход  к  новой  независимой  переменной  –  эксцентрической  аномалии  E,  пренебрегая  членами  содержащими  множитель  .  Получим  систему  уравнений  вида:

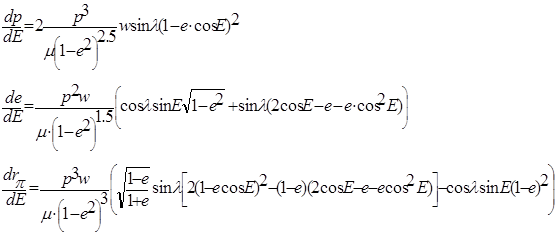    (2)

Поскольку  положение  перигея,  определяемое  ,  не  рассматривается,  то  уравнение  для  него  опущено.

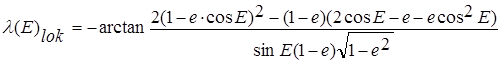Определим  локально  оптимальное  управление  углом  ориентации  вектора  тяги  ,  обеспечивающим  наибольшую  скорость  изменения  радиуса  перигея  .  Для  этого  найдём  решение  уравнения  относительно  управления    [3].

     (3)

Рассмотрим  вопрос  о  предельных  возможностях  управления.  Для  тех  же  допущений  определим  оптимальную  программу  управления  углом  ориентации  тяги    с  использованием  принципа  максимума  Л.С.  Понтрягина  [4].

В  соответствии  с  общим  алгоритмом  принципа  максимума  запишем  гамильтониан  системы  для  критерия 

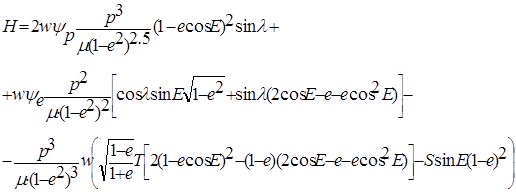  (4)

где  и  —  спряжённые  множители  для  фокального  параметра  и  эксцентриситета  соответственно.

Оптимальное  управление  определится  из  условия  максимума  Н.

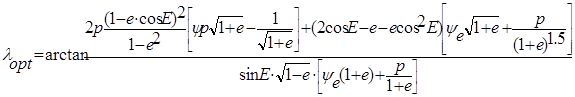         (5)

Уравнения  для  сопряженных  множителей  примут  вид:

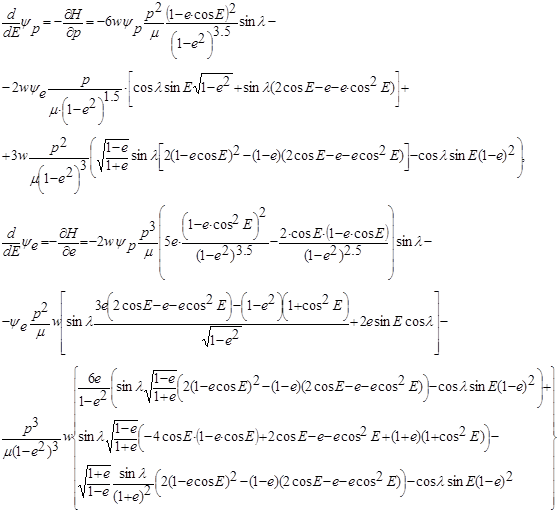    (6)

Из  условий  трансверсальности  в  конечной  точке  ,  значения  сопряженных  множителей  должны  быть  равны  нулю.  Тогда  граничные  условия  решаемой  системы  (2),  (6)  с  учётом  управления  (5)  примут  вид:

                                (7)

Краевая  задача  сводится  к  определению  начальных  значений  сопряжённых  множителей    для  удовлетворения  граничных  условий  (7).  Для  определения  начального  приближения  могут  быть  использованы  решения,  полученные  при  интегрировании  локально-оптимальной  программой  (3).  Краевая  задача  обладает  хорошей  сходимостью  при  интегрировании  из  конечной  точки  в  начальную  с  отрицательным  шагом.

На  рисунке  1  показана  полученная  локально-оптимальная  и  оптимальная  программа  управления  ориентацией  вектора  тяги  на  одном  витке.

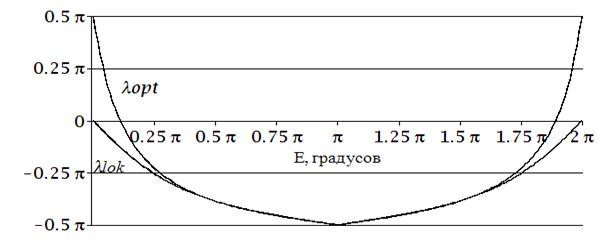
Рисунок  1  Оптимальная  и  локально-оптимальная  программы  управления  ориентацией  вектора  тяги  на  витке

Программы  близки  друг  к  другу  на  всём  диапазоне  значений  углов  эксцентрической  аномалии  ,  за  исключением  точек  в  окрестности  точки 

Проведённые  расчёты  показали,  что  выигрыш  при  использовании  оптимальной  программы  (5)  по  сравнению  с  локально-оптимальной  программой  (3)  составляет  величину  менее  1  %  на  одновитковом  интервале,  на  многовитковом  интервале  5-7  %  в  зависимости  от  граничных  условий  перелета.

Рассмотрим  задачу  формирования  предспусковой  эллиптической  орбиты  с  высотой  перигея  200  км,  используемой  для  реализации  управляемого  спуска  с  орбиты  космического  мусора  с  использованием  малой  тяги.

Варьировалась  высота  перигея    и  высота  апогея    начальной  орбиты  и  рассчитывались  затраты  характеристической  скорости  обеспечивающие  перелёт  по  программе  (3)  с  начальной  орбиты  на  предспусковую. 

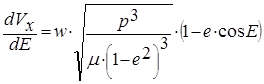                        (8)

Результаты  некоторых  расчётов  представлены  на  рисунке  2  в  виде  линий  уровня  равных  затрат  .  Расчёт  выполнен  для  ускорения  тяги 

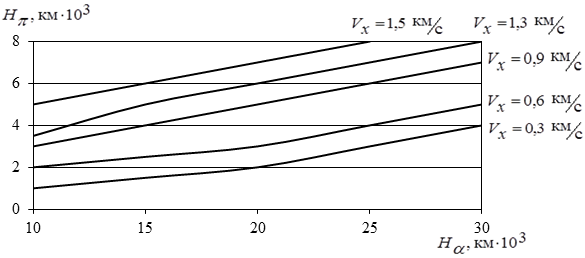
Рисунок  2.  Затраты  характеристической  скорости  для  перевода  КА  с  произвольной  орбиты  на  предспусковую

В  рассматриваемом  диапазоне  параметров  линии  уровня  оказались  близкими  к  линейным  функциям.

Полученные  в  статье  результаты  позволяют  дать  оценку  эффективности  применения  оптимальной  и  локально-оптимальной  программ  управления  высотой  перигея  для  задачи  коррекции  и  вывода  на  предспусковую  орбиту  фрагментов  космического  мусора.

Список  литературы:

1.Ишков  С.А.,  Филиппов  Г.А.  Выбор  проектных  параметров  космического  аппарата  сборщика  —  мусора  с  использованием  малой  тяги  //  Вестник  СГАУ  —  2014.  —  №  3.  —  С.  25—35.

2.Лебедев  В.Н.  Расчет  движения  космического  аппарата  с  малой  тягой.  М.:  ВЦ  АН  СССР,  1968.  —  108  с.

3.Охоцимский  Д.Е.,  Сихарулидзе  Ю.Г.  Основы  механики  космического  полёта.  М.:  Наука.  1990.  —  448  с.

4.Понтрягин  Л.С.,  Болтянский  В.Г.  и  др.  Математическая  теория  оптимальных  процессов  /  под  ред.  Понтрягина  Л.С./  М.:  Наука,  1976,  —  392  с.