Статья опубликована в рамках: XXXIV Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 28 мая 2014 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ОЦЕНКА ВЛИЯНИЯ ВЕРОЯТНОСТНО-ВРЕМЕННЫХ ХАРАКТЕРИСТИК ПРОЦЕССА УПРАВЛЕНИЯ НА ОТКАЗОУСТОЙЧИВОСТЬ МУЛЬТИСЕРВИСНОЙ СЕТИ СВЯЗИ
Дроздов Игорь Александрович
канд. техн. наук, доцент, Академия ФСО России, РФ, г. Орёл
E -mail: 19digor63@mail.ru
Константинов Сергей Владимирович
учитель Академия ФСО России, РФ, г. Орёл
E-mail:
ESTIMATION OF INFLUENCE OF IS PROBABILITY-TIME CHARACTERISTICS OF MANAGERIAL PROCESS ON FAIL SAFETY OF THE MULTISERVICE COMMUNICATION NETWORK
Igor Drozdov
candidate of Technical Science, Associate Professor, Academy of FSGS of the Russian Federation, Russia, Orel
Sergey Konstantinov
teacher, Academy of FSGS of the Russian Federation, Russia, Orel
АННОТАЦИЯ
В статье рассматриваются вопросы, касающиеся механизмов оценки влияния вероятностно-временных характеристик процесса управления на отказоустойчивость мультисервисной сети связи. Предлагаются математические модели, позволяющие оценить отказоустойчивость МСС при использовании однолинейной или многолинейной системы автоматизированного управления. Получены зависимости качества управления конфигурацией МСС и её отказоустойчивости от интенсивности потока отказов и восстановления элементов с учётом передачи информационных потоков потребителям с различными классами обслуживания.
ABSTRACT
In article the questions, estimations of influence of is probability-time characteristics of managerial process concerning mechanisms on fail safety of a multiservice communication network are considered. The mathematical models, allowing to estimate fail safety МСС are offered at usage of the one-linear or multilinear system of automated management. Dependences of quality of configuration management МСС and its fail safeties from intensity of a failure flow and recovery elements with the registration of transmission of information highways to customers with various classes of service are received.
Ключевые слова: функциональная отказоустойчивость; связность; система автоматизированного управления; однолинейная и многолинейная системы массового обслуживания.
Keywords: the functional fail safety; connectivity; automated management system; the one-linear and multilinear systems of mass service.
Зачастую показатели, по которым производится оценка структурной или функциональной отказоустойчивости мультисервисной сети связи (МСС), не учитывают характер её функционирования, как системы с автоматизированным управлением (САУ). При нарушениях конфигурации или связности МСС, САУ будет выполнять операции либо по восстановлению работоспособности её элементов, либо по изменению программы функционирования управляющих устройств с целью сохранения или модификации структуры МСС.
В основе этих действий должны лежать оценки, полученные в результате работы системы мониторинга. Если время реакции САУ на нарушение связности МСС не превысит допустимого времени доставки информационного сообщения (ИС) от отправителя к получателю (Тос), то следует считать, что состояние МСС не ухудшилось.
Таким образом, оценку конфигурации МСС H(G) следует производить по показателю, определяемому из выражения:
![]() , (1)
, (1)
где: Р1(t) — вероятность нарушения связности конфигурации сети (с учётом функциональных особенностей элементов сети);
Р2(t) — вероятность того, что общее время tp реакции системы управления (СУ) на устранение нарушений связности окажется больше допустимого среднего времени прохождения ИС через МСС, т. е. Р2=P (tp>![]() ).
).
Для оценки конфигурации МСС H(G) по данному показателю предположим, что:
· поток заявок на восстановление нарушений связности ее конфигурации, поступающий на САУ, является модифицированным простейшим;
· распределение длительностей задействования элементов САУ подчинено экспоненциальному закону с интенсивностью восстановления 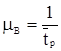 , где
, где ![]() — среднее время реакции САУ на устранение нарушений связности конфигурации МСС;
— среднее время реакции САУ на устранение нарушений связности конфигурации МСС;
· события, характеризующие нарушения связности конфигурации МСС, не зависят друг от друга;
· система управления МСС является системой массового обслуживания (СМО) с ожиданием.
Математические модели оценки отказоустойчивости МСС получим для случаев, когда САУ является однолинейной и многолинейной СМО [1].
Требование на устранение нарушений связности конфигурации МСС считается выполненным в том случае, когда САУ закончила необходимые операции по восстановлению ее связности за время tg = Тв.
Следовательно, вероятность Р2(t) может быть определена как вероятность того, что общее время tp пребывания такой заявки в САУ (период ожидания tож и время, затрачиваемое исполнительным устройством на устранение нарушений связности tус), не превысит заданное время ![]() . Для её нахождения воспользуемся моделью, предложенной в [1], согласно которой
. Для её нахождения воспользуемся моделью, предложенной в [1], согласно которой
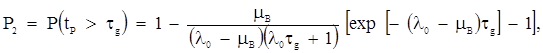 (2)
(2)
где: ![]() — интенсивность освобождений исполнительного устройства САУ;
— интенсивность освобождений исполнительного устройства САУ;
![]() — параметр потока требований на устранение нарушений конфигурации связности МСС;
— параметр потока требований на устранение нарушений конфигурации связности МСС;
![]() — допустимое время пребывания заявки в САУ. Предположим, что функциональные особенности элементов МСС не накладывают ограничений на ее структурную конфигурацию H(G). Тогда вероятность Р1 можно рассчитать по формуле
— допустимое время пребывания заявки в САУ. Предположим, что функциональные особенности элементов МСС не накладывают ограничений на ее структурную конфигурацию H(G). Тогда вероятность Р1 можно рассчитать по формуле
![]() (3)
(3)
В соответствии с показателем (1) структурная конфигурация сети H(G) определится выражением:
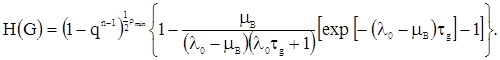 (4)
(4)
При учете функциональных ограничений элементов сети, расчет отказоустойчивости МСС H(Jij) в целом может быть представлен выражением:
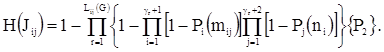 (5)
(5)
Таким образом, формулы (4) и (5) являются математическими моделями для определения структурной конфигурации МСС при централизованной системе управления.
С учетом полученных моделей по аналогии с (1) можно получить выражение для оценки отказоустойчивости сети с учетом пропускной способности направления связи (НС) для конкретной сети:
![]() , (6)
, (6)
где: ![]() — находится из выражения (5).
— находится из выражения (5).
Полученные модели позволяют оценивать отказоустойчивость МСС при наличии централизованной двухуровневой САУ, то есть при отсутствии элементов, обеспечивающих управление конфигурациями МСС в интересах потребителей различных классов обслуживания. Однако это является частным случаем.
В большинстве МСС в составе СУ имеется V1 исполнительных устройств одинаковой производительности (т. е. она является многолинейной СМО с распределенным управлением). Предположим, что поступает простейший поток заявок на устранение нарушений связности конфигурации с плотностью ![]() . Время обслуживания каждой такой заявки является случайной величиной tус, которая подчинена показательному закону распределения с параметром
. Время обслуживания каждой такой заявки является случайной величиной tус, которая подчинена показательному закону распределения с параметром 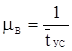 , где
, где ![]() — среднее время, необходимое одному из V1 исполнительных устройств САУ для обслуживания заявки. Если вновь прибывшая в САУ заявка застает все устройства занятыми, то она становится в очередь и ожидает обслуживания.
— среднее время, необходимое одному из V1 исполнительных устройств САУ для обслуживания заявки. Если вновь прибывшая в САУ заявка застает все устройства занятыми, то она становится в очередь и ожидает обслуживания.
Общее допустимое время tp пребывания заявки в САУ является случайным с показательным законом распределения и параметром 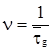 , где
, где ![]() — среднее допустимое время пребывания заявки в САУ.
— среднее допустимое время пребывания заявки в САУ.
Для многолинейной СМО [1], характеризующей в данном случае САУ, вероятность того, что общее время пребывания заявки в системе (устранение нарушений связности конфигурации МСС) превысит допустимое, можно определить по формуле:
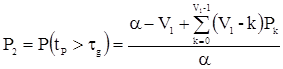 , (7)
, (7)
где 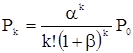 ;
;
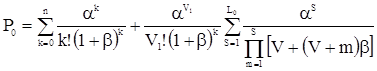 ;
;
![]() ,
, 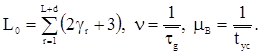
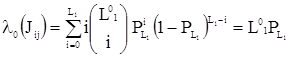 ,
,
где ![]() ;
;
![]() .
.
Тогда модель для оценки H(G) МСС с учетом (4) и (7) можно записать следующим образом:
 . (8)
. (8)
Для НС модель оценки H(Jij) приобретает вид:
 . (9)
. (9)
Для передачи информационных потоков потребителям с различными классами обслуживания отказоустойчивость МСС целесообразно оценивать для различных её конфигураций в единицах пропускной способности. Поэтому, по аналогии с (6), отказоустойчивость можно определить по формуле:
![]() , (10)
, (10)
где ![]() определяется на основе (9).
определяется на основе (9).
Полученные результаты дают возможность производить оценку отказоустойчивости МСС, управление которой осуществляет централизованная или распределенная СУ.
Как следует из выражения (1), H(G) различных конфигураций МСС определяется не только вероятностью её связности, но и вероятностно-временными параметрами СУ. Расчеты вероятностно-временных характеристик САУ показывают зависимость вероятности Р2 от превышения системой управления МСС допустимого времени tg в ходе устранения нарушений связности её конфигурации, от интенсивности ![]() потока повреждений элементов системы, интенсивности потока восстановлений
потока повреждений элементов системы, интенсивности потока восстановлений ![]() и допустимого времени восстановления ресурсов МСС tg.
и допустимого времени восстановления ресурсов МСС tg.
На рис. 1 изображен график зависимости вероятности Р2 от интенсивности ![]() , поступающих в САУ требований на устранение нарушений связности конфигураций МСС Р2 =f(l0) , построенный по результатам расчетов на модели (2).
, поступающих в САУ требований на устранение нарушений связности конфигураций МСС Р2 =f(l0) , построенный по результатам расчетов на модели (2).
Из графика следует, что качество реализации процесса управления конфигурациями сети снижается с увеличением интенсивности ![]() потока повреждения (или отказов) элементов МСС. Данное положение свидетельствует о важности решения задач, связанных с построением системы мониторинга.
потока повреждения (или отказов) элементов МСС. Данное положение свидетельствует о важности решения задач, связанных с построением системы мониторинга.
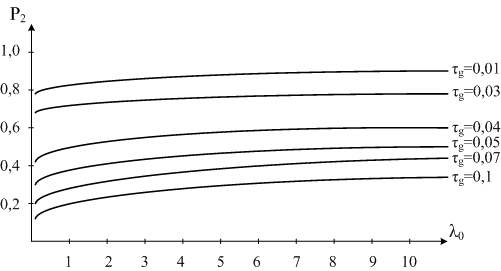
Рисунок 1. Зависимость качества управления конфигурацией МСС от интенсивности потока отказов элементов
Влияние на отказоустойчивость интенсивности потока ![]() обслуживания поступающих в САУ МСС требований на устранение нарушений связности её конфигураций, приведено на рис. 2.
обслуживания поступающих в САУ МСС требований на устранение нарушений связности её конфигураций, приведено на рис. 2.
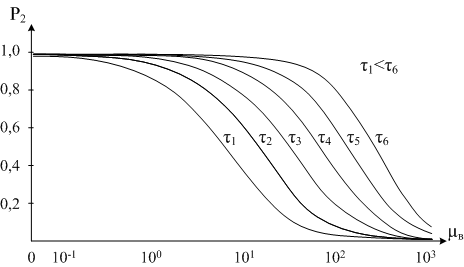
Рисунок 2. Зависимость отказоустойчивости системы от интенсивности восстановления её элементов
Параметром на кривых Р2 =f(![]() ) является значение времени tg. Кривые получены при постоянных значениях
) является значение времени tg. Кривые получены при постоянных значениях ![]() . Анализ этих кривых показывает, что при увеличении значений
. Анализ этих кривых показывает, что при увеличении значений ![]() вероятность превышения САУ допустимого времени tg резко падает. Однако при увеличении tg такой спад сдвигается вправо (в область увеличения значений величины
вероятность превышения САУ допустимого времени tg резко падает. Однако при увеличении tg такой спад сдвигается вправо (в область увеличения значений величины ![]() ). Из графика следует, что для обеспечения высоких показателей H(G) САУ должна обеспечивать высокую производительность при устранении нарушений связности конфигураций системы.
). Из графика следует, что для обеспечения высоких показателей H(G) САУ должна обеспечивать высокую производительность при устранении нарушений связности конфигураций системы.
Зависимость вероятности Р2 от допустимых значений времени tg показана на рис. 3. Из графика следует, что исследуемая вероятность Р2 уменьшается с ростом tg. Причем резкий спад кривых характерен для малых значений ![]() .
.
Приведенные расчеты подтверждают предположение, что чем выше уровень принятия решения на восстановление конфигураций МСС, тем сложнее выполнить требования по отказоустойчивости, так как в этом случае необходимо увеличить уровень агрегирования избыточной части системы.

Рисунок 3. Зависимость отказоустойчивости системы от требований к времени восстановления её элементов
Вместе с тем, чем ниже уровень принятия решения, тем больше количество аппаратно-программных элементов МСС, задействованных для решения проблемы отказоустойчивости, что приводит к повышению стоимости эксплуатации системы и росту потока отказов элементов. Это, с одной стороны, неминуемо ведет к увеличению количества персонала и средств технического уровня процесса восстановления, а с другой — к неизбежному снижению отказоустойчивого состояния МСС до уровня баланса потоков отказов и потоков восстановлений.
Список литературы:
1.Клейнрок Л. Вычислительные системы с очередями. /Перевод с английского под редакцией д-ра техн. наук Б.С. Цыбакова. М.: «МИР», 1979. — 600 с.
дипломов


Оставить комментарий