УСТОЙЧИВОСТЬ  ПОЧВЕННО-РАСТИТЕЛЬНЫХ  СИСТЕМ  С  ТОЧКИ  ЗРЕНИЯ  АВТОНОМНЫХ  ИМПУЛЬСНЫХ  ПРОЦЕССОВ

С алугин  Александр  Николаевич

д-р  с.-х.  наук,  канд.  физ.-мат.  наук,  профессор  кафедры  прикладной  математики  и  вычислительной  техники  Волгоградского  архитектурно-строительного  университета,  РФ,  г.  Волгоград

E-mail: 

STABILITY  SOIL-PLANT  SYSTEMS  IN  TERMS  OF  PULSE  PROCESSES  AUTONOMOUS

Salugin  Alexander

doctor  of  Agricultural  Sciences,  Candidate  of  Physics  and  Mathematics,  Professor,  Department  of  Applied  Mathematics  and  Computer  Science  Volgograd  Architectural  University,  Russia  Volgograd

АННОТАЦИЯ

Математическое  моделирование  использовалось  с  целью  выявления  условий  устойчивого  поведения  почвенно-растительных  систем  (ПРС).  Применен  алгоритм  распространения  автономного  импульса,  связанного  с  явлениями  передачи  энергии  и  информации  в  схеме  знакового  ориентированного  графа.  Определены  условия  устойчивости  ПРС

ABSTRACT

Mathematical  modeling  was  used  to  identify  the  conditions  for  sustainable  behavior  of  soil-plant  systems  (PRS).  Propagation  algorithm  applied  autonomous  momentum  associated  with  the  phenomena  of  the  transmission  of  energy  and  information  in  the  scheme  signed  directed  graph.  The  conditions  for  the  stability  of  ORS

Ключевые  слова:   автономный  импульсный  процесс;  знаковый  орграф;  математическое  моделирование;оптимизационная  задача;  сложные  системы.

Key  words:   self-switching  process;  signed  directed  graph;  mathematical  modeling;  optimization  problems;  complex  systems.

Исследования  динамики  биогеоценоза  почвенно-растительных  систем  (ПРС)  для  составления  прогнозов  требует  привлечения  разнообразных  методов  математического  моделирования.  Математический  метод  исследования  стал  одним  из  основных  при  решении  подобных  проблем,  а  возникшая  математическая  экология  в  настоящее  время  бурно  развивается  [2,  3].  Одной  из  ведущих  в  этой  дисциплине  является  проблема  устойчивости  экосистем.  Существовать  и  стабильно  функционировать  могут  только  устойчивые  экосистемы.  Стабильность  их  развития  определяется  заданными  максимальными  нагрузками,  превышение  которых  приводит  к  «экологической  катастрофе».  Человеческое  сообщество  сталкивается  с  проблемой  устойчивости,  когда  решает  вопросы  эксплуатации  природных  популяций  и  сообществ,  оценивает  пределы  загрязнений  среды,  определяет  допустимость  осуществления  тех  или  иных  природохозяйственных  мероприятий  и  т.  д.  Эти  оценки  адекватны  и  практически  значимыми  тогда,  когда  они  являются  количественными.  Математическая  модель  с  использованием  автономных  импульсных  процессов  разработана  и  описана  в  данной  работе  в  контексте  продолжения  наших  исследований  [1]  проблем  устойчивости  экосистем  вообще  и  ПРС  в  частности.  Автономность  означает  здесь  независимость  протекания  процесса  от  времени,  что  согласуется  с  многими  положениями  теории  диссипативных  систем  [2].  Знаковые  графы  успешно  применялись  для  решения  задач,  связанных  с  динамикой  систем,  с  параметрами  обеспечивающими  эту  устойчивость.  В  нашей  работе  мы  использовали  импульсный  процесс  как  основу  для  модели  эволюции  явлений  в  сложных  диссипативных  системах  типа  ПРС.  Коротко  остановимся  на  концепции  такого  подхода.

Пусть  эта  система  задана  в  виде  некоторого  множества  вершин  знакового  ориентированного  графа  G(V,X)  с  вершинами  V_i  ,  (i=1,2,…n),  влияющих  друг  на  друга  через  ориентированные  дуги  X_ij.  Взаимодействие,  описываемое  дугами,  направленными  от  влияющей  вершины  к  вершине,  на  которую  оказывается  влияние,  передается  посредством  автономного  импульса.  Вес  дуги  и  его  знак  отражают  степень  и  направленность  влияния  вершин  друг  на  друга:  влияние  позитивное,  если  дуга  положительна,  и  негативное  —  когда  отрицательна. 

В  начальном  состоянии  вершины  графа  задаются  вектором  начального  состояния  V(нач)_.  При  внешнем  действии  в  вершинах  графа  возникает  импульс  (начальный),  который  описывается  вектором  P(0).  Этот  вектор  импульса  будет  распространяться  по  системе  вершин  и  в  следующий  момент  наблюдения  станет  равным  P(1).  Таким  образом,  для  того,  чтобы  определить  состояние  экосистемы  в  любой  момент  времени  достаточно  знать  ее  начальное  состояние  и  импульс  внешнего  вмешательства.  Вектор  импульса  определяется  формулой  (1)  как  разность  между  векторами  весов  вершин  текущего  и  предыдущего  состояний:

Состояние  вершин  орграфа  в  любой  момент  времени  определяется  по  формуле  (2):

где  Aⁱ  —  i-я  степень  матрицы  смежности  орграфа.  Таким  образом,  для  того,  чтобы  определить  состояние  системы  в  любой  момент  времени  достаточно  знать  начальное  состояние  системы  и  начальный  импульс  внешнего  воздействия.  Распространения  импульса  моделирует  эволюцию  экосистемы  в  виде  устойчивого  или  устойчивого  развития.  Неустойчивость  характеризуется  возрастающими  во  времени  колебаниями  весов  вершин;  устойчивый  —  асимптотическим  приближением  к  фиксированным  значениям.

При  алгоритмизации  моделей  были  разработаны  классы  с  методами  матричных  операций,  вычислений  весов  вершин,  векторов  импульсов  и  оптимизации  весов  дуг.  Процесс  оптимизации  осуществлялся  поэтапно  методом  Монте-Карло  с  последовательным  уменьшением  области  поиска.  Координаты  случайных  точек  на  каждой  итерации  вычислялись  с  новой  области  поиска.  В  качестве  примера  рассмотрим  реальную  экосистему,  упрощённо  описывающую  сукцессионные  переходы  ПРС  Черных  земель  Калмыкии  [1],  описываемую  графом,  изображенном  на  рис.  1.  Здесь  отрицательные  дуги  означают  процесс  сукцессионного  перехода  на  более  низкий  уровень  (процесс  деградации  ПРС).  Распространение  начального  импульса  (увеличение  нагрузки  на  исходные  пастбища)  по  сукцессионной  схеме  переходов  (рис.1),  рассчитанное  по  (2),  приведено  на  рис.  2.

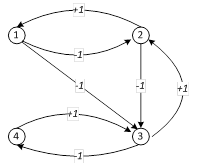
Рисунок  1.  Пример  почвенно-растительной  экосистемы  :  1  —  исходные  пастбища,  4  —  разбитые  пески,  2  и  3  —  полынные  и  —  сорнооднолетниковые  пастбища.  Векторы  начального  состояния  вершин  и  импульса:  V (нач)  =  (1  0  0  0),  P(0)  =  (1  0  0  0);  матрица  смежности: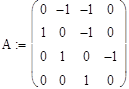 

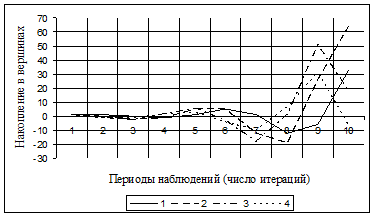
Рисунок  2.  График  изменения  значений  вершин  орграфа

Из  рисунка  видно,  что  накопление  в  вершинах  всех  типов  пастбищ  неограниченно  возрастает,  свидетельствуя  о  неустойчивости  экосистемы.  Результаты  моделирования,  таким  образом,  привели  к  тому,  что  система  с  подобными  исходными  данными  находится  в  состоянии  нестабильности,  а  сама  модель  не  является  неадекватной.  Это  произошло  потому,  что  исходные  значения  дуг  были  выбраны  из  качественных  оценок  сукцессионных  переходов  и  количественно  не  соответствуют  реальности.  Количественные  значения  переходов  в  матрице  смежности  модели,  соответствующие  стабильному  существованию  ПРС  были  получены  с  помощью  программы  оптимизации  с  ограничениями  изменения  весов  дуг    в  пределах  [0,±1].  Матрица  смежности  после  оптимизации:

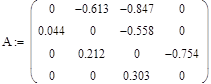
Видно,  что  коэффициенты  переходов  как  для  разрушения  (верхняя  наддиагональная  часть  матрицы  с  отрицательными  значениями),  так  и  для  восстановления  (нижняя  часть)  существенно  изменились.  На  рис.  3  приведены  данные  моделирования.  Видно  приведение  ПРС  к  стабильному  состоянию  через  несколько  начальных  этапов.  Модель  экосистемы  с  весами  дуг  орграфа,  стремящих  значения  весов  вершин  к  некоторому  постоянному  значению  свидетельствует  о  том,  что  полученные  данные  отражают  ситуацию  стабильного  существования  подобных  экосистем.

Приведенный  в  статье  пример  является  скорее  демонстрацией  того,  что  автономные  импульсные  процессы  адекватно  отражают  эволюцию  систем. 

Рисунок  3.  Накопление  значений  в  вершинах  для  оптимизированной  экосистемы

Полученные  результаты,  на  наш  взгляд,  являются  новыми  приложениями  графовых  математических  моделей  в  задачах  поиска  устойчивого  развития  сложных  диссипативных  систем  в  агроэкологии.

Исследования  диссипативных  систем  с  помощью  автономных  импульсных  процессов  эффективны  при  разработке  динамических  моделей  систем,  их  эволюции  и  составлении  прогнозов.  Не  смотря  на  очевидную  дискретность  импульсные  процессы  адекватно  описывают  непрерывное  изменение  состояний  систем  во  времени,  предоставляя  исследователю  возможность  подбирать  оптимальные  параметры  в  виде  соответствующих  весов  дуг  на  графавой  модели.  Это  служит  основой  для  принятия  правильных  управленческих  решений  в  использовании  биоресурсов.

Список  литературы:  

1.Кулик  К.Н.,  Салугин  А.Н.,  Сидорова  Е.А.  Динамическая  устойчивость  аридных  экосистем  //  Аридные  экосистемы.  —  2012.  —  Т.  18.  —  №  2(51).  —  С.  28—34. 

2.Робертс  Ф.С.  Дискретные  математические  модели  с  приложениями  к  социальным,  биологическим  и  экологическим  задачам:  Пер.  с  англ.  М.:  Наука.  1986.  —  496  с. 

3.Свирежев  Ю.М.,  Логофет  Д.О.  Устойчивость  биологических  сообществ.  Главная  редакция  физико-математической  лите­ратуры  изд-ва  «Наука»,  М.,  1978.  —  352  с.