ЭКСПЕРИМЕНТАЛЬНОЕ  ИССЛЕДОВАНИЕ  ПАРАЛЛЕЛЬНЫХ  АЛГОРИТМОВ  ИМИТАЦИИ  ОТЖИГА  ДЛЯ  ЗАДАЧИ  КОМПЛЕКТАЦИИ  ВЫЧИСЛИТЕЛЬНОЙ  СИСТЕМЫ  МИНИМАЛЬНОЙ  СТОИМОСТИ

Троценко  Роман  Владимирович

канд.  техн.  наук,  доцент  инженерно-технологической  академии  Южного  Федерального  Университета,  РФ,  г.  Таганрог

E -mail: 

" target="_blank">roman.trotsenko@gmail.com

Посашенко  Александр  Владимирович

учащийся  магистратуры  инженерно-технологической  академии  Южного  Федерального  Университета,  РФ,  г.  Таганрог

E-mail: 

EXPERIMENTAL  RESEARCH  OF  THE  PARALLEL  SIMULATED  ANNEALING  FOR  THE  MINIMAL  COST  COMPUTATIONAL  SYSTEM  DESIGN  TASK

Trotsenko  Roman

candidate  of  science,  assistant  professor  of  engineering  and  technology  academy  of  Southern  Federal  University,  Russia  Taganrog

Posashenko  Alexandr

post-graduate  student  of  engineering  and  technology  academy  of  Southern  Federal  University,  Russia  Taganrog

АННОТАЦИЯ

Задача  комплектации  вычислительной  системы  минимальной  стоимости  является  одной  из  основных  задач  проектирования  многопроцессорных  систем.  Имитация  отжига  —  один  из  наиболее  распространенных  методов  ее  решения.  В  статье  проведен  краткий  анализ  параллельных  алгоритмов  имитации  отжига  и  экспериментальная  оценка  их  эффективности  в  сравнении  с  централизованными  алгоритмами.

ABSTRACT

The  task  of  computational  system  design  with  minimal  cost  is  one  of  the  major  multiprocessor  system  design  tasks.  Simulated  annealing  is  one  of  the  most  widespread  methods  of  its  solving.  The  paper  contains  the  short  overview  of  the  parallel  simulated  annealing  algorithms.  The  simulation  results  and  the  numerical  evaluation  of  the  effectiveness  of  the  parallel  simulated  annealing  are  presented.

Ключевые  слова:  имитация  отжига;  параллельный  алгоритм.

Keywords:  simulated  annealing;  parallel  algorithm.

Задача  комплектации  вычислительной  системы  (ВС)  минимальной  стоимости  является  одной  из  наиболее  часто  решаемых  при  проектировании  многопроцессорных  систем.  В  общем  виде  задача  формулируется  следующим  образом  [1]:  для  заданного  комплекса  информационно  и  по  управлению  взаимосвязанных  задач,  заданной  архитектуры  вычислительной  системы,  а  также  заданного  ограничения  на  допустимое  время  вычислительного  процесса  выбрать  комплектацию  ВС  минимальной  стоимости.»  Под  стоимостью  понимают  вес  каждого  типа  процессоров,  который  необходимо  учитывать  при  выборе  оптимальной  комплектации.  Описываемая  задача  уловной  оптимизации  является  NP-сложной,  что  ставит  вопрос  о  выборе  метода  решения,  который  бы  позволил  получить  решение  за  приемлемое  время. 

Семейство  алгоритмов  имитации  отжига  являются  средством,  позволяющим  получать  хорошие  результаты  для  NP  сложных  задач  большой  размерности  благодаря  возможности  выхода  из  локальных  оптимумов  [3]. 

Алгоритмы  имитации  отжига  являются  итерационными  и  последовательными,  что  затрудняет  их  распараллеливание.  Тем  не  менее,  были  разработаны  методы  параллельного  выполнения  имитации  отжига,  позволившие  значительно  улучшить  скорость  и  точность  метода  [3].  В  данной  статье  проведено  экспериментальное  сравнение  асинхронного  параллельного  алгоритма  имитации  отжига  (рис.  1),  параллельного  алгоритма  с  синхронизацией  (рис.  2)  и  одной  из  адаптаций  асинхронного  алгоритма  для  условий  дефицита  времени  (рис.  3)  [2]. 

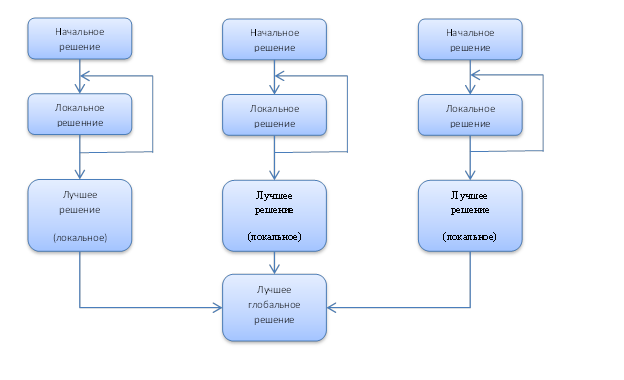
Рисунок  1.  Параллельный  асинхронный  алгоритм  имитации  отжига

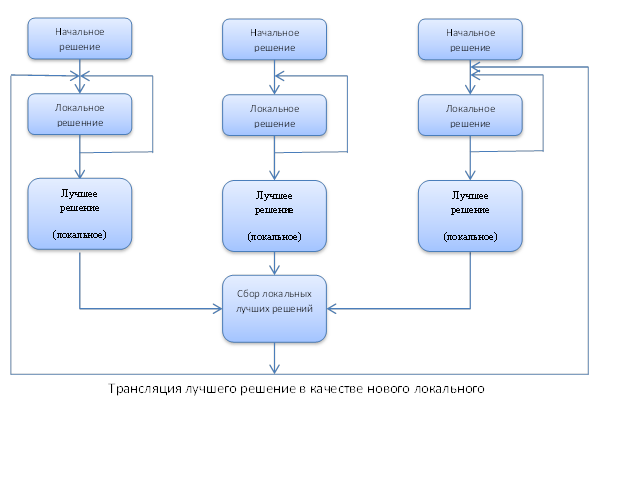
Рисунок  2.  Параллельный  алгоритм  имитации  отжига  с  синхронизацией

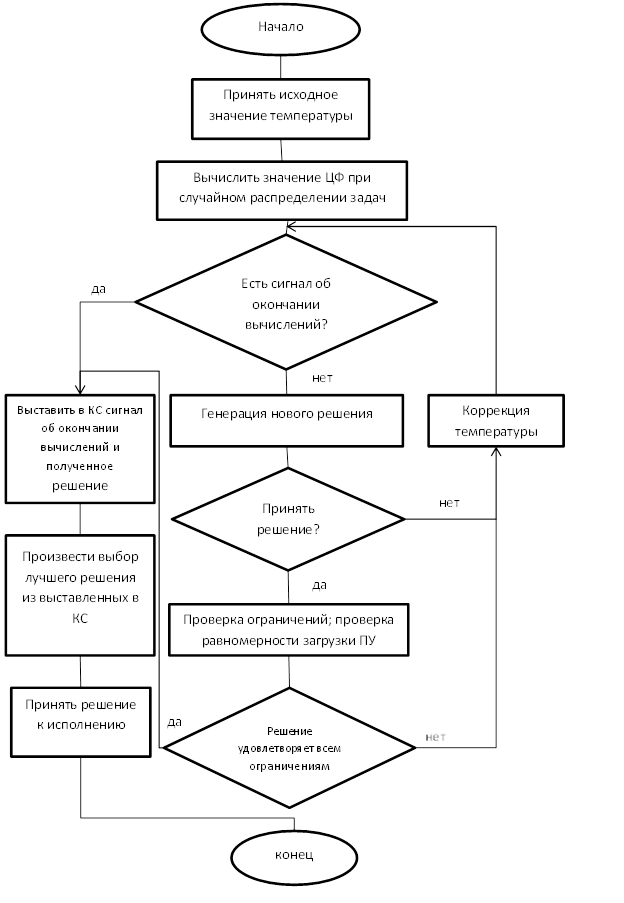
Рисунок  3.  Адаптация  асинхронного  алгоритма  формирования  конфигурации  ВС

Для  построения  алгоритма  имитации  отжига  для  конкретной  задачи  условной  оптимизации  прежде  всего  следует:

1.  Определить  представление  решения  X  и  операций  преобразования  текущего  решения.

2.  Разработать  стратегию  применения  операций  преобразования  текущего  решения.

3.  Выбрать  закон  понижения  температуры.

4.  Определить  функционал  F(  f  (X  ),  g  (X  ))  i  ,  используемый  для  оценки  качества  текущего  решения.

5.  Выбрать  критерий  останова  алгоритма.

Если  есть  g_i  не  вошедшие  в  функционал  F(  f  (X  ),  g  (X  ))  i  ,  то  после  применения  операций  преобразования  решения,  должно  получаться  решение,  удовлетворяющее  этим  ограничениям. 

Для  формирования  комплектации  ВС  минимальной  стоимости  перечисленные  задачи  были  решены  следующим  образом:

·     решением  Х  является  множество  процессорных  устройств  (ПУ)  и  распределение  по  ним  подзадач  основной  задачи;

·     новое  решение  формируется  путем  выбора  подмножества  ПУ  и  построения  для  них  оптимального  расписания  с  минимизацией  простоев.  Используется  алгоритм  составления  расписания  для  неоднородной  ВС  [1];

·     понижение  температуры  происходит  по  методу  «тушения»,  T_i=cT_j-1,  c=0,99;

·     качество  решения  оценивается  путем  вычисления  суммарной  стоимости  ПУ  с  учетом  ограничения  на  время  выполнения  задачи;

·     критерием  останова  является  достижение  конечной  температуры.

Следует  отметить,  что  метод  «тушения»  применяется  с  целью  ускорения  отжига,  но  при  этом  позволяет  «застрять»  при  поиске  в  локальном  минимуме.  При  этом  распараллеливание  имитации  отжига  с  изменением  температуры  по  этому  закону  наоборот,  повышает  вероятность  нахождения  глобального  минимума  целевой  функции.  Также  в  целях  повышения  информативности  результатов  эксперимента  в  качестве  критерия  останова  для  параллельных  алгоритмов  имитации  отжига  было  принято  следующее  правило:  останов  осуществляется  либо  по  достижении  нижней  границы  температуры  либо  по  достижению  оптимального  значения,  предварительно  найденного  методом  полного  перебора.  Использование  этого  правила  позволяет  произвести  оценку  эффективности  имитации  отжига,  поскольку  становится  очевидным  на  какой  итерации  уже  было  достигнуто  оптимальное  решение.

Были  проведены  вычисления  для  следующих  наборов  данных:

·     количество  ПУ,  на  которых  выполняется  параллельная  имитация  отжига  —  2…6;

·     количество  задач  в  графе  —  70;

·     количество  ПУ,  из  которых  выбираются  конфигурации  ВС  —  15.

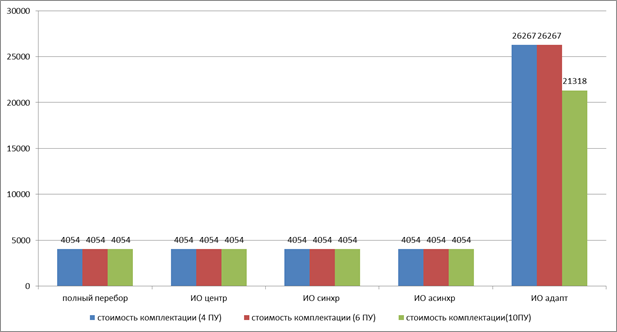
Рисунок  4.  Решения,  полученные  в  ходе  эксперимента

На  рис.  4  видно,  что  испытываемые  алгоритмы  пришли  к  решению,  полученному  полным  перебором  за  исключением  алгоритма,  адаптированного  для  использования  в  условиях  дефицита  времени.  Также  для  последнего  алгоритма  наблюдается  тенденция  улучшения  решения  с  увеличением  числа  параллельных  вычислителей,  что  объясняется  увеличением  количества  начальных  точек  имитации  отжига.

На  рис.  5  видно  также,  что  количество  параллельных  вычисляющих  устройств  позитивно  влияет  на  количество  вызовов  ЦФ:  с  увеличением  числа  вычислителей  имеется  тенденция  к  уменьшению  количества  вызовов  Цф,  что,  однако,  не  является  гарантией  подобного  уменьшения  времени  решения.  Особенно  это  актуально  для  имитации  отжига  с  синхронизацией,  поскольку  происходит  ожидание  вычисляющих  устройств  друг  другом  при  обмене  данными.

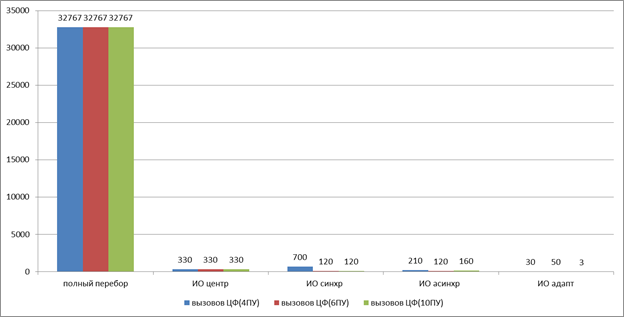
Рисунок  5.  Количество  вызовов  ЦФ

Подводя  итог  результатам  эксперимента,  можно  сделать  следующие  основные  выводы:

·     метод  имитации  отжига  является  одним  из  перспективных  методов  решения  NP-сложных  задач  (оптимальное  значение  функции  было  достигнуто  при  количестве  вызовов  целевой  функции  на  два  порядка  меньше  чем  при  поиске  полным  перебором);

·     при  увеличении  параллельных  вычисляющих  устройств  количество  вызовов  целевой  функции  имеет  тенденцию  к  уменьшению,  чего  нельзя  гарантировать  для  времени  вычислений  за  счет  обмена  результатами;

·     в  случае,  когда  в  качестве  критерия  останова  выступает  достижение  решения,  удовлетворяющего  ограничениям,  возможно  получение  результата  за  малое  количество  итераций,  но  посредственного  качества  (рис.4).

Список  литературы:

1.Барский  А.Б.  Параллельные  процессы  в  вычислительных  системах:  планирование  и  организация.  М.:  Радио  и  связь,  1990.

2.Клименко  А.,  Мельник  Э.  Задача  реконфигурирования  распределенных  информационно-управляющих  систем.  В  мире  научных  открытий.  —  №6(42).  —  2013.  —  С.  245—260.

3.Busetti  F.,  Simulated  annealing  overview.  2003.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://citeseer.uark.edu:8080/citeseerx/viewdoc/summary;jsessionid=9F958F3AD8ACB341A84315A737883592?doi=10.1.1.66.5018)