СПОСОБ  СНИЖЕНИЯ  ПОГРЕШНОСТИ  ОЦЕНКИ  ЧАСТОТЫ  ПЕРИОДИЧЕСКОГО  ТРЕНДА  ПО  ЧИСЛАМ  ПЕРЕСЕЧЕНИЯ  НУЛЕВОГО  УРОВНЯ

Левенец  Алексей  Викторович

канд.  техн.  наук,  доцент  кафедры  автоматики  и  системотехники  Тихоокеанского  государственного  университета,  РФ,  г.  Хабаровск

E-mail: 

THE  WAY  OF  DECREASE  OF  A  ERROR  OF  ESTIMATING  OF  FREQUENCY  OF  THE  PERIODIC  TREND  BY  ZERO-CROSSING  METHOD

Levenets  Alexey  Viktorovich

candidate  of  Science,  assistant  professor  of  faculty  of  automatics  and  system  engineering  of  Pacific  National  University,  Russia  Khabarovsk

АННОТАЦИЯ

В  статье  предлагается  способ  снижения  погрешности  оценки  частоты  периодического  тренда  измерительного  сигнала  на  базе  чисел  пересечения  сигналом  нулевого  уровня.  Суть  способа  заключается  в  определении  области  значений  сигнала,  где  он  условно  принимается  равным  нулю.  Приведены  результаты  исследования  предложенного  способа  на  моделях  измерительных  сигналов  с  периодическими  трендами  разных  типов.  Показано,  что  предложенный  способ  позволяет  снизить  погрешность  оценки  частоты  периодического  тренда  в  области  низких  относительных  частот.

ABSTRACT

In  paper  the  way  of  decrease  of  an  error  of  estimating  of  frequency  of  a  periodic  trend  by  zero-crossing  method  is  offered.  The  way  is  based  on  defining  ranges  of  values  of  the  signal,  where  it  is  conditionally  assumed  equal  to  zero.  Results  of  research  of  the  proposed  method  with  models  of  measuring  signals  with  periodic  trends  of  different  types  are  submitted.  It  is  shown  that  the  offered  method  allows  to  decreasing  of  an  error  of  a  estimating  of  frequency  of  a  periodic  trend  for  low  relative  frequencies  area. 

Ключевые  слова:  тренд;  измерительный  сигнал;  пересечение  нуля.

Keywords:   trend;  measurement  signal;  zero-crossing.

Числа  пересечения  сигналом  нулевого  уровня  обладают  рядом  свойств,  позволяющих  использовать  их  для  анализа  сигнала,  в  том  числе,  в  частотной  области.  Возможность  применения  свойств  таких  чисел  для  спектрального  анализа  показал  Б.  Кедем.  Так,  в  его  работах  было  доказано,  что  если  анализируемый  процесс  обладает  доминирующей  составляющей  с  частотой  f_д,  то  число  пересечений  нулевого  уровня  (ЧПН)  будет  стремиться  к  числу,  соответствующему  этой  частоте  [1].  Таким  образом,  применяя  к  исследуемому  сигналу  ряд  линейных  фильтров,  с  различными  частотами  среза,  и  определяя  после  каждой  фильтрации  через  ЧПН  частоту  доминирующей  составляющей,  можно  определить  наличие  в  анализируемом  сигнале  периодичности  с  некоторой  частотой. 

В  качестве  фильтров  было  предложено  использовать  простые  повторно-разностные  и  повторно-суммирующие  фильтры.  Реализация  первого  порядка  таких  фильтров  сводится  к  последовательному  вычитанию  (сложению)  соседних  отсчетов  исходной  последовательности  данных,  причем  применение  такой  операции  к  уже  отфильтрованной  последовательности  является  реализацией  фильтра  второго  порядка  и  т.  д.  Отличительной  особенностью  описанных  фильтров  является  простота  реализации  и,  как  следствие,  низкая  требовательность  к  вычислительным  затратам

Так  как  нули  сигнала  связаны  со  спектральной  функцией  анализируемого  сигнала,  в  [2]  было  предложено  использовать  этот  факт  для  грубого  спектрального  анализа  сигнала.  Для  этого  к  исходному  сигналу  последовательно  применялись  ПР  и  ПС  фильтры  в  различных  сочетаниях  (максимальный  порядок  фильтров  при  этом  ограничивается)  и  производился  подсчет  ЧПН  для  каждого  сочетания  таких  фильтров.  Совокупность  ЧПН,  полученную  после  применения  к  сигналу  ряда  простейших  фильтров  можно  рассматривать  как  некоторое  подобие  спектральной  функции,  которое  в  [2]  предложено  называть  «квазиспектр».

Проведенные  исследования  показали  принципиальную  возможность  их  использования  для  выявления  и  оценки  частоты  периодического  тренда  в  измерительных  данных  [2].  Более  подробно  эта  возможность  была  исследована  в  работе  [3],  где  было  показано,  что  одним  из  ограничений,  свойственных  такому  методу  является  его  высокая  погрешность  определения  частоты  периодического  тренда  на  краях  относительного  частотного  диапазона,  особенно  в  области  низких  относительных  частот.  Этот  факт  объясняется  высокой  чувствительностью  метода  к  помехам  в  области  пересечения  сигналом  нулевого  уровня,  а  также  пологими  передаточными  характеристиками  фильтров  [2]. 

Для  снижения  погрешности  оценки  частоты  периодического  тренда  в  области  низких  относительных  частот  можно  предложить  виртуальную  нелинейную  обработку  анализируемого  сигнала,  заключающуюся  в  том,  что  вводится  понятие  «ширина  нулевого  уровня»  (ШНУ),  т.  е.  задается  диапазон  значений  анализируемого  сигнала,  в  котором  он  условно  считается  равным  нулю  (рис.  1). 

Рисунок  1.  Пояснение  к  предлагаемому  способу  снижения  погрешности

Очевидно,  что  при  обычном  подсчете  ЧПН  оценка  частоты  периодичности  будет  существенно  искажена  действующими  помехами.  В  том  же  случае,  когда  вводится  отличная  от  нуля  ШНУ,  оценка  становится  существенно  более  точной,  т.  к.  формально  шумовая  составляющая  не  пересекает  нулевого  уровня.  Такую  обработку  с  точки  зрения  квазиспектра  можно  считать  дополнительным  низкочастотным  фильтром,  снижающим  влияние  высокочастотных  помех  на  оценку  частоты  низкочастотного  периодического  тренда.  Следует  отметить,  что  предлагаемая  обработка  используется  только  при  подсчете  ЧПН  и  не  применяется  к  самому  исследуемому  сигналу. 

Для  оценки  эффективности  предлагаемого  способа  исследования  проводились  на  модели  измерительного  сигнала  в  виде  аддитивной  смеси  периодического  сигнала  с  заданной  частотой  и  шума  с  равномерным  распределением.  Выбор  типа  шума  был  произвольным,  т.  к.  в  [3]  было  показано,  что  этот  параметр  не  оказывает  практического  влияния  на  результаты  оценки  частот.  Отношение  сигнал/шум  принималось  равным  1,0.

В  качестве  периодического  тренда  рассматривались  синусоида,  меандр,  пилообразный  и  треугольный  сигналы.  Так  как  объем  выборки  практически  не  сказывается  на  величине  относительной  погрешности,  далее  в  работе  приведены  результаты  для  объема  в  512  выборок.  Как  и  в  [3],  при  определении  квазиспектра  использовались  фильтры  не  выше  девятого  порядка,  а  результаты  усреднялись  по  десяти  реализациям.  Величина  ШНУ  задавалась  в  процентах  от  максимального  уровня  исследуемого  сигнала,  причем  нулевое  значение  соответствует  традиционному  пониманию  нулевого  уровня.

На  рис.  2  приведены  зависимости  относительной  погрешности  определения  частоты  δ_f  для  различных  типов  периодического  тренда  и  различных  значений  ширины  нулевого  уровня.  На  рисунке  цифрами  обозначено:  1  —  результаты  в  случае  ШНУ  =  0;  2  —  для  ШНУ  =  10  %;  3  —  для  ШНУ  =  20  %;  4  —  для  ШНУ  =  40  %.  На  рисунке  показано  поведение  погрешности  оценки  частоты  в  низкочастотной  области,  т.  к.  предлагаемый  способ  не  влияет  на  погрешности  в  остальной  частотной  области.

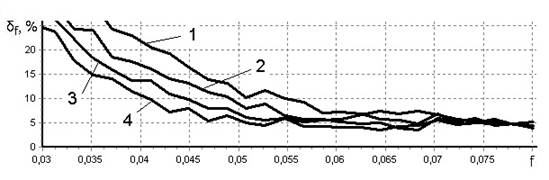
а)  синусоидальный

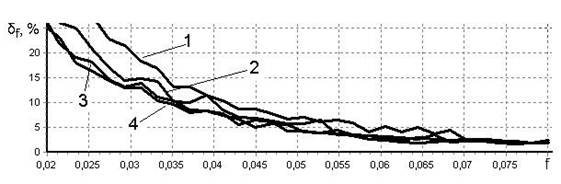
б)  меандр

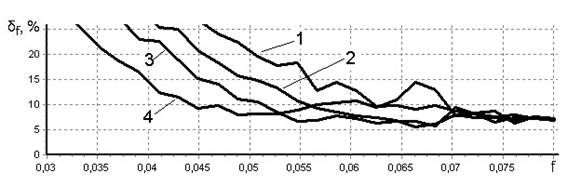
в)  треугольный

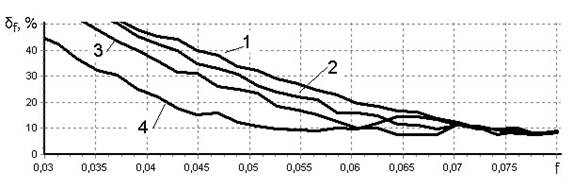
г)  пилообразный 

Рисунок  2.  Относительная  погрешность  определения  частоты  для  разных  типов  периодического  тренда

Полученные  результаты  показывают,  что  предлагаемый  способ  снижения  погрешности  приводит  к  существенному  снижению  погрешности  в  диапазоне  относительных  частот  0,0…0,07  для  всех  типов  тренда.  Следует  отметить,  что  на  рисунках  не  отображен  диапазон  0  …  0,02  в  силу  того,  что  погрешность  в  этой  области  хотя  и  существенно  снижается,  но  остается  в  области,  далекой  от  практического  применения. 

В  целом,  практически  для  всех  типов  тренда  можно  отметить  снижение  погрешности  на  5  %  и  более,  причем  наиболее  существенное  снижение  можно  отметить  для  трендов  типа  «пила»  и  «треугольник».  Так,  для  тренда  типа  «пила»  погрешность  оценки  в  диапазоне  частот  0,03…0,05  при  ШНУ  40  %  снижается  примерно  на  20  %,  однако  при  увеличении  частоты  тренда  эффективность  предлагаемого  способа  падает,  а  на  частоте  ≈0,065  снижается  практически  до  нуля.  Для  тренда  типа  «треугольник»  снижение  погрешности  несколько  меньше  и  составляет  на  частоте  0,045  и  ШНУ  40  %  примерно  18  %,  однако  уже  с  частоты  ≈0,05  эффективность  способа  начинает  снижаться  и  на  частоте  ≈0,06  величины  погрешностей  практически  совпадают  со  значениями  погрешности  без  обработки.

Следует  отметить  особенность  поведения  погрешности  для  тренда  типа  «меандр».  Для  этого  тренда  предлагаемый  способ  при  величине  ШНУ  10—20  %  обеспечивает  снижение  погрешности  примерно  на  5  %  в  диапазоне  относительных  частот  0,03  …  0,07,  причем  увеличение  ШНУ  приводит  к  существенному  снижению  погрешности  только  в  области  относительных  частот  менее  0,03.  Этот  факт  можно  объяснить  хорошей  чувствительностью  исследуемого  способа  оценки  частоты  к  тренду  типа  «меандр»,  причем  погрешности  для  этого  типа  тренда  существенно  меньше,  чем  у  остальных  типов  тренда,  даже  без  предлагаемого  способа  снижения  погрешности.

Для  синусоидального  тренда  снижение  погрешности  в  результате  применения  предлагаемого  способа  больше,  чем  для  тренда  типа  «меандр»  и  в  диапазоне  частот  0  …  0,047  составляет  ≈12—15  %.  На  частотах  0,06  и  более  эффективность  предлагаемого  способа  снижения  погрешности  близка  к  нулю.

Следует  отметить,  что  увеличение  ШНУ  более  20  %  для  трендов  типа  «меандр»  и  «синусоида»  не  приводит  к  существенному  улучшению  ситуации,  в  отличие  от  остальных  типов  тренда,  для  которых  снижение  погрешности  на  относительных  частотах  0  …  0,05  при  ШНУ  более  30  %  достигает  15—25  %.  Тем  не  менее,  следует  отметить,  что  при  ШНУ  40  %  и  более  для  всех  типов  тренда  наблюдается  увеличение  погрешности  оценки  частоты,  чем  при  меньших  значениях  ШНУ.

Проведенные  исследования  показали,  что  снижение  погрешности  за  счет  использования  предложенного  метода  происходит  также  и  при  снижении  ОСШ  до  значения  0,75,  однако  в  этом  случае  полученный  эффект  представляет  меньшую  практическую  значимость.

Таким  образом,  предложенный  способ  снижения  погрешности  оценки  частоты  периодического  тренда  позволяет  уменьшить  относительную  погрешность  оценки  в  частотном  диапазоне  0  …  0,06  не  менее  чем  на  5  %,  причем  для  тренда  типа  «меандр»  предложенный  способ  обладает  несколько  меньшей  эффективностью.  Также  следует  отметить,  что  предложенный  способ  легко  реализуется  и  не  требует  существенного  увеличения  вычислительных  затрат. 

Список  литературы:

1.Кедем  Б.  Спектральный  анализ  и  различение  сигналов  по  пересечениям  нуля  //  ТИИЭР.  т.  74.  —  1986.  —  №  11.  —  С.  6—24.

2.Левенец  А.В.,  Чье  Ен  Ун,  Иванов  В.Э.  Первичная  обработка  данных.  Оценка  спектра,  сжатие,  распознавание.  Saarbrücken:  LAP  LAMBERT  Academic  Publishing,  2012.  —  160  c.

3.Левенец  А.В.  Оценка  частоты  периодического  тренда  в  измерительном  сигнале  //  XХI  Международная  заочная  научно-практическая  конференция  «Технические  науки  —  от  теории  к  практике»,  Новосибирск,  2013.  —  С.  167—173.