ПРИМЕНЕНИЕ  АЛЬТЕРНИРУЮЩЕГО  МЕТОДА  ШВАРЦА  К  РЕШЕНИЮ  ПОЛИКОНТАКТНЫХ  ЗАДАЧ  ТЕОРИИ  УПРУГОСТИ

Яковлев  Максим  Евгеньевич

аспирант,  ассистент  кафедры  ФН-2,  МГТУ  им.  Н.Э.  Баумана,  РФ,  г.  Москва

E-mail: 

APPLICATION  OF  SCHWARZ  ALTERNATING  METHOD  TO  THE  SOLUTION  OF  POLYCONTACT  PROBLEMS  OF  ELASTICITY

Maxim  Yakovlev

graduate  student,  assistant,  Moscow  State  Technical  University,  Russia  Moscow

Аннотация

В  работе  рассмотрены  особенности  алгоритма  численного  решения  поликонтактных  задач  механики  деформируемого  твёрдого  тела  в  сложных  двухмерных  областях.  Решение  построено  в  рамках  конечно-элементной  технологии  на  основе  альтернирующего  метода  Шварца.  Метод  состоит  в  попеременном  выполнении  на  контактных  поверхностях  силовых  и  кинематических  граничных  условий.  Проведён  анализ  напряжённо-деформированного  состояния  столба  тепловыделяющих  элементов.

ABSTRACT

The  paper  discusses  the  features  of  the  algorithm  of  numerical  solution  of  polycontact  problems  of  solid  mechanics  in  complex  two-dimensional  fields.  The  solution  is  constructed  in  the  framework  of  finite  element  technology  based  on  the  Schwarz  alternating  method.  The  method  consists  of  alternating  between  fulfilling  the  power  and  the  kinematical  boundary  conditions  on  the  contact  surfaces.  The  stress-strain  state  of  the  fuel  elements  column  is  analyzed.

Ключевые  слова:  контактное  взаимодействие  упругих  тел;  метод  Шварца;  метод  конечных  элементов;  поликонтактное  взаимодействие;  итерационное  решение

Keywords:  Contact  interaction  of  elastic  bodies;  the  Schwartz  method;  finite  element  method;  polycontact  interaction;  the  iterative  solution

Многие  ответственные  узлы  и  элементы  конструкций  объектов  энергетического  оборудования,  авиационной,  аэрокосмической,  наземной  и  морской  транспортной  техники  работают  в  условиях  контактного  взаимодействия.  Для  правильной  оценки  их  ресурса  и  надежности  необходимо  знать  напряженно-деформированное  состояние,  которое  можно  определить,  решив  соответствующую  контактную  задачу.  Таким  образом,  контактные  задачи  являются  одними  из  центральных  в  механике  деформируемого  твердого  тела,  так  как  контакт  —  это  основной  метод  приложения  нагрузок  к  деформируемому  телу,  кроме  того,  концентрация  напряжений  в  зоне  контакта  часто  инициирует  разрушение  материала. 

Весьма  перспективным  для  решения  контактных  задач  является  применение  альтернирующего  метода  Шварца,  основанном  на  принципе  поочередности.  Преимущества  этого  метода  состоят  в  том,  что  не  требуется  согласовывать  построение  узлов  конечно-элементных  моделей  на  поверхностях  контакта  и  переформировывать  матрицы  систем  линейных  алгебраических  уравнений  в  процессе  итерационного  уточнения  границ  зон  контакта,  что  особенно  важно  в  случае  большого  числа  контактирующих  тел.

Математическая  формулировка  контактной  задачи  теории  упругости  включает:  уравнения  равновесия

  ;      (1)

граничные  условия

;                     (2)

  ;        (3)

соотношения  Коши

;  (4)

и  определяющие  уравнения  в  форме  закона  Гука

                  (5)

здесь  D  —  матрица  Гука,    —  вектор  напряжений,    —  вектор  деформации,    —  вектор  начальной  деформации  (например,  обусловленной  температурным  воздействием)    —  вектор  заданных  перемещений  точек  поверхностей  ,    —  компоненты  распределенной  нагрузки    на  поверхностях  .

Кроме  того,  на  каждой  поверхности  контакта    должны  быть  выполнены  условия  контактного  взаимодействия:  кинематическое

                             (6)

и  силовое

,                                   (7)

где:  ,    —  проекции  перемещений  граничных  точек  на  внешнюю  нормаль  к  границе  тела    (); 

  —  начальное  расстояние  по  нормали  между  граничными  точками; 

,    —  составляющие  поверхностных  сил  по  внешней  нормали  к  границе  тела  .  Соотношения  (6)  и  (7)  соответствуют  случаю,  когда  трение  не  учитывается.

Для  решения  контактной  задачи  (1)—(7)  был  использован  алгоритм,  основанный  на  альтернирующем  методе  Шварца  [2—4].  Данный  метод  является  итерационным.  Рассмотрим  его  работу  в  случае  двух  контактирующих  тел    и  .  Для  численного  решения  задач  теории  упругости  используется  метод  конечных  элементов  [1].  Пронумеруем  узлы  контактных  поверхностей    и    и  введем  в  рассмотрение  векторы  —    и  ,  ,  первый  из  которых  составлен  из  компонент  перемещений    и    узлов,  расположенных  на  контактной  поверхности  ,  а  второй  —  из  компонент    и    узловых  сил  тех  же  узлов.             

В  первом  шаге  на  контактных  поверхностях  тел    и    соответственно    и    задают  начальные  перемещения    и  ,  которые  имеют  смысл  дополнительных  кинематических  условий.  Далее  решают  независимо  две  подобные  задачи  теории  упругости  для  тел    и  .  Затем  вычисляют  поверхностные  силы    и    на  контактных  поверхностях    и    и  корректируют  их  так,  чтобы  выполнялись  силовые  контактные  условия  (7),  по  формуле

  (8)

здесь    —  итерационный  параметр,      —  узел,  лежащий  на  контактной  поверхности    тела  ,  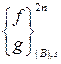  —  вектор  контактных  узловых  сил  сходственной  точки  ,  лежащей  на  контактной  поверхности    тела  .

Во  втором  шаге  на  контактных  поверхностях    и    задают  силовые  контактные  условия,  в  качестве  которых  используют  скорректированные  поверхностные  силы    и  ,  и  вновь  решают  независимо  задачи  теории  упругости  отдельно  для  тел    и  .  По  результатам  полученных  решений,  выполняют  коррекцию  компонент  векторов  перемещений    и    соответственно  точек  контактных  поверхностей    и    с  тем,  чтобы  выполнялись  кинематические  условия  контактного  взаимодействия  (6),  по  формуле

  (9)

где:    —  итерационный  параметр, 

    —  узел,  лежащий  на  контактной  поверхности    тела  , 

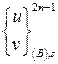  —  вектор  перемещений  сходственной  точки  ,  лежащей  на  контактной  поверхности    тела  . 

Скорректированные  перемещения  точек  контактных  поверхностей    и    рассматривают  в  качестве  новых  кинематических  граничных  условий  на  геометрически  измененных  поверхностях  контакта    и    и  вновь  решают  независимо  задачи  теории  упругости  отдельно  для  тел    и  .  Вопрос  выбора  итерационных  параметров  рассматривался,  в  частности,  в  работах  [2,  3].

В  случае  большего  количества  (n)  контактирующих  тел  метод  модифицируется  следующим  образом.  В  первом  шаге  на  всех  контактных  поверхностях  тел  задаются  перемещения    и  решаются  n  отдельных  задач  теории  упругости.  Во  втором  шаге  часть  этих  кинематических  граничных  условий  (на  подмножестве    множества  контактных  поверхностей  )  заменяется  скорректированными  силовыми  аналогично  случаю  двух  тел,  а  часть  (на  подмножестве  )  остается  прежними,  таким  образом,  чтобы  для  любого  тела  соответствующая  задача  теории  упругости  имела  единственное  решение,  и  снова  решаются  n  отдельных  задач.  В  третьем  шаге  кинематические  граничные  условия  на  контактных  поверхностях  из  множества    заменяются  на  скорректированные  силовые  по  формуле  (8),  а  силовые  граничные  условия  на  поверхностях  из  множества    —  на  скорректированные  кинематические  по  формуле  (9).  Далее  корректировка  кинематических  и  силовых  граничных  условий  чередуется  таким  же  образом  до  сходимости  на  всех  поверхностях.

Важно  отметить,  что  с  увеличением  количества  контактирующих  тел  значительно  возрастает  зависимость  скорости  сходимости  от  выбранного  начального  приближения.  Хороший  результат  во  многих  случаях  дает  использование  в  качестве  начального  приближения  решения  задачи  для  единого  твердого  тела  достаточно  сходной  формы  при  тех  же  кинематических  и  силовых  граничных  условиях  и  температурном  воздействии.  Такое  решение  часто  может  быть  легко  получено  аналитически  и  при  этом  дает  качественное  изменение  характера  сходимости,  приводящее  к  увеличению  скорости  сходимости  в  несколько  раз.  Так,  в  приведенном  ниже  примере  при  поиске  начального  приближения  система  тел  заменялась  единым  телом  прямоугольного  сечения.

На  основе  разработанного  алгоритма  был  создан  комплекс  прикладных  программ  для  решения  термоупругих  контактных  задач.  Для  проверки  работоспособности  программного  комплекса  было  выполнено  численное  решение  ряда  задач,  имеющих  известное  аналитическое  решение  [3].  В  качестве  примера  поликонтактного  взаимодействия  был  проведен  модельный  расчет  напряженно-деформированного  состояния  столба  тепловыделяющих  элементов.  Температура  во  всех  четырех  телах  распределена  одинаково  и  линейно  убывает  вдоль  оси  абсцисс.  Сверху  приложена  распределенная  нагрузка  МПа.  На  рис.  1  приведено  полученное  распределение  напряжений  вдоль  оси  ординат.

Рисунок  1.  Распределение  компоненты  тензора  напряжения    (МПа)

Выводы:

Разработан  алгоритм  решения  поликонтактных  задач  на  основе  альтернирующего  метода  Шварца  и  создан  комплекс  прикладных  программ.  Выполненный  цикл  численных  исследований  контактного  взаимодействия  термоупругих  тел,  имеющих  сложное  геометрическое  оформление,  показал  достаточно  высокую  эффективность  разработанного  алгоритма  и  реализующего  его  программного  кода.

Список  литературы:

1.Зенкевич  О.  Метод  конечных  элементов  в  технике.  М.:  Мир,  1975.  —  542  с.

2.Можаровский  Н.С.,  Качаловская  Н.Е.  Приложение  методов  теории  пластичности  и  ползучести  к  решению  инженерных  задач  машиностроения:  В  2  т.  Т.  2:  Методы  и  алгоритмы  решения  краевых  задач.  К.:  Выща  школа,  1991.  —  287  с.

3.Станкевич  И.В.,  Яковлев  М.Е.,  Си  Ту  Хтет.  Разработка  алгоритма  контактного  взаимодействия  на  основе  альтернирующего  метода  Шварца  //  Вестник  МГТУ  им.  Н.Э.  Баумана.  Сер.  Естественные  науки.  2011.  Спец.  вып.  Прикладная  математика.  —  С.  134—141.

4.Цвик  Л.Б.  Принцип  поочередности  в  задачах  о  сопряжении  и  контакте  твердых  деформируемых  тел.  //  Прикл.  Мех.  —  1980  —  т.  16,  Ш  I  —  С.  13—18.