Статья опубликована в рамках: XXVIII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 27 ноября 2013 г.)
Наука: Технические науки
Секция: Приборостроение, метрология, радиотехника
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МЕТОД ФОКУСИРОВКИ ДЛЯ ИЗМЕРЕНИЯ ГЕОМЕТРООПТИЧЕСКИХ ПАРАМЕТРОВ СВЕТОВОДОВ
Андросик Андрей Борисович
канд. техн. наук, доцент МГОУ, РФ, г. Москва
Воробьев Сергей Андреевич
канд. техн. наук, профессор МГОУ, РФ, г. Москва
Мировицкая Светлана Дмитриевна
канд. техн. наук, доцент МГОУ, РФ, г. Москва
E-mail:
THE FOCUSING METHOD FOR MEASUREMENT OF GEOMETRICAL AND OPTICAL PARAMETERS OF WAVEGUIDES
Andrey Androsik
candidate of Technical Sciences, Associate Professor of MSOU, Russia Moscow
Sergei Vorobev
candidate of Technical Sciences, Professor of MSOU, Russia Moscow
Svetlana Mirovitskaya
candidate of Technical Sciences, Associate Professor of MSOU, Russia Moscow
АННОТАЦИЯ
Рассмотрены особенности одного из наиболее удобных неразрушающих методов измерения основных геометрооптических характеристик волоконных световодов. Получено выражение для нахождения распределения показателя преломления. Приведены оценки точности измерений методом фокусировки.
ABSTRACT
The peculiarities of one of the most convenient non-destructive methods of measuring geometrical and optical parameters of optical fibers are reviewed. Expression for the location of the distribution of the refractive index is obtained. The accuracy of measurements by the focusing method is estimated.
Ключевые слова: волоконный световод; метод фокусировки; профиль показателя преломления; узкий пучок.
Keywords: the fiber waveguide; the focusing method; the profile of the refractive index; narrow beam.
Наиболее важными характеристиками волоконных световодов (ВС) являются геометрооптические — диаметр сердцевины, внешняя форма, распределение показателя преломления. При этом ВС должен быть однородным по всей длине. Отсюда вытекает необходимость разработки оперативных и высокоточных методов измерения формы и распределения показателя преломления оптических волокон (ОВ).
Метод фокусировки [1, с. 52, 2, с. 75] удобен для точного контроля профиля показателя преломления заготовок, а также оптических волокон и основан на фокусирующих свойствах сердцевины волокна, представляющей собой цилиндрическую линзу, при поперечном его освещении.
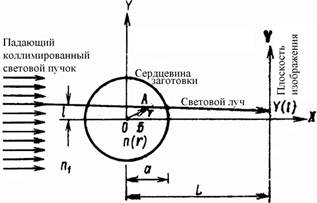
Рисунок 1. Схема измерения параметров ОВ методом фокусировки
На сердцевину под прямым углом к оси волокна, помещенного в иммерсионную жидкость, направляется параллельный некогерентный световой пучок постоянной интенсивности. Луч, входящий в сердцевину волокна (или заготовки) на расстоянии l от оптической оси (рис. 1), преломляется и выходит из сердцевины под углом, отличающимся от угла входа. В плоскости изображения волокна зондирующий луч попадает в точку на расстоянии y=y(l) от оптической оси. Количественная связь профиля показателя преломления ∆n и координаты y(t) описывается для параксиальных лучей уравнением d2y/dx2= (l/n1) ∂n/∂y, откуда наклон луча dy/dx на выходе из сердцевины определяется интегрированием:
![]() . (1)
. (1)
Для рассматриваемых осесимметричных объектов распределение показателя преломления является функцией радиальной координаты r, связанной с переменной интегрирования x соотношением![]() , т. е.
, т. е. ![]() , а следовательно, (dn/dy) = (∂n/∂r) (∂r/∂y) = (∂n/∂r) (y/r) ≈ (∂n/∂r) (l/r). Внутри сердцевины волокна наблюдается слабое отличие у от l. Угол наклона луча с учетом (1) выражается интегральным соотношением
, а следовательно, (dn/dy) = (∂n/∂r) (∂r/∂y) = (∂n/∂r) (y/r) ≈ (∂n/∂r) (l/r). Внутри сердцевины волокна наблюдается слабое отличие у от l. Угол наклона луча с учетом (1) выражается интегральным соотношением
![]() (2)
(2)
Вертикальная координата y луча в плоскости изображения (рис. 1)
![]() . (3)
. (3)
Из (2) и (3) интегральное уравнение для искомой функции n(r), т. е. радиального распределения показателя преломления, имеет вид:
![]() (4)
(4)
Если функция [у(l)–l] известна, то распределение показателя преломления является решением интегрального уравнения (4). С введением обозначений
![]() (5)
(5)
интегральное уравнение принимает вид:
![]() (6)
(6)
Здесь верхний предел интеграла ∞, поскольку G(r) = 0 для r>а. Функция G (r) имеет вид:
![]() , (7)
, (7)
тогда
![]() , (8)
, (8)
где: J0 — функция Бесселя нулевого порядка.
Уравнение (8) является преобразованием Ханкеля известного обратного интегрального преобразования:
![]() . (9)
. (9)
Подставляя (9) в (7), можно получить развернутое интегральное представление G (r) через F(l):
![]() .
.
При интегрировании по ![]() окончательно получается
окончательно получается
![]() ; (10)
; (10)
![]() . (11)
. (11)
Входящая в основное интегральное уравнение (11) функция у(l) определяется путем прямого интегрирования плотности потока излучения Р(l). Действительно, из закона сохранения энергии в потоке излучения следует, что мощность Р(y)dy, переносимая через элемент длины dy, не зависит от координаты x. Поэтому P(l)dl=P(y)dy, где ![]() — плотность потока на входе в ОВ, а
— плотность потока на входе в ОВ, а ![]() — в плоскости изображения. При нормировании плотности потока излучения таким образом, чтобы
— в плоскости изображения. При нормировании плотности потока излучения таким образом, чтобы ![]() , получается дифференциальное выражение dl=P(y)dy, после интегрирования которого
, получается дифференциальное выражение dl=P(y)dy, после интегрирования которого
![]() (12)
(12)
определяется обратная функция. Из нее находится и требуемая у(l), т. е. прямая функция, входящая в уравнение (11). При измерениях плоскость изображения определяется предметной плоскостью, на которую сфокусирован микроскоп.
Уравнение (11) справедливо, если объектив микроскопа, наведенный на плоскость изображения, согласован с показателем преломления путем погружения в иммерсионную жидкость. При отсутствии иммерсионной жидкости, т. е. когда объектив граничит с воздухом, необходимо учесть отражение и преломление света на границе жидкость — воздух. При этом (11) преобразуется к виду
![]() (13)
(13)
Плоскость изображения необходимо удалить от оси сердцевины на расстояние до точки пересечения рефрагировавших лучей, покинувших ее. Наличие пересечения лучей нарушает однозначное соответствие между у и l, выражаемое соотношением (12). Оптимальным является расположение плоскости изображения непосредственно за сердцевиной, где L = a. При этом точка пересечения лучей, получаемая при продолжении входного и выходного направлений луча в сердцевину, расположена вблизи x = 0 (рис. 1).
Интеграл (13), по которому рассчитывается распределение показателя преломления n (r), несколько напоминает аналогичный интеграл, получаемый с помощью метода интерферометрии при поперечном освещении. Однако между ними имеются два существенных различия. Во-первых, в случае фокусировки первичную информацию (плотность потока излучения P(y)) в соответствии с (12) интегрируют, а не дифференцируют, что является значительным преимуществом, поскольку интегрирование приводит к сглаживанию случайных флуктуаций, вызванных шумами приборов, в то время как дифференцирование вызывает усиление сигнала с шумами. Во-вторых, хотя подынтегральное выражений в (11) имеет полюс при l=r, его вклад в ошибку не стремится к бесконечности в точке r = 0, поскольку l – y (l) также обращается в нуль в этой точке. Погрешность метода фокусировки максимальна на оси волокна, но остается конечной.
Вклад в результирующую погрешность вносит также допущение, что y = l.
Отклонение луча внутри сердцевины определяется с учетом параболического распределения показателя преломления ![]() ,где n0 — показатель преломления на оси;
,где n0 — показатель преломления на оси; ![]() — параметр профиля. Решение уравнения параксиального луча имеет вид
— параметр профиля. Решение уравнения параксиального луча имеет вид ![]() .
.
Координата z параллельна координате х (рис.1), но её начало сдвинуто таким образом, что в точке, где луч входит в сердцевину, z= 0. В точке выхода ![]() максимальное отклонение
максимальное отклонение
![]() .
.
Отсюда максимальное смещение луча в сердцевине ![]() .
.
Среднее смещение луча по траектории внутри сердцевины ![]() .
.
У стандартных волокон Δ = 0,01 и смещение луча мало. Распределение плотности потока в стандартном волокне показано на рис. 2 сплошной кривой. На рис. 3.а сплошной линией изображен профиль показателя преломления ОВ, а штриховой — профиль того же волокна, определяемый методом интерферометрии среза, откуда видно, что центральный провал плохо разрешен методом фокусировки, если плоскость изображения выбрана на расстоянии
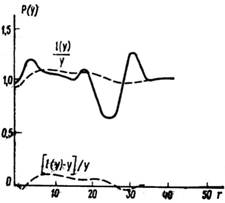
Рискнок 2. Распределение плотности потока в стандартном волокне
L=a. Снижение разрешающей способности вызвано тем, что центральный провал представляет собой сильную линзу диаметром несколько микрометров и лучи, проходящие через нее, пересекаются еще до того, как достигнут плоскости изображения. На рис. 3.б сплошной линий показан профиль, также определяемый методом фокусировки, плоскость изображения которого находилась в этом случае на расстоянии L= 16 мкм от оси волокна с радиусом сердцевины а =28 мкм. Наблюдаемый центральный провал углубляется при смещении плоскости изображения внутрь сердцевины. Как видно из рис. 3.б, размещение плоскости изображения в непосредственной близости от локализованных областей позволяет повысить, разрешение резко локализованных областей волокна со значительными градиентами показателя преломления (штриховой линией для сравнения показан профиль, полученный интерференционным методом). Однако повышение разрешающей способности в малых областях дается ценой потери информации о других областях.
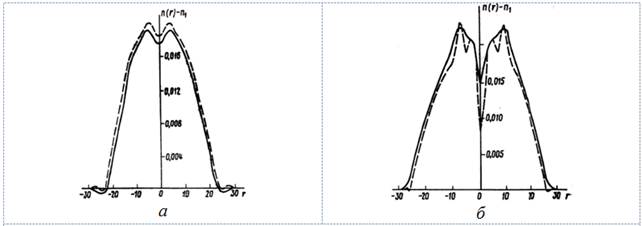
Рисунок 3. Профили показателя преломления, измеренные методами фокусировки и интерферометрии среза
При вытягивании волокна из заготовки форма профиля показателя преломления сохраняется, трансформируется только радиальный размер, что обеспечивает достоверное представление о распределении показателя преломления волокна. Необходимо учитывать, что на измеренном с достаточно высокой точностью профиле показателя преломления заготовок видна микроструктура отдельных слоев сердцевины, в то время как в волокне эта структура размыта, поскольку ее характерные размеры соизмеримы с длиной волны зондирующего излучения.
Определение абсолютной точности метода измерения всегда является сложной задачей из-за наличия многих скрытых источников погрешностей. Однако уравнения (12) и (13) позволяют установить погрешность случайных и систематических флуктуаций уровня плотности потока излучения Р(у). Определив
![]() , (14)
, (14)
можно записать, что Δn0 — решение уравнения (14) при отсутствии погрешности. Кроме того, ![]() , где y0 — значение при отсутствии погрешности. Из (13) для усредненного значения (определяемого скобками
, где y0 — значение при отсутствии погрешности. Из (13) для усредненного значения (определяемого скобками ![]() ) можно получить
) можно получить
![]() .
.
С использованием соотношения dy/dl= 1/P, которое следует из (12), с помощью дифференцирования можно записать
![]() , (15)
, (15)
где: P0 — идеальное значение. Из (15) можно получить
![]() .
.
Функция корреляции для быстрых случайных флуктуаций плотности
![]() , (16)
, (16)
где: σ — длина корреляции (малая величина). Используя (16), можно переписать (12) в виде
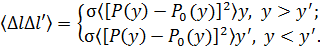 .
.
Из рис. 2 видно, что Р(у) колеблется вокруг значений единицы, а у(l) — значения l. Поэтому приближенно можно считать Р0(у) = 1 и у = l. Тогда порядок погрешности показателя преломления
![]() .
.
Уравнение определяет погрешность профиля, вызванную быстрыми случайными пространственными флуктуациями плотности потока излучения. Однако помимо случайных флуктуаций с очень малой длиной корреляций необходимо рассмотреть изменение Р(у) во времени. Поскольку облучение по полю наблюдения микроскопом не обязательно постоянно, необходимо замерить распределение интенсивности в отсутствие волокна и использовать эти уравнения для калибровки измеренной интенсивности излучения в присутствии сердцевины волокна. Любые флуктуации источника излучения в течение времени между калибровкой и измерениями будут искажать результаты определения профиля показателя преломления.
Длительные флуктуации излучения рассматриваются как систематическая погрешность δР плотности. Поскольку у(l) определяется по Р(у) из (12), он также вносит систематическую погрешность δу. Погрешность показателя преломления может быть получена из выражения (13):
![]() .
.
Используя (15), можно переписать (12) в виде
![]() ,
,
и получить δу = у[(δР)/Р0]. Грубая оценка получается при использовании приближения Р0=1 и у=l. Интегрирование приводит к δ(Δn)=[(n1)/(πL)](а2—r2)1/2 δP. Флуктуации повторных замеров показателя преломления при отсутствии усреднения δ(Δn)=0,003, а в случае усреднения по 100 замерам интенсивности излучения δ(Δn)=0,0005. Эту погрешность можно полностью отнести за счет временных флуктуаций излучения при δР=0,7 % без усреднения и δР=0,1 % с усреднением.
Описанный метод фокусировки справедлив только для объектов, помещенных в иммерсионную жидкость. Вместо иммерсионной жидкости так же можно ввести цилиндрические согласующие линзы. Эта модификация метода фокусировки используется для контроля заготовок одномодовых волокон, но не применима для многомодовых, что обусловлено двумя факторами:
1. световой пучок внутри заготовки не может быть сколлимирован, что ограничивает область ввода излучения;
2. аберрации согласующих линз уменьшают внутри заготовки область, в которой коллимация пучка может быть достигнута оптическими методами.
На практике только половина центральной области поперечного сечения заготовки применима для метода фокусировки с использованием согласующих линз вместо иммерсионной жидкости. Преимуществом подобной модификации является устранение возможности разрушения поверхностей заготовки в процессе очистки при удалении остатков иммерсионной жидкости, что приводит к снижению прочности волокна. Кроме того, эта методика позволяет получить информацию о специальных заготовках с высокими показателями преломления или большими длинами волн облучения, для которых невозможно подобрать подходящую иммерсионную жидкость.
Список литературы:
1.Андросик А.Б., Воробьев С.А., Мировицкая С.Д. Рефракционный метод исследования волоконных световодов. Lambert Acamic Publishing 2012 — 183 с.
2.Лазарев Л.П., Мировицкая С.Д. Исследование оптических схем реализации измерителей геометрических характеристик оптических волокон и капилляров. ЦНИИТЭИ приборостр., Измерения, контроль, автоматизация — 1986, — № 3, — с. 52—86.
дипломов


Оставить комментарий