Статья опубликована в рамках: XXVII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 30 октября 2013 г.)
Наука: Технические науки
Секция: Машиностроение и машиноведение
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ СКОЛЬЗЯЩЕГО УДАРА ЭЛЕМЕНТОВ МЕХАНИЗМА СВОБОДНОГО ХОДА (МСХ) БЛОЧНОЙ КОНСТРУКЦИИ
Шенкман Людмила Владиславовна
канд. техн. наук., доцент ФГБОУВПОКГТА им. В.А. Дегтярева, г. Ковров
E-mail: lusishenk@mail.ru
Козлова Светлана Николаевна
канд. техн. наук, доцент ФГБОУВПОКГТА им. В.А. Дегтярева, г. Ковров
Савина Елена Сергеевна
студент ФГБОУВПОКГТА им. В.А. Дегтярева, г. Ковров
MATHEMATICALMODEL OF THE ROLLING IMPACT ELEMENTS OF FREERUNNING (MCX) BLOCK DESIGN
Shenkman Luidmila
candidate of Technical Sciences, Associate Professor of Federal state budgetary educational institution higher professional education Kovrov state technological academy named after V.A. Degtayrev
Kozlova Svetlana
candidate of Technical Sciences, Associate Professor of Federal state budgetary educational institution higher professional education Kovrov state technological academy named after V.A. Degtayrev
Savina Elena
student of Federal state budgetary educational institution higher professional education Kovrov state technological academy named after V.A. Degtayrev
АННОТАЦИЯ
Оригинальный блочный механизм свободного хода (МСХ) отличается высокой прочностью зуба при малом шаге. Однако, работа храповых МСХ сопровождается ударами, которые приводят к поломкам. Предлагаемая математическая модель поможет спроектировать МСХ с оптимальными размерами и снизить ударные нагрузки.
ABSTRACT
Original block overrunning clutch is highlydurable tooth with a small step. However, the work of the ratchet — gear free — wheel clutch mechanisms of agricultureis accompanied by blows that lead to breakdowns. The proposed mathematical model will help design the free-wheel clutch mechanism with optimal size and reduce shock loads.
Ключевые слова: храповой МСХ; скользящий удар; математическая модель.
Keywords: ratchet MCX; sliding kick; mathematicalmodel.
В импульсных механизмах МСХ испытывают большие динамические нагрузки, и все известные конструкции быстро выходят из строя. Блочный МСХ — оригинальная конструкция храпового МСХ. Эксперименты показали его более высокую, по сравнению с другими известными конструкциями, надежность.
Чтобы на стадии проектирования снизить ударные нагрузки, и подобрать оптимальные конструктивные параметры храпового МСХ блочного типа, разработана, в частности, математическая модель скользящего удара элементов МСХ.
Предлагаемое решение является развитием метода расчета чисто упругого контактного удара [3, с. 37] с учетом распространения его на случаи, когда в зоне контакта возникает скольжение.
Суть рассматриваемого процесса приведена на рис. 1, б. Происходит скользящий периодический удар и отскок собачки при невключенном МСХ. Уравнение движения в период соударения собачки и храповика:
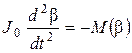 , (1)
, (1)
где: J0 — приведенный момент инерции соударяющихся тел;
М(β) — текущее значение момента соударения, изменяющееся от 0 до М(β)max.
На рис. 1 приведены фрагменты взаимодействия собачки и зуба храповика при соударении, где α(β) — величина местной деформации, β(α) — угол поворота собачки, соответствующий этой деформации. На рис. 1, а — торцевой удар при замыкании МСХ, на рис. 1, б — скользящий удар собачки при соскоке в режиме холостого хода.
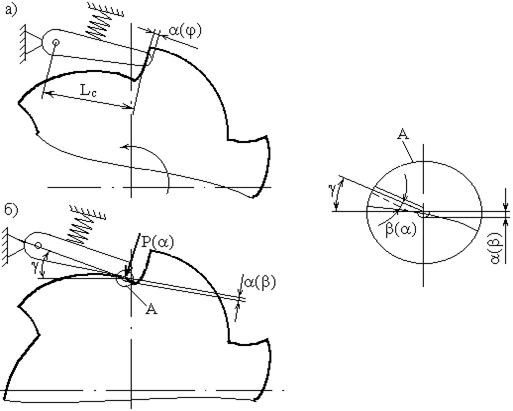
Рисунок 1. Фрагменты взаимодействия собачки и зуба храповика
Для случая скользящего удара приведенный момент инерции:
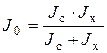 ,
,
где: Jc — момент инерции собачки относительно оси вращения;
Jx — момент инерции вращающейся части храповика.
Момент инерции собачки значительно меньше момента инерции храповика Jс<< Jкр, следовательно:
J0 ≈ Jс (2)
Учитывая соотношение (2), окончательно уравнение (1) примет вид:
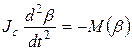 , (3)
, (3)
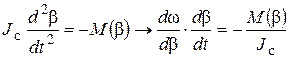 ,
,
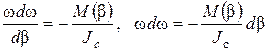 ,
,
 , (4)
, (4)
при t = 0, ω = ω0,  .
.
Подставляя значение постоянной С в уравнение (4), получаем:
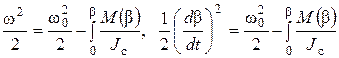 ,
,
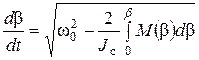 . (5)
. (5)
Преобразовывая уравнение (5) методом разделения переменных продолжительность активной части деформации можно определить из выражения:
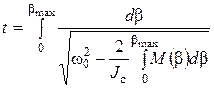 . (6)
. (6)
Время t рассматривается с момента первого касания собачки поверхности зуба до достижения максимальной местной деформации. Для решения уравнения (6) используется формула Герца:
![]() ,
,
где: b — коэффициент, зависящий от геометрических параметров контактирующих поверхностей и материалов тел;
α — сближение соударяющихся тел в зоне контакта.
Для рассматриваемого случая ни одно из условий, при которых справедлива формула Герца, не соблюдается. В частности:
· вектор скорости соударения не перпендикулярен к поверхности контакта;
· в зоне контакта имеет место пластическая деформация;
· между телами в момент соударения имеет место скольжение.
В связи с отмеченными отклонениями для решения процесса соударения используется видоизмененная формула Герца [2, с. 82]:
![]() , (7)
, (7)
где: n — показатель степени, отличный от 3/2 при чисто упругом ударе;
b — коэффициент, зависящий от геометрии контактирующий поверхностей при наличии пластической деформации.
Из геометрических соотношений (рис. 1, б) и с учетом (7):
![]() ,
,
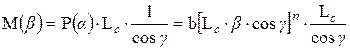 ,
,
![]()
 . (8)
. (8)
В момент наибольшего сближения ![]()
Из выражения (5):
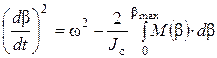 ,
,
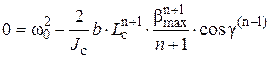 . (9)
. (9)
Наибольший угол β при ударе:
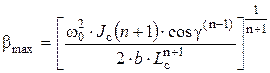 . (10)
. (10)
Для определения времени активного соударения из выражения (5), вводя обозначения А2=![]() и
и ![]() , можно получить выражение:
, можно получить выражение:
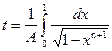 . (11)
. (11)
Выражение (11) решается с помощью Гамма-функции, в частности [1, ср. 44]:
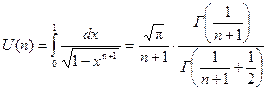 .
.
С учетом значения функции U(n) время активной части соударения определяется из:
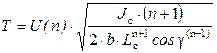 .
.
Из выражения (6) с учетом (8), (9) и (11):
![]() ,
,
![]()
 (12)
(12)
Наибольшее усилие при ударе:
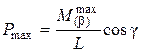 . (13)
. (13)
С учетом выражений (8) и (13):
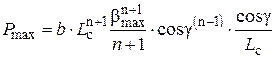 ,
,
![]() ,
,
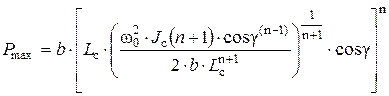 ,
,
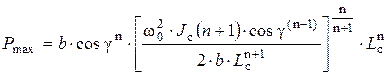
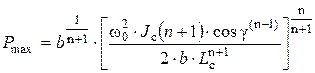 (14)
(14)
Полученные уравнения (12) и (14) позволяют описать математический процесс движения собачки при вращении храповика в режиме холостого хода, с учетом имеющей место упругопластической деформации в зоне контакта собачки и зуба храповика. Используя параметры пластической твердости НД, позволяющие оценить коэффициенты в уравнении (7) получаем следующие эмпирические зависимости:
![]() ,
,
![]() ,
,
где: Dпр — приведенный диаметр поверхности соударения;
НД — показатель пластической твердости, учитывающий термическую обработку материала.
Полученные эмпирические зависимости справедливы при оценке НД методом шарового индентора. Для цилиндрического индентора при одинаковом радиусе с шаровым сравнительные показания соотносятся как
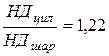
Список литературы:
1.Бронштейн И.Н., Семендяев К.А. Справочник по высшей математике. М.: Наука, 1980 г.
2.Дрозд М.С., Матлин М.М., Сидякин Ю.И. Инженерные расчеты упруго-пластической деформации. М.: Машиностроение, 1986. — 230 с.
3.Ионов В.Н., Огибалов П.М. Напряжения в телах при импульсном нагружении. М.: Высшая школа, 1975.
дипломов


Оставить комментарий