Статья опубликована в рамках: XXVI Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 02 октября 2013 г.)
Наука: Технические науки
Секция: Строительство и архитектура
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ФОРМИРОВАНИЕ ОСНОВНОГО МАТРИЧНОГО УРАВНЕНИЯ МЕТОДА ГРАНИЧНЫХ ЭЛЕМЕНТОВ ДЛЯ РАСЧЕТА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ НАДЗЕМНОГО МАГИСТРАЛЬНОГО НЕФТЕПРОВОДА
Смирнов Владимир Викторович
ассистент кафедры транспорта углеводородных ресурсов Тюменского государственного нефтегазового университета, г. Тюмень.
E-mail: smirnovvladimir@mail.ru
Земенков Юрий Дмитриевич
д-р техн. наук, проф., заведующий кафедрой транспорта углеводородных ресурсов Тюменского государственного нефтегазового университета, г. Тюмень.
FORMATION OF THE BASIC MATRIX EQUATIONS BY BOUNDARY ELEMENT TECHNIQUE FOR CALCULATION OF THE STRAINED-DEFORMATED STATE OF ABOVE-GROUND MAIN OIL PIPELINES
Vladimir Smirnov
assistant of the Department of Transport of hydrocarbon resources of the Tyumen State Oil and Gas University, Tyumen
Yuri Zemenkov
doctor of Technical Sciences, professor, head of the transport of hydrocarbon resources of the Tyumen State Oil and Gas University, Tyumen
АННОТАЦИЯ
В статье рассматривается процесс формирования основного матричного уравнения метода граничных элементов, заполнение входящих в него векторов и матриц, для решения задачи расчета напряженно-деформированного состояния надземного участка магистрального нефтепровода с компенсатором, в балочном приближении.
ABSTRACT
The article presents the process of forming the basic matrix equation of the boundary element technique, the filling of vectors and matrix to solve the task of strained-deformated state for above-ground section of the main oil pipeline with a compensator, in bar approximation.
Ключевые слова: магистральный нефтепровод; метод граничных элементов; матрица; напряженно-деформированное состояние.
Keywords: main oil pipeline; boundary element technique; matrix; strained-deformated state.
Расчет напряженно-деформированного состояния магистральных нефтепроводов в настоящее время базируется на трех основных моделях: балочная модель, оболочечная модель, объемная модель [4] В работах [3, 4] отмечается, что решение задачи в балочной модели есть первое приближение к получению картины НДС для протяженного объекта, необходимой для дальнейших исследований. Для решения этой задачи, как правило, применяются численные методы, действующие в основе современных программ, среди них наиболее часто используется метод конечных элементов [8].
При рассмотрении надземных трубопроводов как протяженной конструкции в балочном приближении, актуальной альтернативой МКЭ является метод граничных элементов (МГЭ). Это объясняется тем, что изменения внешней нагрузки происходят только в местах крепления трубопровода к опорам, рассматриваемые как (границы стержней), в отличие от подземного трубопровода, который может иметь контакт с окружающим грунтом практически на всем протяжении трассы. Методика применения МГЭ к задачам строительной механики приведена в работах [1, 2]. Авторы этих работ доказывают преимущества метода МГЭ перед МКЭ для задач поперечного изгиба, которые являются значимой частью задач расчета НДС балочных конструкций. В частности автор указывает на сокращение количества ненулевых элементов матрицы МГЭ до 10 по сравнению с 16 в аналогичной матрице МКЭ. Также в работе [2] приводятся решения задач для различных простых балочных систем и продемонстрирована многочисленная сверка результатов с другими авторами, решавшими аналогичные задачи иными методами, что является подтверждением достоверности результатов получаемых при применении предлагаемых уравнений.
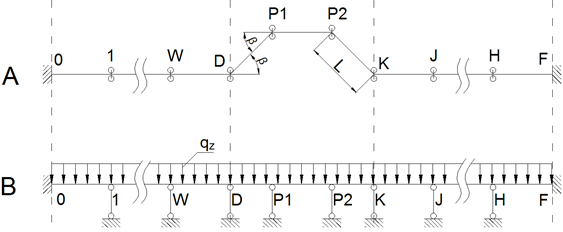
Рисунок 1. Расчетная схема надземного участка магистрального нефтепровода с П-образным компенсатором. А — вид сверху. Б — вид с боку
Рассмотрим процесс формирования основных матричных уравнений по методике, предложенной в [2] для решения задачи расчета надземного участка магистрального нефтепровода с П-образным компенсатором (см. рис. 1). Схема рассматривалась в работе [6], в рамках разрабатываемого алгоритма расчета надземных трубопроводов, являющегося составной частью методики контроля НДС надземных трубопроводов предложенной в статье [5]. В качестве элемента рассматривается пролет между опорами. На схеме опоры 0 и F — неподвижные; 1, W, J, H — продольно-подвижные; D, P1, P2, K — свободно-подвижные. Основное матричное уравнение имеет вид (1)
, (1)
Векторы Y(L) и X(0) являются векторами значений параметров НДС стержней в граничных точках. Сущность преобразования 
в 
(1) заключается в переносе ненулевых параметров Y(L) на место нулевых параметров X(0) при этом появляются компенсирующие элементы, обеспечивающие неизменность уравнения относительно первоначального. Кроме этого устанавливаются уравнения связи между зависимыми параметрами , коэффициенты при зависимых параметрах также становятся компенсирующими элементами матрицы C. Матрица A*(L) является результатом сложения матриц A(0)+C, где A(0) — матрица A(L) с обнуленными столбцами номера которых являются номерами нулевых элементов X(0), матрица С имеет масштаб матрицы A и заполнена компенсирующими элементами, образующимися при преобразовании в . Решение уравнения (1) позволяет получить начальные и конечные граничные параметры, на основании которых решаются известные уравнения строительной механики с зависимостью по продольной координате для поперечного изгиба в вертикальной и горизонтальной плоскости, кручения и растяжения сжатия. Перечисленные уравнения позволяют учесть необходимые нагрузки в соответствии с требованиями [7].
Для однозначного понимания дальнейшего изложения следует привести список принятых обозначений (см. табл. 1). В таблице 2 приведены данные о наличии нулевых и не нулевых элементов векторов X(0) и Y(L) для схемы на рисунке 1. Результат переноса параметров — итоговый вектор неизвестных значений X(0,L) представлен в таблице 3.
Таблица 1.
Список принятых обозначений
|
vy |
Поперечное перемещение в горизонтальной плоскости |
||||
|
vz |
Поперечное перемещение в вертикальной плоскости |
||||
|
fy |
Угол поперечного изгиба в горизонтальной плоскости |
||||
|
fz |
Угол поперечного изгиба в вертикальной плоскости |
||||
|
My |
Изгибающий момент в горизонтальной плоскости |
||||
|
Mz |
Изгибающий момент в вертикальной плоскости |
||||
|
Qy |
Поперечная сила в горизонтальной плоскости |
||||
|
Qz |
Поперечная сила в вертикальной плоскости |
||||
|
Nk |
Продольные усилия, создаваемые кольцевым напряжением вследствие действия внутреннего давления |
||||
|
dt |
Разница температур в момент закрепления участка и технологической температуры |
||||
|
α |
коэффициент температурного расширения материала трубопровода |
||||
|
qy |
Распределенная нагрузка в горизонтальной плоскости |
||||
|
qz |
Распределенная нагрузка в вертикальной плоскости |
||||
|
A |
Площадь сечения трубопровода (стенки) |
||||
|
G |
Модуль сдвига |
Mk |
Крутящий момент |
N |
Продольное усилие |
|
E |
Модуль упругости |
Θ |
Угол закручивания |
u |
Продольное перемещение |
|
I |
Осевой момент инерции |
Ik |
Полярный момент инерции |
L |
Длина пролета трубопровода |
Таблица 2.
Нулевые и ненулевые значения элементов векторов начальных X(0) и конечных Y(L) граничных параметров
|
|
Вектор X(0) |
Вектор Y(L) |
||||||||||||||||
|
№ элем. (сверху вниз) |
1- 12 |
13 -24 |
25- 36 |
37- 48 |
49- 60 |
61- 72 |
73- 84 |
85- 96 |
97- 108 |
1- 12 |
13- 24 |
25- 36 |
37- 48 |
49- 60 |
61- 72 |
73- 84 |
85- 96 |
97- 108 |
|
Пара метр |
0 -1 |
1- W |
W- D |
D -P1 |
P1 -P2 |
P2 -K |
K- J |
J- H |
H -F |
0- 1 |
1- W |
W- D |
D- P1 |
P1- P2 |
P2- K |
K- J |
J- H |
H- F |
|
EIvy |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
EIfy |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
My |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Qy |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
EIvz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
EIfz |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
Mz |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Qz |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
GIkΘ |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
Mk |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
EAu |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
N |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Таблица 3.
Вектор неизвестных значений X(0,L)
|
1-12 |
13-24 |
25-36 |
37-48 |
49-60 |
61-72 |
73-84 |
85-96 |
97-108 |
|
MyH-F(L) |
Qy1-W(L) |
MkH-F(L) |
EIvyD-P1(0) |
EIvyP1-P2(0) |
EIvyP2-K(0) |
EIvyK-J(0) |
QyJ-H(L) |
QyH-F(L) |
|
MzH-F(L) |
EIfy1-W(0) |
EIfyW-D(0) |
EIfyD-P1(0) |
EIfyP1-P2(0) |
EIfyP2-K(0) |
EIfyK-J(0) |
EIfyJ-H(0) |
EIfyH-F(0) |
|
My0-1(0) |
My1-W(0) |
MyW-D(0) |
MyD-P1(0) |
MyP1-P2(0) |
MyP2-K(0) |
MyK-J(0) |
MyJ-H(0) |
MyH-F(0) |
|
Qy0-1(0) |
Qy1-W(0) |
QyW-D(0) |
QyD-P1(0) |
QyP1-P2(0) |
QyP2-K(0) |
QyK-J(0) |
QyJ-H(0) |
QyH-F(0) |
|
NH-F(L) |
Qz1-W(L) |
QzW-D(L) |
QzD-P1(L) |
QzP1-P2(L) |
QzP2-K(L) |
QzK-J(L) |
QzJ-H(L) |
QzH-F(L) |
|
Qy0-1(L) |
EIfz1-W(0) |
EIfzW-D(0) |
EIfzD-P1(0) |
EIfzP1-P2(0) |
EIfzP2-K(0) |
EIfzK-J(0) |
EIfzJ-H(0) |
EIfzH-F(0) |
|
Mz0-1(0) |
Mz1-W(0) |
MzW-D(0) |
MzD-P1(0) |
MzP1-P2(0) |
MzP2-K(0) |
MzK-J(0) |
MzJ-H(0) |
MzH-F(0) |
|
Qz0-1(0) |
Qz1-W(0) |
QzW-D(0) |
QzD-P1(0) |
QzP1-P2(0) |
QzP2-K(0) |
QzK-J(0) |
QzJ-H(0) |
QzH-F(0) |
|
Qz0-1(L) |
GIkO1-W(0) |
GIkOW-D(0) |
GIkOD-P1(0) |
GIkOP1-P2(0) |
GIkOP2-K(0) |
GIkOK-J(0) |
GIkOJ-H(0) |
GIkOH-F(0) |
|
Mk0-1(0) |
Mk1-W(0) |
MkW-D(0) |
MkD-P1(0) |
MkP1-P2(0) |
MkP2-K(0) |
MkK-J(0) |
MkJ-H(0) |
MkH-F(0) |
|
QyK-J(L) |
EAu1-W(0) |
EAuW-D(0) |
EAuD-P1(0) |
EAuP1-P2(0) |
EAuP2-K(0) |
EAuK-J(0) |
EAuJ-H(0) |
EAuH-F(0) |
|
N0-1(0) |
N1-W(0) |
NW-D(0) |
ND-P1(0) |
NP1-P2(0) |
NP2-K(0) |
NK-J(0) |
NJ-H(0) |
NH-F(0) |
Уравнения связи между конечными и начальными граничными параметрами в основном представляют равенство конечного и начального значений (в случае их существования: наличие символа 1 в таблице 2). При этом в матрицу С заносится компенсирующий элемент равный –1 (коэффициент при равенстве значений параметров равен 1, однако необходимо учесть знак перед вектором Y(L)), в ячейку номер строки которой равен номеру строки в векторе Y(L), а номер столбца равен номеру строки в векторе X(0).Перенос независимых параметров также сопровождается внесением компенсирующего элемента, по тому же принципу. Наиболее сложными являются уравнения, составленные для области компенсатора, т. е. пролетов W-D, D-P1, P1-P2, P2-K, рассмотрим их на примере W-D представленном в таблице 4. Из представленного примера видно, что уравнения связи определяются геометрической формой участка и опорных условий.
Таблица 4.
Уравнения связи между конечными граничными параметрами W-D и начальными параметрами D-P1
|
№ |
Y(L) |
|
Компенсирующий элемент |
X(0) |
№ |
|
Компенсирующий элемент |
X(0) |
№ |
|
25 |
EIvyW-D(L) |
= |
-cosb |
EIvyD-P1(0) |
37 |
+ |
-I/A*sinb |
EAuD-P1(0) |
47 |
|
26 |
EIfyW-D(L) |
-1 |
EIfyD-P1(0) |
38 |
|
|
|
||
|
27 |
MyW-D(L) |
-1 |
MyD-P1(0) |
39 |
|
|
|
||
|
28 |
QyW-D(L) |
-cosb |
QyD-P1(0) |
40 |
sinb |
ND-P1(0) |
48 |
||
|
29 |
EIvzW-D(L)=0 |
|
|
|
|
|
|
||
|
30 |
EIfzW-D(L) |
-1 |
EIfzD-P1(0) |
42 |
|
|
|
||
|
31 |
MzW-D(L) |
-sinb |
MkD-P1(0) |
46 |
-cosb |
MzD-P1(0) |
43 |
||
|
32 |
QzW-D(L) |
|
|
|
|
|
|
||
|
33 |
GIkOW-D(L) |
-1 |
GIkOD-P1(0) |
45 |
|
|
|
||
|
34 |
MkW-D(L) |
sinb |
MzD-P1(0) |
43 |
-cosb |
MkD-P1(0) |
46 |
||
|
35 |
EAuW-D(L) |
a/I*sinb |
EAvyD-P1(0) |
37 |
-cosb |
EAuD-P1(0) |
47 |
||
|
36 |
NW-D(L) |
-cosb |
ND-P1(0) |
48 |
-sinb |
QyD-P1(0) |
40 |
Для учета нагрузки используется вектор B(L), в котором для случая надземного магистрального нефтепровода следует учитывать вертикальную совокупную нагрузку в вертикальной плоскости: собственный вес трубопровода, вес продукта, снеговая и гололедная нагрузка, — также ветровую нагрузку в горизонтальной плоскости, продольное расширение под воздействием внутреннего давления и температуры, а также силу трения на опорах, которая должна быть учтена для продольно подвижных и свободноподвижных опор.
Таблица 5.
Вектор нагрузки B(L)
|
|
|
0-1, 1-W, W-D, P1-P2, K-J, J-H, H-F |
D-P1, P2-K |
|
EIvy |
B1 |
qy*L^4/24 |
qy*L^4/24*cos(b) |
|
EIfy |
B2 |
qy*L^3/6 |
qy*L^3/6*cos(b) |
|
My |
B3 |
qy*L^2/2 |
qy*L^2/2*cos(b) |
|
Qy |
B4 |
qy*L |
qy*L*cos(b) |
|
EIvz |
B5 |
-qz*L^4/24 |
-qz*L^4/24 |
|
EIfz |
B6 |
-qz*L^3/6 |
-qz*L^3/6 |
|
Mz |
B7 |
-qz*L^2/2 |
-qz*L^2/2 |
|
Qz |
B8 |
-qz*L |
-qz*L |
|
GIkO |
B9 |
0 |
0 |
|
Mk |
B10 |
0 |
0 |
|
EAu |
B11 |
E*A*L*α*dt+L*Nk*a |
E*A*L*α*dt+L*Nk*A |
|
N |
B12 |
0 |
0 |
В таблице 5 приведен вектор B(L) для данного примера без учета сил трения, так как этот вид нагрузки требует отдельного обоснования при вводе. Суммарная вертикальная и горизонтальная нагрузки рассматриваются как распределенные, учет продольных расширений под воздействием внутреннего давления и температуры вводится как конечное значение перемещения.
Таким образом, применимость метода граничных элементов к решению задач напряженно-деформированного состояния магистральных нефтепроводов вполне возможна и является относительно несложной. По полученным значениям граничных параметров на основании известных уравнений строительной механики можно построить линию деформированного состояния трубопровода, и при учете напряжений создаваемых внутренним давлением получить картину распределения напряжений на протяженных участках трубопровода.
Список литературы:
1.Баженов В.А. Строительна механика. Специальный курс. Применение метода граничных элементов / В.А. Баженов, В.Ф. Оробей, А.Ф. Дащенко, Л.В. Коломиец // Одесса: Астропринт. 2001. — 284 с.
2.Баженов В.А. Численные методы в механике / Баженов В.А. [и др.] Одесса: Драфт. 2005. — 564 с.
3.Ефимов А.И. Исследование НДС и оценка прочности трубопроводных систем: дис. канд. техн. наук : 01.02.06 / ПГТУ. Пермь. 2010. — 120 с.
4.Рудаченко А.В., Саруев А.Л. Исследования напряженно-деформированного состояния трубопроводов. Томск: Изд-во ТПУ. 2011. — 136 с.
5.Смирнов В.В. Повышение надежности эксплуатации надземных магистральных нефтепроводов на многолетнемерзлых грунтах / Смирнов В.В., Земенков Ю.Д.//. Нефть и газ: Отдельный выпуск Горного информационно-аналитического бюллетеня (научно-технического журнала). М.: Издательство «Горная книга». — 2013. — № ОВ3. — С. 197—208.
6.Смирнов В.В. Применение метода граничных элементов для расчета напряженно-деформированного состояния надземных магистральных нефтепроводов, проложенных на многолетнемерзлых грунтах / Смирнов В.В., Земенков Ю.Д.. // Трубопроводный транспорт: теория и практика. — 2013. — № 4. — С. 18—23.
7.СНиП 2.05.06-85. Магистральные нефтепроводы. Введ.1986-01-01. С изм.1987,1990,1996 гг. М.: ВНИИСТМиннефтегазстроя, 1997. — 64 с.
8.Яваров А.В. Напряженно-деформированное состояние подземных трубопроводов / А.В. Яваров, Г.С. Колосова, В.В. Куроедов //. Интернет-журнал «Строительство уникальных зданий и сооружений». — 2013. — № 1. — С. 1—10. [Электронный ресурс] — Режим доступа. — URL: http://www.unistroy.spb.ru/. Дата обращения: 6.09.2013.
дипломов
Оставить комментарий