К  ВОПРОСУ  О  СТРУКТУРЕ  УСТОЙЧИВЫХ  И  НЕУСТОЙЧИВЫХ  РЕШЕНИЙ  ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНОГО  УРАВНЕНИЯ

Красильников  Александр  Яковлевич

д-р  техн.  наук,  профессор,  ФГАОУ  ВПО  «Уральский  федеральный  университет  им.  первого  Президента  России  Б.Н.  Ельцина»,  Екатеринбург

E-mail:  Krasilnikov1951@yandex.ru

Кравченко  Константин  Юрьевич

аспирант,  ФГАОУ  ВПО  «Уральский  федеральный  университет  им.  первого  Президента  России  Б.Н.  Ельцина»,  Екатеринбург

E-mail:  laPosteGenerale@gmail.com

ON  THE  STRUCTURE  OF  STABILITY  AND  INSTABILITY  SOLUTIONS  OF  DELEY-DIFFERENTIAL  EQUATION

Alexsandr  Krasilnikov

doctor  of  engineering  science,  professor,  Ural  Federal  University  named  after  the  first  President  of  Russia  B.N.  Yeltsin,  Ekaterinburg

Konstantin  Kravchenko

postgraduate,  Ural  Federal  University  named  after  the  first  President  of  Russia  B.N.  Yeltsin,  Ekaterinburg

АННОТАЦИЯ

Рассматривается  математическая  модель  с  одной  степенью  свободы,  описывающая  процесс  резания  материала,  и  соответствующее  скалярное  дифференциально-разностное  уравнение  второго  порядка.  Решается  задача  о  построении  границы  устойчивости  исходного  уравнения.  Исследуется  поведение  решений  уравнения  на  границе  устойчивости.  Сделаны  замечания  о  поведении  решений  дифференциально-разностного  уравнения  вблизи  границы  устойчивости. 

ABSTRACT

Single  degree  of  freedom  model  of  cutting  process  and  corresponding  second-order  delay  differential  equation  of  the  system  are  under  consideration.  Stability  analysis  of  presented  model  is  suggested.  In  present  paper  behavior  of  the  solution  of  considered  delay  differential  equation  at  stability  border  is  investigated.  Some  remarks  and  explanation  are  involved  as  well. 

Ключевые  слова:  устойчивость;  дифференциальные  уравнения;  механические  колебания

Keywords:  stability;  delay-differential;  chatter

Процесс  механической  обработки  можно  представить  в  виде  одномерной  модели,  описываемой  дифференциально-разностным  уравнением 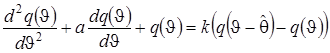 (1).

  (1)

где:  ,  k,  a  —  положительные  постоянные  константы

Поставим  задачу  определить  границу  устойчивости  уравнения  (1)  на  плоскости  параметров    и  k  при  фиксированном  значении  параметра  a.  Для  этого  исследуем  нулевое  состояние  равновесия  на  устойчивость.  Определим  решение  рассматриваемого  уравнения  как  .  Тогда    согласно  [2,  с.  68].  Произведя  такую  замену,  преобразуем  уравнение  (1)  к  виду

   (2)

где:  ;    —  сдвиг  между  фазой    функции  без  запаздывания  и  фазой  функции  запаздывания; 

ω  —  относительная  частота  вибросмещений; 

i  —  мнимая  единица.

Результатом  решения  уравнения  (2)  относительно  ω  является 

    (3)

где  . 

Уравнение  (3)  и  условие  положительности  параметров  k  и  a  приводит  к  набору  ограничений  на  параметры  k  и  a,  которое  гарантирует  дальнейшую  структуру  области  неустойчивости. 

  (4)

Как  показано  в  [1,  с.  23—27]  и  [2,  с.  67—73],  исходное  уравнение  (1)  может  иметь  на  мнимой  оси  только  корни  ±iω₊  и  ±iω_–,  исходя  из  критерия  устойчивости  Найквиста,  при  θ=2πL,  где  L  =0,1,2,…  В  то  же  время  значение  фазового  сдвига  определяется  как 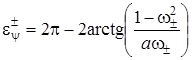   [2,  с.  72].  Исходя  из  вышеизложенного,  получим

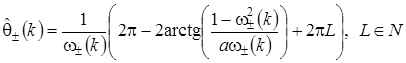  (5)

Очевидно,  что  граница  устойчивости  на  плоскости  параметров    и  k  состоит  из  счетного  числа  подобных  элементов  (L  —  натуральное  число).  Каждый  элемент  границы  будет  складываться  из  двух  несимметричных  половин  —    и  .  Кривые    и    сближается,  только  если  ,  что  возможно  только  в  случае,  когда  ,  где  .  На  рис.  1  приведена  граница  устойчивости  для  значения  параметра  a=0,0512  при  L  =  0,1,2,3,4,5,6,7,8,9. 

Рисунок  1.  Граница  устойчивости  уравнения  (1)  для  a  =0,0512  (сплошной  линией  показаны  значения  ,  пунктирной  —  )

Сделаем  ряд  замечаний  к  приведенным  уравнениям  и  построенной  границе  устойчивости.  Во-первых,  параметры  a  и  k  являются  безразмерными.  Безразмерной  величиной,  следовательно,  также  является  и  относительная  частота  колебаний  ω_±.  Во-вторых,  ограничения  (4)  носят  условный  характер.  Эти  ограничение  определяют  существование  вещественных  корней  на  полуоси  ω>0.  Как  показано,  на  этой  полуоси  ω  имеет  всего  два  корня  ω₊  и  ω_–.  Значение  параметра  k=k₀  задает  предел,  ниже  которого  расположена  зона  устойчивых  решений  и  нет  участков  неустойчивых  решений.  Выше  предела  k=k₀  появляются  зоны  неустойчивости.

Перейдем  к  численному  моделированию  уравнения  (1)  при  заданном  постоянном  значении  a  =0,0512.  Для  численного  решения  дифференциально-разностного  уравнения  применим  модифицированный  метод  Рунге-Кутта  четвертого  порядка  [3,  с.  54].  На  рис.  2  приведены  точки  параметров    и  k  для  проведения  численного  моделирования.

Рисунок  2.  Параметры  для  численного  моделирования    и  k

Набор  точек  соответствует  следующим  парам  A_i(;k_i):  A₀(10,75;  0,0525),  A₁(10,75;  0,1150),  A₂(10,75;  0,0150),  B₀(12,227;  0,1780),  B₁(12,227;  0,3285),  B₂(12,227;  0,1450),  C₀(12,385;  0,3285),  C₁(12,029;  0,4138),  C₂(12,548;  0,2627),  D₀(13,349;  0,2216),  D₁(12,700;  0,3285),  D₂(12,835;  0,1830)

Ниже  представлены  результаты  численного  моделирования  зависимостей  ,  ,  а  также  фазовые  соответствующие  портреты.

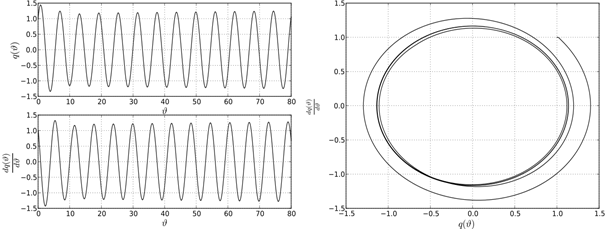
Рисунок  3.  Поведение  системе  в  точке  A₀

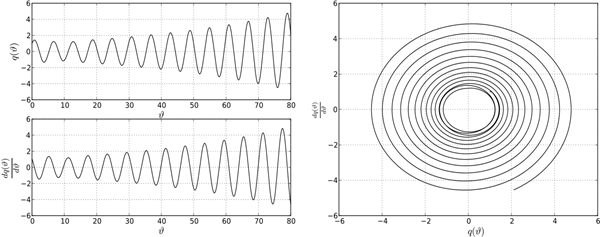
Рисунок  4.  Поведение  системе  в  точке  A₁

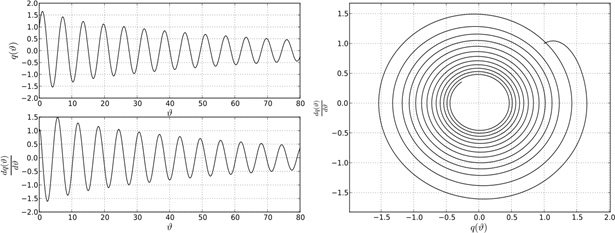
Рисунок  5.  Поведение  системе  в  точке  A₂

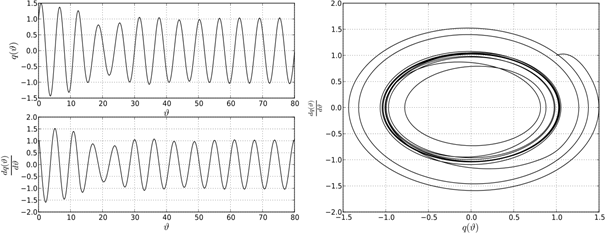
Рисунок  6.  Поведение  системе  в  точке  B₀

Рисунок  7.  Поведение  системе  в  точке  B₁

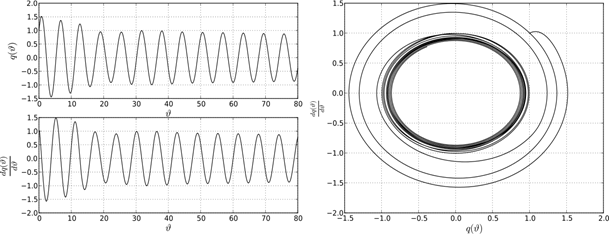
Рисунок  8.  Поведение  системе  в  точке  B₂

Рисунок  9.  Поведение  системе  в  точке  C₀

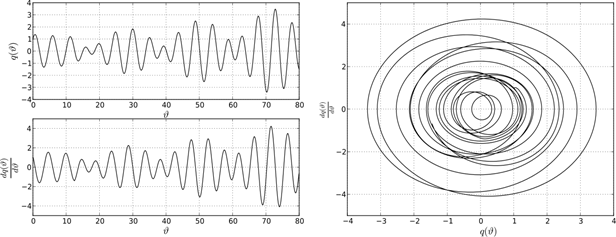
Рисунок  10.  Поведение  системе  в  точке  C₁

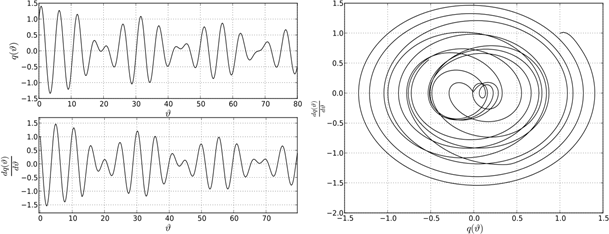
Рисунок  11.  Поведение  системе  в  точке  C₂

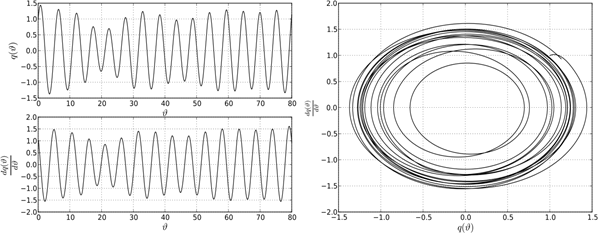
Рисунок  12.  Поведение  системе  в  точке  D₀

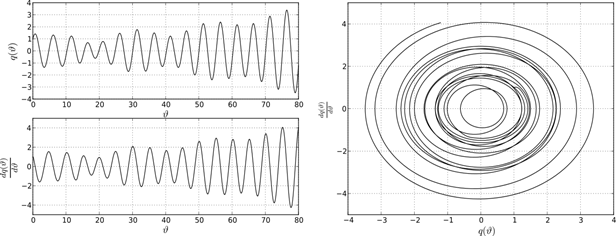
Рисунок  13.  Поведение  системе  в  точке  D₁

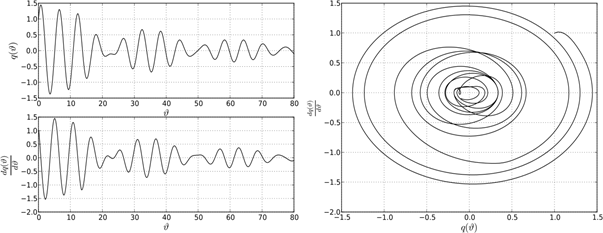
Рисунок  14.  Поведение  системе  в  точке  D₂

Сделаем  выводы.  Поведение  решений  дифференциально-разностного  уравнения  (1)  на  границе  устойчивости  характеризуется  существованием  предельных  устойчивых  циклов.  Однако  предельные  циклы  не  подобны  между  собой.  Описанная  структура  устойчивых  и  неустойчивых  решений  уравнения  (1)  при  различных  парах  параметров    и  k  указывает  на  существование  некоторой  «области  притяжения»  точки  пересечения  С₀,  в  которой  появляются  и  существуют  биения.  В  общем  случае,  биения  возникают  в  результате  наложения  двух  периодических  колебаний  близких  по  частоте  в  системе  двух  осцилляторов.  В  системе  с  одной  степенью  свободы  роль  второго  осциллятора  играет  функция  запаздывания,  которая,  как  указано  выше,  отстает  по  фазе  от  основной  функции  на  величину  .  Заметим,  что  при  значениях    . 

Список  литературы:

1.Красильников  А.Я.,  Кравченко  К.Ю.  Аналитические  методы  исследования  устойчивости  систем  с  запаздыванием,  описывающие  процесс  фрезерования  //  Справочник.  Инженерный  журнал  с  приложением.  —  2013.  —  №  9  —  С.  23—31.

2.Красильников  А.Я.,  Кравченко  К.Ю.  Исследование  устойчивости  систем  с  запаздыванием,  описывающих  процесс  фрезерования,  в  случае  с  одной  степенью  свободы  //  Вестник  машиностроения.  —  2013.  —  №  9  —  С.  67—75.

3.Красильников  А.Я.,  Кравченко  К.Ю.  Модифицированный  метод  Ренге-Кутта  для  решения  дифференциальных  уравнений  с  отклоняющимся  аргументом  //  Перспективы  развития  информационных  технологий:  сборник  материалов  XIII  Международной  научно-практической  конференции  (Новосибирск,  24  июня  2013  г.).  Новосибирск,  2013.  —  С.  53—57.