ДИНАМИЧЕСКИЕ  ХАРАКТЕРИСТИКИ  УПРАВЛЯЕМЫХ  ДЕБАЛАНСНЫХ  ВИБРОВОЗБУДИТЕЛЕЙ

Черевко  Александр  Николаевич

канд.  техн.  наук,  зав.  кафедрой  теоретической  механики,

доцент  Полтавского  национального  технического  университета,  г.  Полтава

E-mail: 

DYNAMIC  CHARACTERISTICS  OF  CONTROLLED  DEBALANCE  VIBRATION  EXCITERS

Alexandr  Cherevko

candidate  of  Science,  Head  of  Theoretical  Mechanics  department,  assistant  professor  of  Poltava  National  Technical  University,  Poltava

АННОТАЦИЯ

Управляемые  дебалансные  вибровозбудители  —  основа  технологических  машин  будущего.  Генератор  колебаний  позволяет  получать  разнообразные  нестационарные  вибрационные  поля  переменной  структуры.  Для  оценки  возможностей  управляемого  вибровозбудителя  используется  теория  приведения  системы  сил  к  заданному  центру.  В  результате  проведенных  исследований  были  построены  графики  зависимостей  динамических  характеристик  силового  поля  от  угла  поворота  подвижного  дебаланса.

ABSTRACT

Controlled  unbalance  vibration  exciters  -  the  basis  of  machinery  technology  of  the  future.  The  oscillator  produces  a  variety  of  non-stationary  vibrational  fields  of  variable  structure.  To  assess  the  opportunities  managed  exciter  theory  is  used  to  bring  the  system  of  forces  to  a  given  center.  The  studies  were  plotted  dynamic  characteristics  of  power-th  field  of  the  angle  of  rotation  of  the  movable  eccentric  weight.

Ключевые  слова:  дебаланс;  вибровозбудитель,  силовое  поле.

Keywords:  eccentric  weight,  vibration  exciter,  the  force  field. 

В  качестве  привода  вибрационной  машины  может  использоваться  управляемый  вибровозбудитель  с  тремя  дебалансами  [1—2].  В  начальный  момент  времени,  который  совпадает  с  моментом  пуска  машины,  он  представляет  собой  динамически  уравновешенную  систему.  Дальнейшая  работа  машины  связана  с  перемещением  подвижных  дебалансов  вдоль  дебалансного  вала  по  направлению  винтовых  канавок.

Рассмотрим  несколько  возможных  случаев:

1.  направление  поворота  подвижных  дебалансов  совпадают  (против  часовой  стрелки,  если  смотреть  навстречу  оси  )  (рис.  1а); 

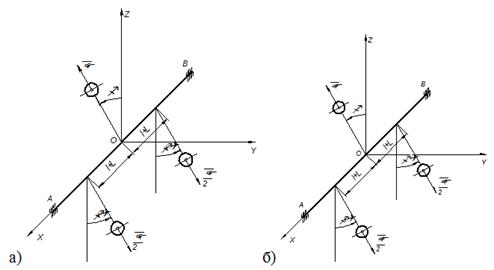
Рисунок  1.  Схема  управляемого  трехдебалансного  вибровозбудителя:  а)  направление  поворота  подвижных  дебалансов  совпадают;  б)  направление  поворота  подвижных  дебалансов  противоположны

Для  определения  возможностей  вибровозбудителя  приведем  систему  сил  инерции  к  простейшему  виду.

Определим  главный  вектор  сил  инерции  :

.

Проекции  главного  вектора  на  оси  координат  определяются  по  следующим  формулам:

;    

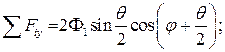
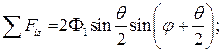;         (рис.  2).

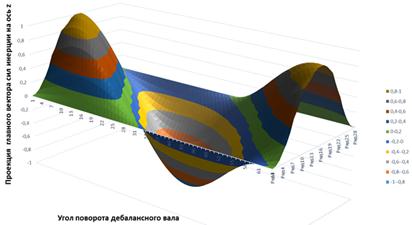
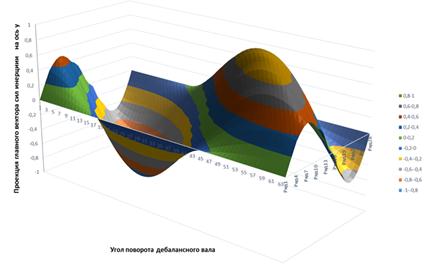
Рисунок  2.  Изменение  проекций  главного  вектора  сил  инерции  на  оси  координат

. ;  (рис.  3а).

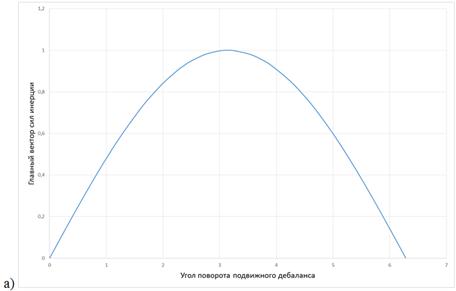
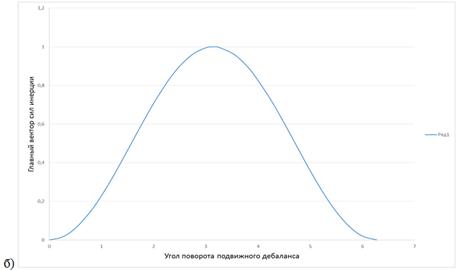
Рисунок  3.  Изменение  главного  вектора  сил  инерции:  а)  направление  поворота  подвижных  дебалансов  совпадают;  б)  направление  поворота  подвижных  дебалансов  противоположны

Определим  главный  момент  сил  инерции  .

;

где:     ;        ;       .

;   ;  ;  .

Таким  образом,  система  сил  приводится  к  равнодействующей  в  центре  приведения  ,   .

Определим  направляющие  косинуси  равнодействующей:

;    .

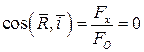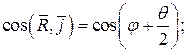
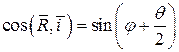2.  направление  поворота  подвижных  дебалансов  противоположны  (рис.  1б);

Приведем  систему  сил  к  центру  . 

Главный  вектор  системы  сил    имеет  следующие  проекции  на  оси  координат:

;            ;  

;      (рис.4).

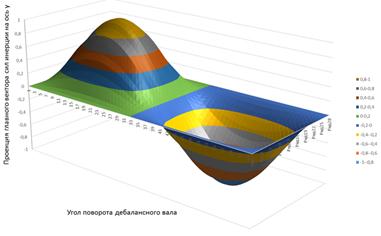
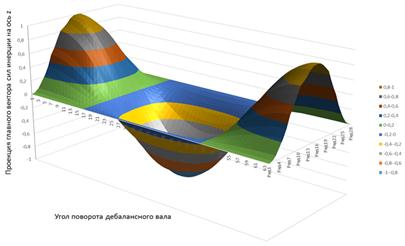
Рисунок  4.  Изменение  проекций  главного  вектора  сил  инерции  на  оси  координат

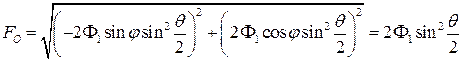  (рис.3б).

Проекции  главного  момента    на  оси  координат  определяться  по  следующим  формулам:

;    

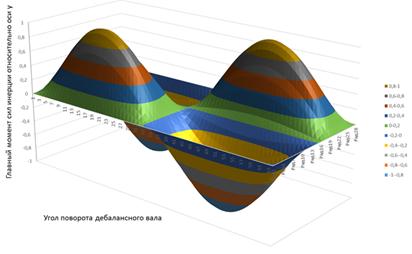
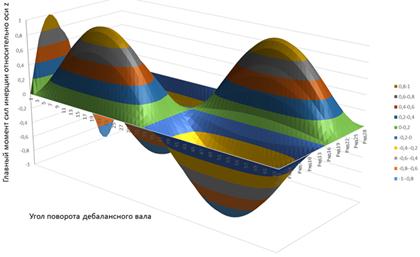
Рисунок  5.  Изменение  проекций  главного  момента  сил  инерции  на  оси  координат

Определим  главный  момент    системы  сил:

.

Для  оценки  возможностей  вибровозбудителя  по  синтезу  вибрационных  полей,  определим  наименьший  главный  момент  системы  сил:

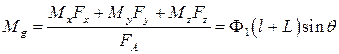
Таким  образом,  система  сил  может  приводиться  к  динамическому  винту  с  параметром:

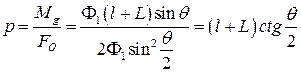
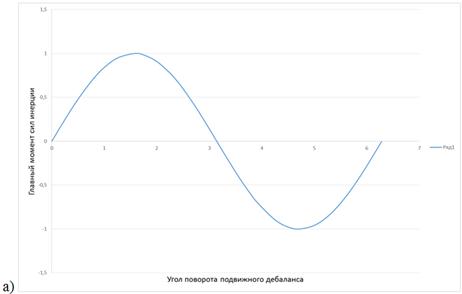
Рисунок  6.  Изменение  динамических  параметров  вибровозбудителя:  а)главного  момента  сил  инерции;  б)  параметра  динамического  винта

Определим  уравнение  центральной  винтовой  оси:

.     .

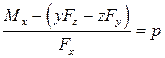Исследуем,  когда  полученное  уравнение  выполняется:

1)                    ;    ;     ;

В  этом  случае  ; ;  и  система  находится  в  динамическом  равновесии.

2)                    ;       .

;  .

;  .

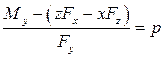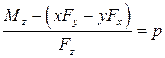Таким  образом,  получены  следующие  уравнения  оси:

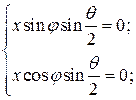
Решим  эту  систему:

а)  ;

б)  ;  ;         ,    —  система  находится  в  динамическом  равновесии,  поэтому  этот  корень  не  подходит;

в)  если  ,  то  необходимо,  чтобы  и  ,  а  это  невозможно;

г)   если  ,  то  дополнительно  должно  быть  и  ,  а  это,  как  показано  выше,  в  данной  задаче  невозможно.

Принимаем  .

Система  сил  инерции  не  приводится  к  динамическому  винту,  когда  .  Таким  образом,  должно  быть:  .  Уравнение  выполняется  тогда,  когда:  ,  а  .

При  система  сил  находится  в  динамическом  равновесии,  а  при  ,  ,    и  система  сил  приводится  к  равнодействующей,  приложенной  в  старом  центре  приведения.  Проекции  равнодействующей  на  оси  координат  имеют  вид:

; ;

.

Случай  приведения  системы  сил  к  паре  сил  невозможен,  так  как:

,  при  ,  но  в  этом  случае  .

Выводы.

При  изменении  угла  поворота    подвижных  дебалансов  в  пределах  от    до    система  сил  инерции  приводится  к  различным  простым  видам:

1.  ,  система  сил  находится  в  динамическом  равновесии;

2.  ,  система  сил  приводится  к  правому  динамическому  винту  с  параметром  ;

3.  ,  система  сил  приводится  к  равнодействующей,    приложенной  в  старом  центре  приведения;

4.  ,  система  сил  приводится  к  левому  динамическому  винту  с  параметром  .  Может  показаться  на  первый  взгляд,  что  изменение  угла  поворота  подвижных  дебалансов  в  этих  пределах,  ничем  не  отличается  от  пункта  б.  Однако,  это  не  так.  Происходит  изменение  направления  динамического  винта  в  процессе  работы  технологической  машины;

5.  ,  система  сил  находится  в  динамическом  равновесии.

Список  литературы:

1.Бабичев  А.П.  Основы  вибрационной  технологии  /  А.П.  Бабичев,  И.А.  Бабичев.  Ростов-н/Д.:  ДГТУ,  1999.  —  620  с.

2.Сердюк  Л.И.  Основы  теории,  расчет  и  конструирование  управляемых  вибрационных  машин  с  дебалансными  возбудителями:  автореф.  дис.  докт.  техн.  наук  /  Л.И.  Сердюк;  ХПИ.  Харьков,  1991.  —  48  с.