ПОСТРОЕНИЕ  ФУНКЦИИ  ПРИНАДЛЕЖНОСТИ  НЕЧЕТКИХ  МНОЖЕСТВ

Кочеткова  Инесса  Андреевна

старший  преподаватель  БГТУ  им.  В.Г.  Шухова,  г.  Белгород

E-mail:  IneSuan@gmail.com

Иванов  Игорь  Владимирович

канд.  техн.  наук,  доцент  БГТУ  им.  В.Г.  Шухова,  г.  Белгород

E-mail: 

BUILDING  FUNCTIONS  OF  FUZZY  SETS

Kochetkova  Inessa  Andreevna

senior  teacher  of  BSTU  named  after  V.G.  Shukhov,  Belgorod

Ivanov  Igor  Vladimirovich

candidate  of  Technical  Sciences,  Associate  Professor  of  BSTU  named  after  V.G.  Shukhov,  Belgorod

АННОТАЦИЯ

Рассмотрено  расширение  функциональных  возможностей  ранее  разработанного  нами  метода  распознавания  образов  на  основе  представления  многомерных  форм  классов  образов  в  двумерные  в  интересах  диагностики  путем  построения  функций  принадлежности  и  использования  теории  нечетких  множеств,  позволяющих  определять  степени  принадлежности  точки,  характеризующей  состояние,  к  классу  допустимых  состояний  для  случая  пересечения  классов  в  исходном  пространстве 

ABSTRACT

Consider  the  extended  functionality  of  the  earlier  of  our  method  of  image  recognition  based  on  representation  of  multi-dimensional  shapes  in  two-dimensional  images  of  the  classes  in  the  interests  of  diagnosis  by  constructing  membership  functions  and  the  use  of  fuzzy  set  theory  can  help  determine  the  degree  of  implement  point  that  characterizes  the  state,  to  the  class  of  admissible  states  for  the  case  of  the  intersection  of  classes  in  the  original  space

Ключевые  слова:  распознавание  образов;  класс;  конфигурация;  нечеткие  множества;  степени  принадлежности;  обработка  данных;  диагностика.

Keywords:  image  recognition;  class;  configuration;  fuzzy  sets;  membership  degrees,  the  processing  of  data;  diagnosis.

Решение  задачи  диагностики  состояний  сложных  объектов  [1]  основывается  на  анализе  и  интерпретации  имеющихся  данных  о  текущем  состоянии  подсистемы  и  предыстории  его  состояний.  В  настоящей  статье  рассматривается  один  из  возможных  подходов  к  решению  задачи  автоматизации  процедуры  распознавания  состояния  по  предварительно  построенному  многомерному  виртуальному  образу  состояния  (А_N(t)),  и  многомерным  классам  диагнозов  В_i  [2,  с.  79,  3],  путем  построения  функций  принадлежности.  Класс  диагнозов  составляют  наборы  признаков  пациентов,  имеющих  одно  для  всех  выделенное  именем  состояние.  Возможным  решением  упомянутой  выше  задачи  является  использование  геометрического  метода  формирования,  визуализации  и  интерактивного  распознавания  многомерных  образов  сложных  систем  [2,  с.  79,  3].  Одной  из  основных  процедур  данного  метода  является  процедура  формирования  двумерного  образа  состояния  ()  и  двумерных  образов  классов  состояний  В_2i,  представляющих  собой  проекции  А_N(t)  и  В_i  на  плоскость  {}  (рис.  1),  совпадающую  с  плоскостью  отображающего  многоцветного  экрана  видеомонитора. 

Однако  при  практической  реализации  метода,  описанного  в  [2,  с.  79,  3],  возможны  ситуации,  обуславливающие  неоднозначность  принятия  управленческого  решения  о  текущем  состоянии  объекта.  Такие  ситуации  могут  появляться  в  связи  с  тем,  что  в  N-мерном  пространстве  состояний  многомерные  классы  диагнозов  В_i  могут  совпадать,  что,  в  свою  очередь,  обусловливает  пересечение  классов  состояний  В_2i  друг  с  другом.  В  этих  случаях  значение  А₂(t)  может  находиться  в  области  пересечения  двух  и  более  В_2i  (рис.  1)  —  . 

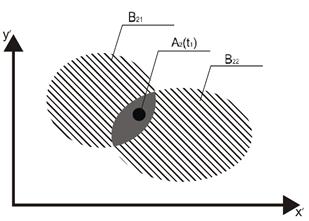
Рисунок  1.  Топология  взаимного  положения  на  плоскости  {}  двух  виртуальных  двумерных  классов  диагнозов  с  фактическим  пересечением  в  многомерном  пространстве  признаков

В  связи  с  этим  рассмотрим  для  этой  ситуации  возможность  уменьшения  степени  неоднозначности  распознавания  ,  применяя  теорию  нечётких  множеств,  которая  позволяет  количественно  оценивать  значение  степени  принадлежности  текущего  значения  двумерного  образа  состояния  объекта  соответствующему  образу    в  области  их  фактического  пересечения  друг  с  другом.  Такой  подход  предусматривает  проведение  определённой  совокупности  процедур  [1].  При  этом  классы  диагнозов  и  виртуальный  образ  состояния  объекта  (кортеж  признаков)  рассматриваются  в  многомерном  признаковом  пространстве  —  В_i  и  ,  где    —  значение  А_N(t),  находящиеся  в  области  пересечения  двух  и  более  В_i.  На  первом  этапе  определяют  функции  принадлежности  для  каждого  терма  лингвистических  переменных,  характеризующих  .  В  связи  с  этим,  все  признаки  задаются  как  лингвистические  переменные.  Далее  определяется,  какой  из  термов  лингвистической  переменной  соответствует  тому  или  иному  классу  диагнозов  .

Для  построения  функций  принадлежности  воспользуемся  методом  основанном  на  использовании  статистических  данных. 

Пусть  имеется  список  симптомов  с  их  показателями  для  конкретных  заболеваний.  Шкала  симптомов  разбивается  на  фиксированные  интервалы  (например,  шкала  симптома  Систолическое  артериальное  давление  (САД)  —  разбивается  на  интервалы  100—110,  110—120,  …  190—200).  Предположим,  что  наблюдая  за  n  объектами  (пациентами)  в  течение  некоторого  времени  устанавливается  m  диагнозов.  По  итогам  наблюдения  эксперт  фиксирует  частоту  попадания  определенного  интервала  симптома  в  заболевание.  На  основании  этих  статистических  данных  строится  гистограмма  (рис  2.).

Таблица  1. 

Частоты  попадания  определенного  интервала  симптома  в  заболевание

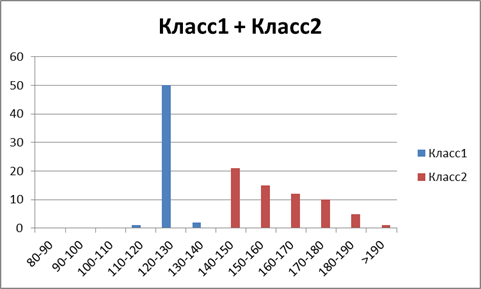
Рисунок  2.  Гистограмма  статистических  данных  по  симптому  САД

На  универсальной  шкале  [0,1]  необходимо  разместить  значения  интервалов  по  каждому  симптому.  Тогда  степень  принадлежности  некоторого  значения  вычисляется  как  отношение  числа  экспериментов,  в  которых  оно  встречалось  в  определенном  интервале  шкалы,  к  максимальному  для  этого  значения  числу  экспериментов  по  всем  интервалам. 

Матрица  оценки  показаний  имеет  вид,  в  табл.  2.

Таблица  2. 

Матрица  оценки  показаний

Для  построения  функций  принадлежности  находятся  максимальные  элементы  по  строкам  матрицы  оценки  показаний  по  формулам:

          (1)

                                (2)

где  c_ij  элементы  матрицы  оценки  показаний.

Значения  функций  принадлежности  μ_ij  приведены  в  табл.  3.

Таблица  3. 

Матрица  оценки  значений  функций  принадлежности

Таким  образом,  рассмотрен  один  из  возможных  подходов  к  совершенствованию  метода  распознавания  состояния  объектов  в  ситуации,  характеризующейся  пересечением  В_2i  друг  с  другом  в  многомерном  пространстве  признаков.  Решение  задачи  базируется  на  совместном  использовании  проективно-геометрического  метода  распознавания  образов  и  теории  нечетких  множеств,  которая  позволяет  осуществить  количественную  оценку  степени  принадлежности  текущего  значения  каждого  из  параметров  состояния  G_q  (А₂(t))  к  каждому  из  классов  состояний  в  соответствующей  точке,  принадлежащей  области  пересечения  В_2i.  Предложенное  решение  можно  рассматривать  как  новый  подход  к  организации  поддержки  принятия  решений,  позволяющий  автоматизировать  мониторинг,  оперативный  контроль  или  анализ  закономерностей  изменения  возникающих  в  сложных  системах.

Преимуществом  предлагаемого  подхода,  сущность  которого  заключатся  в  том,  что  вначале  определяются  зоны  пересечений  классов  диагнозов  в  многомерном  пространстве  признаков  путем  использования  ранее  разработанного  метода  распознавания,  а  затем  только  для  этих  областей  пересечений  применяется  аппарат  теории  нечетких  множеств,  что  существенно  сокращает  время  опроса  экспертов  и  нагрузку  на  каждого  из  них,  а  также  устраняются  многие  варианты  отказа  от  диагностики.

Список  литературы:

1.Алтунин  А.Е.,  Семухин  М.В.  Модели  и  алгоритмы  принятия  решений  в  нечетких  условиях.  Тюмень:  Изд.  Тюменского  государственного  университета,  2000.  —  352  с.

2.Довгаль  В.М,  Старков  Ф.А.,  Классификация  и  распознавание  точечных  образов  с  помощью  визуализации  многомерных  объектов//  Известия  Курского  государственного  технического  университета.  —  2007.  —  №  4(21).  —  С.  78—80.

3.Способ  распознавания  состояния  сердечно-сосудистой  системы  по  его  многомерному  образу  /  В.М.  Довгаль,  В.М.  Никитин,  Е.А.  Липунова,  И.А.  Кочеткова  //  Компьютерные  науки  и  технологии:  Вторая  междунар.  науч.-технич.  конф.,  (Белгород,  3—5  октября  2011  г.  ),  Белгород  :  Изд-во  ООО  «ГиК»,  2011.  —  С.  193—198.