ВАРИАТИВНОЕ  ДИСКРЕТНОЕ  ГЕОМЕТРИЧЕСКОЕ  МОДЕЛИРОВАНИЕ  ОДНОМЕРНЫХ  ОБВОДОВ  НА  ОСНОВЕ  ПРОСТРАНСТВЕННЫХ  УГЛОВЫХ  ПАРАМЕТРОВ

Гавриленко  Евгений  Андреевич

канд.  техн.  наук,  докторант  Таврического  государственного  агротехнологического  университета  г.  Мелитополь  (Украина)

E-mail:eagavrilenko@mail.ru

Найдыш  Андрей  Владимирович

д-р  техн.  наук,  профессор  Мелитопольского  государственного  педагогического  университета  им.  Богдана  Хмельницкого  г.  Мелитополь  (Украина)

E-mail: 

VARIATIVE  DISCRETE  GEOMETRIC  MODELING  OF  ONE-DIMENSIONAL  CONTOURS  BASED  ON  THE  BASIS  OF  THE  SPACE  ANGULAR  PARAMETERS

Eugene  Gavrilenko

candidate  of  Technical  Sciences,  Doctoral  Candidate  of  Tavria  State  Agrotechnological  University,  Melitopol  (Ukraine)

Andrew  Naydysh

doctor  of  Technical  Sciences,  Professor  of  Melitopol  State  Pedagogical  University  named  after  Bogdan  Khmelnitsky,  Melitopol  (Ukraine)

АННОТАЦИЯ

Предложен  алгоритм  формирования  гладкой  пространственной  кривой  по  заданным  условиям.  Основой  алгоритма  является  анализ  исходного  точечного  ряда,  в  результате  которого  определяется  область  возможного  расположения  кривой  и  диапазоны  возможных  значений  её  геометрических  характеристик.  Существует  возможность  пошагового  контроля  и  коррекции  получаемого  решения,  наложения  на  него  дополнительных  условий,  гарантируется  отсутствие  осцилляции.

ABSTRACT

The  algorithm  of  formation  a  smooth  space  curve  on  the  defined  conditions  is  proposed  in  this  article.  Basis  for  the  algorithm  is  the  analysis  of  initial  points  set,  a  result  of  which  the  area  of  possible  location  of  the  curve,  and  the  ranges  of  possible  values  of  its  geometrical  characteristics  are  determined.  It  is  possible  to  control  and  correct  the  solution  which  obtains  at  each  step  of  modeling,  to  impose  on  the  decision  a  additional  conditions  and  to  ensure  the  absence  of  oscillations.

Ключевые  слова:  дискретно  представленная  кривая;  сгущение  точечного  ряда;  радиус  кривизны;  кручение.

Keywords:  discretely  represented  curve;  thickening  of  points  set;  radius  of  curvature;  torsion.

Пространственные  одномерные  обводы  используются  в  качестве  элементов  определителя  дискретно  представленной  поверхности.  При  моделировании  поверхностей  с  повышенными  динамическими  свойствами  необходимо  обеспечить  контроль  направления  хода  кривой,  закономерное  изменение  кривизны  и  кручения,  второй  порядок  гладкости  обвода  [2].  Повышенные  динамические  качества  необходимы  поверхностям,  ограничивающим  корпусные  изделия  авиа-,  автомобиле-,  судостроения,  лопатки  турбин  и  смесителей,  каналы  двигателей  внутреннего  сгорания,  трубопроводы,  рабочие  органы  сельскохозяйственных  машин.

Для  эффективного  решения  задачи  необходимы  методы,  обеспечивающие  заданную  точность  формирования  геометрических  характеристик  обводов,  локальность  корректировок,  отсутствие  осцилляции.  Указанным  требованиям  отвечает  вариативное  дискретное  геометрическое  моделирование,  предполагающее  формирование  обвода  в  виде  сколь  угодно  большого  количества  точек,  получаемых  в  результате  последовательных  сгущений  исходного  точечного  ряда  [1].

Гладкая  пространственная  дискретно  представленная  кривая  (ДПК)  формируется  сгущением  упорядоченного  множества  точек.  Каждые  три  последовательные  точки  исходного  ряда  определяют  плоскость.  Будем  называть  эти  плоскости  прилегающими  (ППi).  Потребуем,  чтобы  величина  двугранного  угла,  ограниченного  смежными  ПП  (φ_i),  внутри  которого  расположен  участок  ДПК  не  превышала  180  градусов.  Тогда,  по  расположению  ПП  можно  судить  о  направлении  хода  кривой.  ДПК  разбивается  на  участки  правого  и  левого  хода  и  формируется  отдельно,  по  этим  участкам.  Касательная  к  ДПК  (t_i)  располагается  внутри  двух  смежных  углов  (φ_i-1  и  φ_i)  одновременно.  Она  может  быть  задана  как  линия  пересечения  плоскостей,  касательных  с  ДПК  в  точке  i  (’КП_і  и  КП_і’).  Положение  касательных  плоскостей  определяется  прохождением  через  хорду  сопровождающей  ломаной  линии  ([і-1;i],[i;  і+1])  и  углом,  образуемым  с  соответствующей  прилегающей  плоскостью  (рисунок  1).

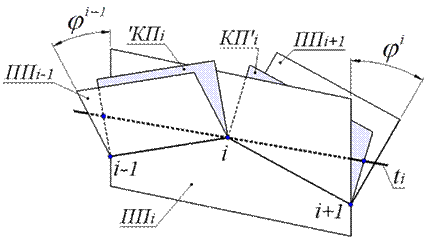
Рисунок  1.  Определение  положения  касательных  прямых

Плоскости  касательные  с  ДПК  в  одной  точке,  определяют  диапазон  возможного  расположения  соприкасающейся  плоскости  (на  рисунке  2  –  двугранный  угол  ω).

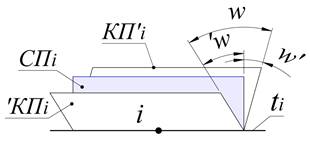
Рисунок  2.  Диапазон  расположения  соприкасающейся  плоскости

Назначив  в  исходных  точках  соприкасающиеся  плоскости  (СП_i),  мы  задаём  в  них  положение  основных  трёхгранников.  Далее  ДПК  формируется  как  обвод  первого  порядка  фиксации.  Положение  плоскостей,  касательных  с  ДПК  в  исходных  точках  и  проходящих  через  точку  сгущения  (),  назначается  по  центру  двугранного  угла,  ограниченного  соприкасающейся  и  исходной  касательной  плоскостями.  Точка  сгущения  (i_сг)  назначается  на  прямой  пересечения  указанных  плоскостей  (рисунок  3).

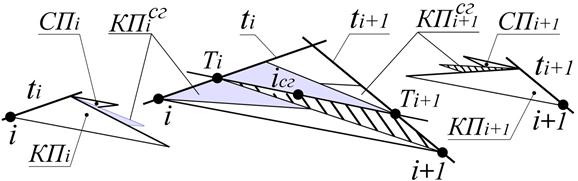
Рисунок  3.  Определение  положения  точки  сгущения

В  процессе  последовательных  сгущений  точечного  ряда,  хорда  сопровождающей  ломаной  линии,  ограниченная  исходной  точкой  и  ближайшей  к  ней  точкой  сгущения  стремится  занять  положение  касательной  к  ДПК.  Касательная  плоскость,  определяемая  касательной  прямой  в  исходной  точке  и  ближайшей  точкой  сгущения,  стремится  к  положению  соприкасающейся  плоскости.  Назначение  касательных  прямых,  соприкасающихся  плоскостей  и  точек  сгущения  внутри  соответствующих  диапазонов  обеспечивает  первый  порядок  гладкости  формируемой  ДПК.

При  формировании  ДПК  второго  порядка  гладкости,  значения  кручения  (B_i)  и  радиусов  кривизны  (R_i)  оцениваются  с  помощью  их  дискретных  аналогов.

Дискретное  кручение  ()  на  -м  участке  ДПК  определяется  по  формуле:

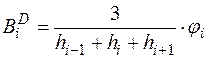  ,                                (1)

где:  ,  —  величина  двугранного  угла  расположения  ДПК;

  —  длина  хорды  сопровождающей  ломаной  линии.

Значения  дискретного  кручения  позволяют  определить  диапазоны  значений  и  направление  возрастания  кручения  вдоль  ДПК:

.               (2)

Значения  радиуса  кривизны  в  i-й  точке  ДПК  оценивается  радиусом  касательной  окружности,  определяемой  точкой  ,  касательной  прямой  в  этой  точке  и  ближайшей  точкой  ДПК.  В  первом  приближении  это  окружности  радиусов    и  ,  проходящие  через  точки    и    соответственно.  Значения  радиусов  касательных  окружностей  задают  диапазоны  возможных  значений  и  направление  возрастания  радиусов  кривизны  вдоль  ДПК.

.          (3)

Положение  касательных  плоскостей,  касательных  прямых  и  соприкасающихся  плоскостей  уточняется  внутри  диапазонов  их  возможного  расположения,  исходя  из  динамики  изменения  значений  дискретного  кручения  и  радиусов  касательных  окружностей.  Выполнение  этих  условий  обеспечивает  наличие  в  точках  ДПК  диапазонов  (возможных  по  условиям  задачи)  значений  радиусов  кривизны  и  кручения.  В  процессе  последовательных  сгущений  диапазоны  кривизны  и  кручения  уменьшаются  и  сходятся  к  значениям,  закономерно  изменяющимся  вдоль  ДПК.

Полученные  алгоритмы  могут  быть  основой  для  создания  программного  обеспечения,  совместимого  с  существующими  CAD-пакетами  через  интерфейс  API.

Список  литературы:

1.Найдиш  В.М.  Дискретна  інтерполяція:  учеб.  пособие.  Мелітополь,  2008.  —  250  с.

2.Осипов  В.А.  Машинные  методы  проектирования  непрерывно-каркасных  поверхностей.  М.:  Машиностроение,  1979.  —  248  с.