Статья опубликована в рамках: XXIII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 10 июля 2013 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОЦЕНИВАНИЕ НЕИЗВЕСТНЫХ ПАРАМЕТРОВ В ЗАДАЧЕ АКТИВНОЙ ПАРАМЕТРИЧЕСКОЙ ИДЕНТИФИКАЦИИ СТОХАСТИЧЕСКИХ НЕЛИНЕЙНЫХ НЕПРЕРЫВНО-ДИСКРЕТНЫХ СИСТЕМ
Филиппова Елена Владимировна
магистр прикладной математики и информатики, аспирантка кафедры прикладной математики Новосибирского государственного технического университета, г. Новосибирск
E-mail: alena-filippova@mail.ru
ESTIMATION OF THE UNKNOWN PARAMETER IN THE ACTIVE PARAMETRICAL IDENTIFICATION OF STOCHASTIC NONLINEAR CONTINUOUS-DISCRETE SYSTEMS
Filippova Elena
master of applied mathematics and computer science, post-graduate student of applied mathematics department of the Novosibirsk state technical university, Novosibirsk
АННОТАЦИЯ
Представлены оригинальные алгоритмы вычисления критерия максимального правдоподобия и его градиента для стохастических нелинейных непрерывно-дискретных систем, описывающихся моделями в пространстве состояний в задаче активной параметрической идентификации.
ABSTRACT
For stochastic nonlinear continuous-discrete systems are described of models in the state space the original algorithms for computing the maximum likelihood and its gradient are shown.
Ключевые слова: оценивание параметров; метод максимального правдоподобия.
Keywords: parameter estimation; the method of maximum likelihood.
Процедура активной идентификации при предварительно выбранной модельной структуре предполагает выполнение следующих основных этапов [1, 2, 6]:
1. Оценивание неизвестных параметров, входящих в модель, по измерительным данным, соответствующим определенному пробному сигналу,
2. Синтез на основе полученных оценок оптимального по некоторому выбранному критерию сигнала (планирование эксперимента),
3. Пересчет оценок неизвестных параметров по измерительным данным, соответствующим синтезированному сигналу.
В настоящей работе приведены вычислительные алгоритмы, связанные с оцениванием неизвестных параметров, входящим в первый и третий этапы процедуры активной идентификации.
Рассмотрим следующую модель непрерывно-дискретной системы:
![]() ;(1)
;(1) ![]() (2)
(2)
где: ![]() — n-вектор состояния;
— n-вектор состояния;
![]() — детерминированный r-вектор управления (входа);
— детерминированный r-вектор управления (входа);
![]() — p-вектор возмущения;
— p-вектор возмущения;
![]() — m-вектор измерения (выхода);
— m-вектор измерения (выхода);
![]() — m-вектор ошибки измерения.
— m-вектор ошибки измерения.
Будем считать, что белые шумы ![]() и
и ![]() взаимно некоррелированы и не коррелируют с начальным состоянием
взаимно некоррелированы и не коррелируют с начальным состоянием ![]() , причем
, причем ![]() ,
, ![]() и
и ![]() , неизвестные параметры сведены в вектор
, неизвестные параметры сведены в вектор ![]() , включающий в себя элементы вектор - функций
, включающий в себя элементы вектор - функций ![]() ,
, ![]() , матриц
, матриц ![]() ,
, ![]() ,
, ![]() ,
, ![]() и вектора
и вектора ![]() в различных комбинациях.
в различных комбинациях.
Частным случаем модели (1), (2) являются модели линейной нестационарной системы
![]() ; (3)
; (3)
![]()
![]() , (4)
, (4)
При активной параметрической идентификации нелинейных систем (1), (2) с указанными априорными предположениями будем применять временную [6] и статистическую [1] линеаризации, в результате сводя задачу активной параметрической идентификации к соответствующей задаче для модели вида (3), (4) со специальным образом определенными векторами ![]() ,
, ![]() и матрицами
и матрицами ![]() ,
, ![]() .
.
Оценивание неизвестных параметров математической модели (1), (2) будем осуществлять по данным наблюдений ![]() в соответствии с критерием идентификации
в соответствии с критерием идентификации ![]() . Сбор числовых данных происходит в процессе проведения идентификационных экспериментов, которые выполняются по некоторому плану
. Сбор числовых данных происходит в процессе проведения идентификационных экспериментов, которые выполняются по некоторому плану ![]() .
.
Предположим, что экспериментатор может произвести ![]() независимых запусков системы, причем сигнал
независимых запусков системы, причем сигнал ![]() он подает на вход системы
он подает на вход системы ![]() раз, сигнал
раз, сигнал ![]() —
— ![]() раз и т. д., наконец, сигнал
раз и т. д., наконец, сигнал ![]() —
— ![]() раз. В этом случае дискретный (точный) нормированный план эксперимента
раз. В этом случае дискретный (точный) нормированный план эксперимента ![]() представляет собой совокупность точек
представляет собой совокупность точек ![]() ,
,![]() ,…,
,…,![]() (спектр плана) и соответствующих им долей повторных запусков:
(спектр плана) и соответствующих им долей повторных запусков:
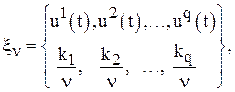
![]() ,
, ![]() ,
, ![]() .
.
Обозначим через ![]() j-ю реализацию выходного сигнала (
j-ю реализацию выходного сигнала (![]() ), соответствующую i-му входному сигналу
), соответствующую i-му входному сигналу ![]() (i=1,2,…,q). Тогда в результате проведения по плану
(i=1,2,…,q). Тогда в результате проведения по плану ![]() идентификационных экспериментов будет сформировано множество
идентификационных экспериментов будет сформировано множество
 .
.
Уточним структуру ![]() :
:
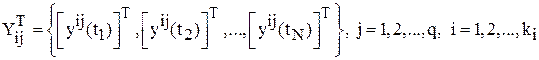 ,
,
и заметим, что при пассивной параметрической идентификации часто встречаются случаи, когда ![]() .
.
Априорные предположения, сделанные выше, и выполненная линеаризация, позволяют воспользоваться методом максимального правдоподобия (ММП) для оценивания неизвестных параметров, являющимся одним из наиболее универсальных и эффективных методов параметрического оценивания. Оценки, полученные методом максимального правдоподобия (ОМП), обладают хорошими асимптотическими свойствами, проявляющиеся для больших объемов выборок, а именно: при условии регулярности модели ОМП являются асимптотически несмещенными, состоятельными, асимптотически эффективными и асимптотически нормальными [3]. В соответствии с ММП необходимо найти такие значения параметров ![]() , для которых
, для которых
![]() , (5)
, (5)
где в соответствии с [8, 9]:
![]()
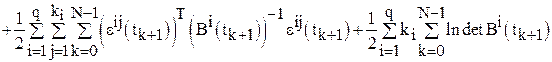 , (6)
, (6)
причем ![]() и
и ![]() определяются по следующим рекуррентным уравнениям непрерывно-дискретного фильтра Калмана [5]:
определяются по следующим рекуррентным уравнениям непрерывно-дискретного фильтра Калмана [5]:
![]() ; (7)
; (7)
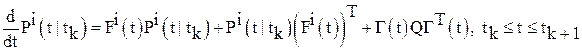 ; (8)
; (8)
![]() ; (9)
; (9)
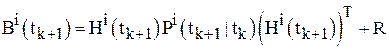 ; (10)
; (10)
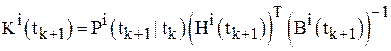 ; (11)
; (11)
![]() ; (12)
; (12)
![]() (13)
(13)
с начальными условиями , для ![]() ,
, ![]() ,
, ![]() .
.
Задача (5) с целевой функцией (6) является задачей нелинейного программирования с ограничениями. Для ее решения воспользуемся методом последовательного квадратичного программирования [4], что предполагает необходимость разработки алгоритмов вычисления значений критериев идентификации и их градиентов.
Эквивалентная выражению (6) запись
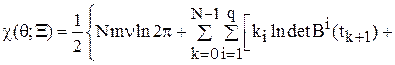
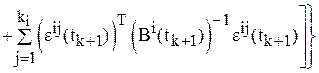 (14)
(14)
позволяет предложить следующие алгоритмы вычисления значения критерия максимального правдоподобия для линеаризованных моделей при некотором фиксированном ![]() .
.
Приведем для начала алгоритм вычисления значения критерия максимального правдоподобия для случая применения линеаризации во временной области:
Шаг 1. Определить ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Шаг 2. Положить ![]() ,
, ![]() =0,
=0, ![]() .
.
Шаг 3. Положить ![]() .
.
Шаг 4. Выбрать ![]() , если k=0.
, если k=0.
Шаг 5. Задать ![]() и, решив дифференциальное уравнение (ДУ)
и, решив дифференциальное уравнение (ДУ)
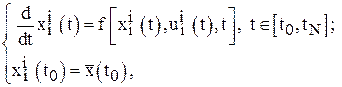
найти ![]() . Определить
. Определить ![]() и по формулам
и по формулам

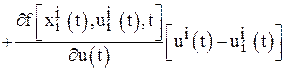 ; (15)
; (15)
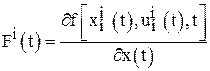 (16)
(16)
найти ![]() и
и ![]() для
для ![]() соответственно.
соответственно.
Шаг 6. Найти ![]() ,
,![]() по формулам
по формулам
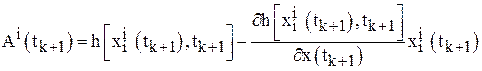 ; (17)
; (17)
 . (18)
. (18)
Шаг 7. Используя выражения (8), (10), (11), (13) вычислить ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Шаг 8. Вычислить ![]() . Положить j=1.
. Положить j=1.
Шаг 9. Если ![]() , выбрать
, выбрать ![]() .
.
Шаг 10. Используя выражения (7), (9), (12) вычислить ![]() ,
, ![]() ,
, ![]() .
.
Шаг 11. Вычислить 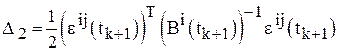 .
.
Шаг 12. Положить ![]() .
.
Шаг 13. Увеличить ![]() на единицу. Если
на единицу. Если ![]() , перейти на шаг 9.
, перейти на шаг 9.
Шаг 14. Увеличить ![]() на единицу. Если
на единицу. Если ![]() , перейти на шаг 4.
, перейти на шаг 4.
Шаг 15. Увеличить ![]() на единицу. Если
на единицу. Если ![]() , перейти на шаг 3.
, перейти на шаг 3.
Шаг 16. Положить ![]() и закончить процесс.
и закончить процесс.
Большинство шагов алгоритма вычисления значения критерия максимального правдоподобия в случае применения статистической линеаризации совпадут с соответствующими шагами алгоритма, описанного выше. Уточним, какие именно шаги требуют корректировки, не повторяя шаги, оставшиеся без изменений:
Шаг 5. Определить ![]() и, решив системы ДУ
и, решив системы ДУ


найти ![]() и
и ![]() . По формулам
. По формулам
![]()
![]() ; (19)
; (19)
![]() , (20)
, (20)
в которых
![]()
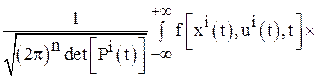
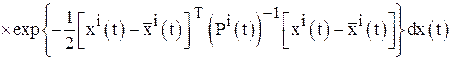 ;
;
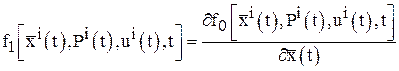 ,
,
найти ![]() и
и ![]() для
для ![]() соответственно.
соответственно.
Шаг 6. Найти ![]() ,
,![]() по формулам
по формулам
![]()
![]() ; (21)
; (21)
![]()
![]() , (22)
, (22)
где
![]()

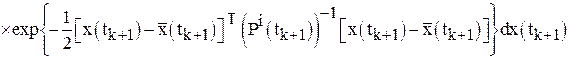 ;
;
 .
.
Продифференцировав равенство (14) по ![]() , получим
, получим
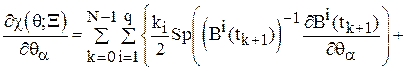
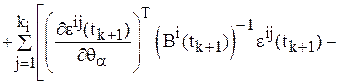
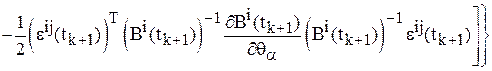 ,
,
что позволяет предложить следующие алгоритмы вычисления градиента критерия максимального правдоподобия для линеаризованных моделей при некотором фиксированном ![]() .
.
Приведем для начала алгоритм вычисления градиента критерия максимального правдоподобия для случая применения линеаризации во временной области:
Шаг 1. Определить ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,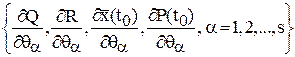 ,
, ![]() ,
, 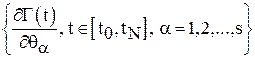 .
.
Шаг 2. Положить  ,
, ![]() ,
, ![]() .
.
Шаг 3. Положить ![]() .
.
Шаг 4. Если ![]() , выбрать
, выбрать ![]() ,
, 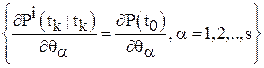 .
.
Шаг 5. Задать ![]() и, решив дифференциальное уравнение (ДУ)
и, решив дифференциальное уравнение (ДУ)

найти ![]() и
и 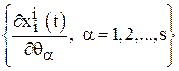 . Определить
. Определить ![]() и по формуле (15) найти
и по формуле (15) найти ![]() и
и  для
для ![]() . Используя выражение (16), получить
. Используя выражение (16), получить ![]() и
и  для
для ![]() .
.
Шаг 6. При помощи равенств (17), (18) найти ![]() , и
, и ![]() ,
, 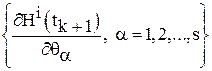 соответственно.
соответственно.
Шаг 7. Используя соотношения (8), (10), (11), (13) вычислить ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Шаг 8. Найти 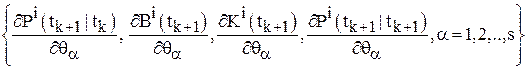 по формулам, вытекающим из уравнений (8), (10), (11), (13):
по формулам, вытекающим из уравнений (8), (10), (11), (13):
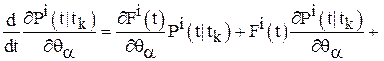
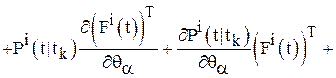
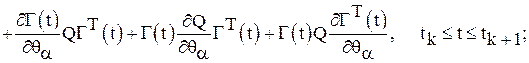
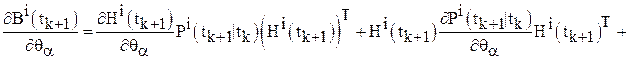
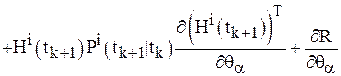 ;
;
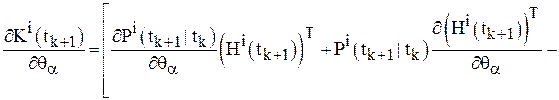
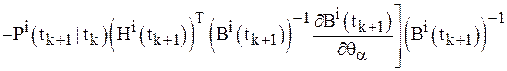 ;
;
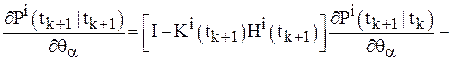
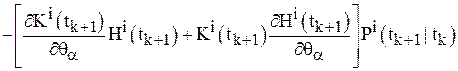 .
.
Шаг 9. Вычислить
 ,
, ![]() .
.
Положить ![]() .
.
Шаг 10. Если ![]() ,
, ![]() ,
, 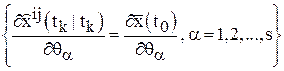 .
.
Шаг 11. Используя выражения (7), (9), (12), вычислить ![]() ,
, ![]() ,
, ![]() .
.
Шаг 12. Найти  по формулам, вытекающим из уравнений (7), (9), (12):
по формулам, вытекающим из уравнений (7), (9), (12):
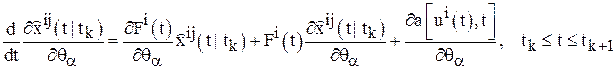 ;
;
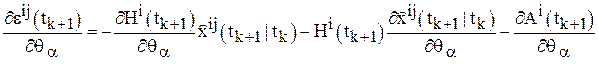 ;
;
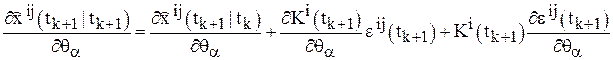 .
.
Шаг 13. Вычислить
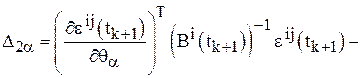
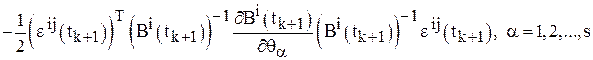 .
.
Шаг 14. Положить 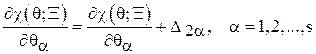 .
.
Шаг 15. Увеличить ![]() на единицу. Если
на единицу. Если ![]() , перейти на шаг 10.
, перейти на шаг 10.
Шаг 16. Увеличить ![]() на единицу. Если
на единицу. Если ![]() , перейти на шаг 4.
, перейти на шаг 4.
Шаг 17. Увеличить ![]() на единицу. Если
на единицу. Если ![]() , перейти на шаг 3.
, перейти на шаг 3.
Шаг 18. Положить 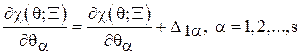 и закончить процесс.
и закончить процесс.
Большинство шагов алгоритма вычисления градиента критерия максимального правдоподобия в случае применения статистической линеаризации совпадут с соответствующими шагами алгоритма, описанного выше. Уточним, какие именно шаги требуют корректировки, не повторяя шаги, оставшиеся без изменений:
Шаг 5. Определить ![]() и, решив системы ДУ
и, решив системы ДУ
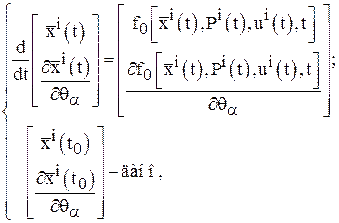
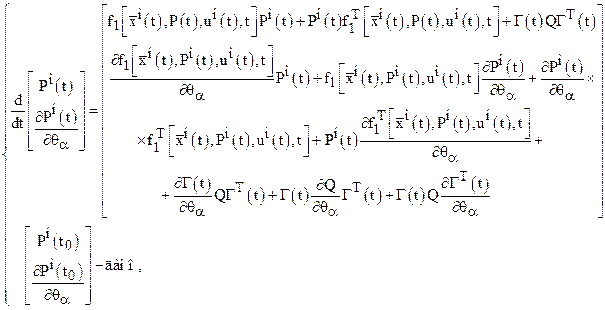
найти ![]() ,
, ![]() ,
, 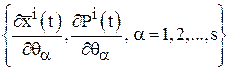 . По формуле (19), найти
. По формуле (19), найти ![]() и
и  для
для ![]() . Используя выражение (20), получить
. Используя выражение (20), получить ![]() и
и 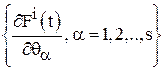 для
для ![]() .
.
Шаг 6. При помощи равенств (21), (22) найти ![]() , и
, и ![]() ,
, 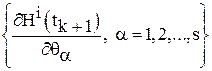 соответственно.
соответственно.
Данные вычислительные алгоритмы были программно реализованы в рамках интерактивной программной системы активной параметрической идентификации стохастических динамических систем (APIS 1.0) [7].
Для линейных нестационарных моделей вида (3), (4) алгоритмы вычисления значения критерия максимального правдоподобия и его градиента имеют похожие структуры с алгоритмами, представленными выше, но являются более простыми в силу отсутствия в формулах (6)-(13) зависимости от индекса i в матрицах ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и векторе
и векторе ![]() . Матрицы и вектора, входящие в модель (3), (4), определяются по формулам, записанным в самой модели и не требуют дополнительных расчетов.
. Матрицы и вектора, входящие в модель (3), (4), определяются по формулам, записанным в самой модели и не требуют дополнительных расчетов.
Список литературы:
- Денисов В.И., Чубич В.М., Филиппова Е.В. Активная параметрическая идентификация стохастических непрерывно-дискретных систем, полученных в результате применения статистической линеаризации // Сибирский журнал индустриальной математики. — 2012. — Т. XV. — № 4(52). — С. 78—89.
- Денисов В.И., Чубич В.М., Черникова О.С., Бобылева Д.И. Активная параметрическая идентификация стохастических линейных систем: монография. Новосибирск: Изд-во НГТУ, 2009. — 192 с.
- Ивченко Г.И., Медведев Ю.И. Введение в математическую статистику. М.: Изд-во ЛКИ, 2010. — 600 с.
- Измаилов А.Ф., Солодов М.В. Численные методы оптимизации. М.: ФИЗМАТЛИТ, 2008. — 320 с.
- Огарков М.А. Методы статистического оценивания параметров случайных процессов. М.: Энергоатомиздат, 1980. — 208 c.
- Чубич В.М., Филиппова Е.В. Применение методов теории планирования экспериментов при параметрической идентификации стохастических нелинейных непрерывно-дискретных систем // АПЭП 2010. Актуальные проблемы электронного приборостроения: материалы X Международной конф. — Новосибирск. — 2010. — Т. 6. — С. 85—93.
- Чубич В.М., Черникова О.С., Филиппова Е.В. Интерактивная программная система активной параметрической идентификации стохастических динамических систем (APIS 1.0) // Свидетельство о государственной регистрации программы для ЭВМ №2012617399. — М.: Роспатент. — 2012.
- Áström K. Maximum likelihood and prediction errors methods // Automatica, 1980. V. 16. pp. 551—574.
- Gupta N., Mehra R. Computational aspects of maximum likelihood estimation and reduction in sensitivity function calculations // IEEE Trans. Automat. Control. — 1974. — V. 19 — № 6. — P. 774—783.
дипломов


Оставить комментарий