Статья опубликована в рамках: XXI Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 15 мая 2013 г.)
Наука: Технические науки
Секция: Аэрокосмическая техника и технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
КОМПЛЕКСНЫЙ ПОДХОД В СОВЕРШЕНСТВОВАНИИ СОЗДАНИЯ ИНТЕГРАЛЬНЫХ АВИАКОНСТРУКЦИЙ ИЗ ПОЛИМЕРНЫХ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ С ТРУБЧАТЫМ ЗАПОЛНИТЕЛЕМ
Майорова Екатерина Владимировна
аспирантка Национального аэрокосмического университета им. Н.Е. Жуковского «ХАИ», г. Харьков
INTEGRATED APPROACH IN IMPROVEMENT OF CREATION OF INTEGRATED AVIADESIGNS FROM POLYMERIC COMPOSITE MATERIALS WITH TUBULAR FILLER
Majorova Ekaterina
The graduate student of National Aerospace University named after N E. Zhukovsky "KhAI", Kharkov
АННОТАЦИЯ
Рассмотрены вопросы совершенствования создания малогабаритных трубчатых интегральных авиаконструкций из полимерных композиционных материалов (ПКМ) на основе комплексного подхода к их проектированию с обеспечением регламентированного уровня качества и ресурса.
В основе комплексного подхода лежит методика предэскизного проектирования панельных конструкций летательных аппаратов с трубчатым заполнителем и синтез физико-механических и прочностных характеристик трубчатого заполнителя трехслойных конструкций.
ABSTRACT
Questions of improvement of creation of small-sized tubular integrated aviadesigns from the polymeric composite materials (PCM) on the basis of an integrated approach to their design with providing the regulated level of quality and a resource are considered.
At the heart of an integrated approach the technique of preoutline design of panel designs of aircraft with tubular filler and synthesis of physicomechanical and strength characteristics of tubular filler of three-layer designs lies.
Ключевые слова: интегральные авиаконструкции из ПКМ; трубчатый заполнитель; метод синтеза.
Keywords: integrated aircraft-designs from PСM; tubular filler; a synthesis method.
История развития самолетостроения показывает, что существенного изменения эффективности летательного аппарата можно достичь, только создавая новые конструкции, использующие новые технические возможности и новые материалы, причем, выбор материала для конструкции может предопределить основные ее характеристики [4]. В последние 40 лет усилия исследователей и практиков во всем мире были направлены на внедрение в авиастроение принципиально новых материалов, состоящих из высокопрочных и жестких волокон, соединенных между собой полимерным связующим, и получивших название полимерных композиционные материалы [4—5].
Одним из прогрессивным направлений внедрения ПКМ с целью повышения эффективности агрегатов летательных аппаратов считается создание трехслойных конструкций. Из накопленного отечественного и зарубежного опыта [7] можно выделить сотовые конструкции. Однако для различных функций и условий работы они не могут рассматриваться как единственно возможными и приемлемыми. Преимущества сотовых заполнителей (СЗ) общеизвестны [2, 4—5, 7]. К их недостаткам, проявляющимся особенно в панелях планера самолета, в первую очередь, относится накопление влаги в полости СЗ. В связи с этим вместо СЗ с конца 60-х годов прошлого столетия стали применять трубчатый заполнитель (ТЗ) [7].
Однако, если физико-механические характеристики (ФМХ) СЗ с конца 50-х годов рассчитываются аналитически по формулам А.Я. Александрова [1], то ФМХ и прочностные свойства ТЗ отсутствуют, а несущая способность панельных и оболочечных конструкций на их основе, устанавливается преимущественно экспериментально.
Представим комплексный подход к проектированию ТЗ в классе рассматриваемых малогабаритных трубчатых конструкций типа небольших панелей, триммеров и элеронов из ПКМ интегральной схемы (рис. 1).

Рисунок 1. Фрагмент интегральной авиаконструкции из ПКМ с ТЗ
Первым этапом при создании конструкции с ТЗ является ее предэскизное проектирование, которое позволит получить оптимальную ориентацию трубчатых элементов в панеле или оболочке, их количестве, геометрических параметров конкретного ПКМ при заданных нагрузках. Точные расчетные схемы (РС) панельных конструкций с дискретными закреплениями для их проектирования практически отсутствуют. В связи с этим на практике конструкторы всегда использовали и продолжают использовать для эскизного проектирования таких агрегатов интуитивно выбираемые приближенные РС в виде различного рода стержневых (балочных) систем, в последующем расчленяемых на отдельные балки.
После выбора квазиоптимальных геометрических параметров таких стержней, обеспечивающих их несущую способность при заданных нагрузках при минимальной массе, следующим этапом будет поверочный расчет исходной панельной конструкции методом конечных элементов (МКЭ) с последующей корректировкой геометрии сечений при обнаружении локальных зон, в которых не обеспечена прочность или жесткость.
В качестве примера на рисунке 2 показана прямоугольная в плане панель с шомпольным шарнирным соединением вдоль оси Х и двумя дискретными шарнирными опорами, нагруженная равномерной распределенной поперечной нагрузкой ![]() .
.
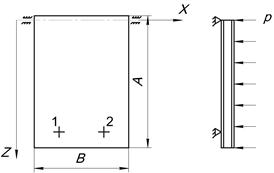
Рисунок 2. Исходная панель: 1, 2 — дискретные шарнирные опоры
Панель имеет трехслойную структуру с заполнителем в виде трубок, ориентированных по одному из направлений Х или Z. Перераспределение внешней поверхностной нагрузки ![]() будем осуществлять исходя из постоянной для всех балок системы ширины а, которая определяется из равенства площади поверхности панели площади поверхности всех заменяющих балок, т. е.
будем осуществлять исходя из постоянной для всех балок системы ширины а, которая определяется из равенства площади поверхности панели площади поверхности всех заменяющих балок, т. е.
![]() , (1)
, (1)
где: ![]() — число балок в направлении оси
— число балок в направлении оси ![]() ;
;
![]() — число балок в направлении оси
— число балок в направлении оси ![]() .
.
Решая уравнение (1) относительно а, получим
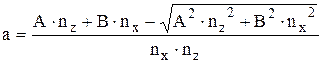 . (2)
. (2)
Погонное усилие на каждую балку ![]() определится как произведение поверхностной нагрузи
определится как произведение поверхностной нагрузи ![]() на ширину
на ширину ![]() :
:
![]() . (3)
. (3)
Далее необходимо рассматривать выделенные в той или иной РС балки под действием погонной нагрузки ![]() .
.
Для демонстрации предлагаемой методики предэскизного проектирования панели остановимся на РС, показанной на рис. 3, в которой выделяется всего три балки двух типов: две в направлении оси Z (![]() 2) — балки первого типа (рис. 4), и одна – в направлении оси X (
2) — балки первого типа (рис. 4), и одна – в направлении оси X (![]() 1) – балки второго типа (рис. 5).
1) – балки второго типа (рис. 5).
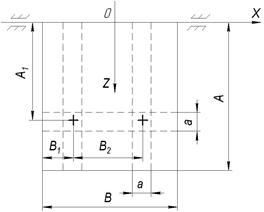
Рисунок 3. Подкласс рассматриваемой панели

Рисунок 4. Балка первого типа

Рисунок 5. Балка второго типа

Рисунок 6. Эпюры перерезывающих сил и изгибающих моментов в балке второго типа
Из рис. 4 и 5 видно, что балка первого типа является частным случаем балки второго типа, к которому приходим при ![]() . Поэтому для определения действующих на балку изгибающих моментов М и перерезывающих сил Q рассмотрим балку второго типа, введя обозначение выделенных участков
. Поэтому для определения действующих на балку изгибающих моментов М и перерезывающих сил Q рассмотрим балку второго типа, введя обозначение выделенных участков ![]() ,
, ![]() и
и ![]() . Эпюры перерезывающих сил Q и изгибающих моментов М от действия погонной нагрузки
. Эпюры перерезывающих сил Q и изгибающих моментов М от действия погонной нагрузки ![]() на каждую балку показаны на рис. 6.
на каждую балку показаны на рис. 6.
Тогда реакции ![]() и
и ![]() в опорах А и В соответственно будут иметь вид:
в опорах А и В соответственно будут иметь вид:
 (4)
(4)
Перерезывающие силы Q и изгибающие моменты М на участках балки 1, 2 и 3:
![]() при 0
при 0![]() x<c;
x<c;
![]() при с
при с![]() x<(c+l);
x<(c+l);
![]() при (с+l)
при (с+l)![]() x
x![]() (c+l+b);
(c+l+b);
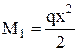 при 0
при 0![]() x<c; (5)
x<c; (5)
 при с
при с![]() x<(c+l);
x<(c+l);
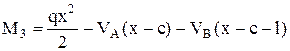 при (с+l)
при (с+l)![]() x
x![]() (c+l+b).
(c+l+b).
Соответствующие этим участкам прогибы ![]() ,
, ![]() ,
, ![]() наиболее просто определяются с помощью теоремы Кастильно [1]:
наиболее просто определяются с помощью теоремы Кастильно [1]:
(6)
Для ограничения изгибной жесткости панели следует принять неравенство
, (7)
где: верхние индексы (1) и (2) обозначают тип балки (и далее по тексту);
![]() — допустимое значение прогиба панели, м.
— допустимое значение прогиба панели, м.
Максимальные напряжения в балках первого и второго типов определяются по известным формулам сопротивления материала:
 (8)
(8)
где: ![]() — максимальный предел прочности балки при растяжении (сжатии), МПа;
— максимальный предел прочности балки при растяжении (сжатии), МПа;
![]() — максимальный изгибный момент на участке балки, Н∙м;
— максимальный изгибный момент на участке балки, Н∙м;
W — момент сопротивления балки, м3 ;
![]() — максимальный предел прочности участка балки при изгибе, МПа;
— максимальный предел прочности участка балки при изгибе, МПа;
![]() — максимальное перерезывающее усилие на участке балки, Н/м2 ;
— максимальное перерезывающее усилие на участке балки, Н/м2 ;
![]() — площадь сдвига балок, м2 ;
— площадь сдвига балок, м2 ;
![]() ,
, ![]() ,
, ![]() — изгибающие моменты в опоре А, на втором участке l, в опоре В балки соответственно, Н∙м.
— изгибающие моменты в опоре А, на втором участке l, в опоре В балки соответственно, Н∙м.
Величина момента инерции сечения балки будет различной в зависимости от направления оси ТЗ. Так для балок первого и второго типов:
· при ориентации ТЗ вдоль оси Z
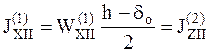 ; (9)
; (9)
· при ориентации ТЗ поперек оси Z
 ; (10)
; (10)
где: ![]() ,
, ![]() — момент сопротивления балки первого типа при ориентации ТЗ вдоль оси Х и поперек оси Х соответственно, м3;
— момент сопротивления балки первого типа при ориентации ТЗ вдоль оси Х и поперек оси Х соответственно, м3;
h — высота трубчатого заполнителя, м;
![]() — толщина обшивки в панеле, м.
— толщина обшивки в панеле, м.
Аналогичная картина и с моментами сопротивления двух балок:
 (11)
(11)
Определяем площади сдвига для балки первого и второго типов:
· при ориентации ТЗ вдоль оси Z
 , (12)
, (12)
где: ![]() — толщина трубчатого заполнителя, м;
— толщина трубчатого заполнителя, м;
![]() — число трубок в ширине балки а.
— число трубок в ширине балки а.
· при ориентации ТЗ вдоль оси Х принято, что на сдвиг работают только удвоенная толщина ТЗ на шаге t . Тогда для балки первого типа
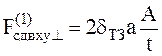 , (13)
, (13)
где: ![]() — площадь сдвига, приходящаяся на шаг t ТЗ, м2;
— площадь сдвига, приходящаяся на шаг t ТЗ, м2;
![]() — количество площадей сдвига, приходящихся на длину балки А.
— количество площадей сдвига, приходящихся на длину балки А.
Соответственно площадь сдвига для балки второго типа при ориентации ТЗ вдоль оси X:
 , (14)
, (14)
где: ![]() — количество площадей сдвига, приходящихся на длину балки В.
— количество площадей сдвига, приходящихся на длину балки В.
Прочность соответствующих балок на сдвиг следует определять по критерию
 . (15)
. (15)
Далее необходимо сделать выбор проектных параметров панели по следующему алгоритму. Сначала полагаем, что ТЗ ориентирован вдоль оси Z. Запишем
 , (16)
, (16)
где: ![]() — предел прочности ПКМ обшивки в направлении оси Z.
— предел прочности ПКМ обшивки в направлении оси Z.
Из формулы (11) следует, что ![]() является функцией параметров:
является функцией параметров:
![]() , (17)
, (17)
где индексы II означают, что соответствующие параметры выбраны при ориентации ТЗ вдоль оси Z. Исходя из (17) неравенство (11) можно записать как
![]() . (18)
. (18)
Аналогично с учетом того, что
![]() (19)
(19)
и параметры ![]() и
и ![]() определяются формулами (12) и (14) соответственно, а максимальный прогиб fmax зависит от параметров
определяются формулами (12) и (14) соответственно, а максимальный прогиб fmax зависит от параметров ![]() , можно записать
, можно записать
(20)
При ориентации ТЗ по оси Х выражения (20) лишь поменяются местами.
В качестве дополнительных условий для анализа возможности разрешения системы неравенств (16)—(20) можно добавить следующие:
1. Одно из первых двух неравенств системы (20) может быть обращено в равенство. Очевидно, это должно быть то из них, в котором действующее напряжение больше. По-видимому, это ![]() , так как момент сопротивления
, так как момент сопротивления ![]() , из чего следует, что
, из чего следует, что ![]() может быть принято равным
может быть принято равным ![]() .
.
2. ТЗ обычно формируют на оправках намоткой полуфабриката ПКМ из однонаправленной ленты под углами ![]() . Обычно для ТЗ достаточно одной пары монослоев. Таким образом, толщина ТЗ и его модуль упругости Етр в первом приближении оказываются известными.
. Обычно для ТЗ достаточно одной пары монослоев. Таким образом, толщина ТЗ и его модуль упругости Етр в первом приближении оказываются известными.
3. Максимальная перерезывающая сила в балке второго типа априори больше, чем в балке первого типа. Тогда имеется основание неравенство для ![]() системы (20) заменить равенством:
системы (20) заменить равенством: ![]() .
.
4. Пределы прочности ПКМ и его модули упругости зависят от схемы армирования. Как правило схема армирования из монослоев ПКМ имеет вид
5.
![]() , (21)
, (21)
где: m, n, l — число монослоев, ориентированных в соответствующем направлении (![]() – рассматривается как один монослой двойной толщины);
– рассматривается как один монослой двойной толщины);
s — число кратности слоев данной структуры.
Для панели, нагруженной поперечной равномерной нагрузкой представляется оправданным в первом приближении принять схему армирования с параметрами: m=l=1, n=1, s=1.
Тогда согласно [7] можно принять
 ;
;
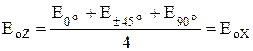 ;
;
 ; (22)
; (22)
 .
.
При допущениях п. 3 получим
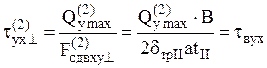 . (23)
. (23)
Откуда
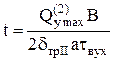 . (24)
. (24)
1. Первое равенство системы (20) запишем как
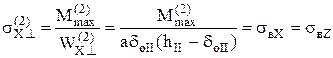 . (25)
. (25)
Откуда
 . (26)
. (26)
2. Рассмотрев неравенство (18) в развернутом виде, запишем
![]()
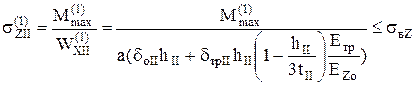 , (27)
, (27)
где все параметры известны, следует проверить только его выполнение.
В случае невыполнения (27) в первую очередь следует осуществить его коррекцию, увеличивая ![]() . При увеличенном
. При увеличенном ![]() первое неравенство системы (18) будет выполняться именно в этом статусе, а не в виде неравенства, как было принято выше.
первое неравенство системы (18) будет выполняться именно в этом статусе, а не в виде неравенства, как было принято выше.
3. Остается проверить последнее неравенство:
![]() , (28)
, (28)
где максимальные прогибы балок первого и второго типов могут быть эффективно и наиболее просто уменьшены в случае его нарушения за счет увеличения момента инерции, что в первую очередь возможно увеличением ![]() . После установления неизвестных, удовлетворяющих неравенствам (18)—(20), необходимо определить массу панели
. После установления неизвестных, удовлетворяющих неравенствам (18)—(20), необходимо определить массу панели
 . (29)
. (29)
После этого проводится выбор проектных параметров по приведенному выше алгоритму при ориентации ТЗ вдоль оси Х панели и определяется ее масса
 . (30)
. (30)
Весовую эффективность панели можно определить соотношением
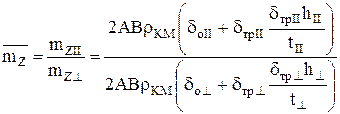 . (31)
. (31)
Отметим, что выше рассматривалась демонстрация предложенной методики выбора конструктивных параметров конкретной панельной конструкции (рис. 1). Естественно, при выборе другого подкласса панели общность методики выразится только в каноничности формул (1)—(3) тогда, как все последующие формулы изменяются, и алгоритм предэскизного проектирования панельных конструкций из ПКМ с ТЗ сохраняет общность.
Дальнейшая проверка результатов предэскизного проектирования панельных конструкций из ПКМ должна проводиться в пакете МКЭ. Однако оптимальное проектирование и поверочный расчет таких конструкций в пакете МКЭ требуют использования ФМХ ТЗ, в которых трубки заменены некоторым сплошным ортотропным материалом («размазаны»).
В таблице 1 представлены формулы для определения ФМХ ТЗ, определенных по методике, аналогичной реализованной в [4] для СЗ. Она состоит в реализации требования равенства относительных деформаций условного сплошного типового элемента и реального, выделенного в пределах одной трубки, учитывающего только ее материал. Приведенные ФМХ ТЗ необходимы для определения напряженно-деформированного состояния в соответствующем слое сложной панели при заданных внешних нагрузках.
Таблица 1.
Физико-механические характеристики ТЗ
|
Характеристика |
Формула |
|
Модуль упругости вдоль оси Z при растяжении (сжатии) |
|
|
Модуль упругости вдоль оси X при растяжении (сжатии) |
|
|
Модуль упругости вдоль оси Y при растяжении (сжатии) |
|
|
Модуль сдвига в плоскости XОY |
|
|
Модуль сдвига в плоскости YОZ |
|
|
Модуль сдвига в плоскости XОZ |
|
|
Коэффициент Пуассона при сжатии по оси Х при растяжении по оси Z |
|
|
Коэффициент Пуассона при сжатии по оси Z при растяжении по оси Х |
|
|
Коэффициент Пуассона при сжатии по оси Y при растяжении по оси Z |
|
|
Коэффициент Пуассона при сжатии по оси Z при растяжении по оси Y |
|
|
Коэффициент Пуассона при сжатии по оси X при растяжении по оси Y |
|
|
Коэффициент Пуассона при сжатии по оси Y при растяжении по оси X |
|
где: «+» и «-» — растяжение и сжатие соответственно в направлении осей X, Y и Z;
«км» — композитный материал трубчатого элемента.
В таблице 2 представлены формулы для определения приведенных характеристик пределов прочности ТЗ из ПКМ при растяжении, сжатии и сдвиге [6] для проверки прочности заполнителя по принятому критерию прочности.
Таблица 2.
Приведенные характеристики пределов прочности ТЗ
|
Характеристика |
Формула |
|
Приведенный предел прочности ТЗ в направлении оси Z |
|
|
Приведенный предел прочности ТЗ в направлении оси Z |
|
|
Приведенный предел прочности ТЗ в направлении оси X |
|
|
Приведенный предел прочности ТЗ в направлении оси X |
|
|
Приведенный предел прочности ТЗ в направлении оси Y |
|
|
Приведенный предел прочности ТЗ в направлении оси Y |
|
|
Предел прочности при сдвиге в плоскости YOZ |
|
где: индексы «кр» — критическое значение параметра;
«тр» — трубка;
«кл» — клей.
Таким образом, в основе комплексного подхода проектирования ТЗ из ПКМ рассматриваемого класса является предэскизное проектирование панельных трехслойных конструкций летательных аппаратов и синтез физико-механических и прочностных характеристик, что позволит установить геометрические параметры обшивки и ТЗ, определить эффективную по массе ориентации трубок в панели, а также произвести расчеты на прочность и устойчивость по отработанным методикам, используемых для сэндвичевых сотовых агрегатов как в аналитическом виде, так и в МКЭ.
Список литературы:
1.Беляев Н.М. Сопротивление материалов / Н.М. Беляев. — М.: Наука, 1976. — 607 с.
2.Вигдорчик С.А. Технологические основы проектирования и конструирования самолетов: конспект лекций. — МАИ, 1978. — 139 с.
3.Вопросы расчета элементов авиационных конструкций. Расчет трехслойных панелей и оболочек: сб. статей / под ред. А.Я. Александрова. — Вып. 2. — М.: Оборонгиз, 1969. — 146 с.
4.Востин Луис Ф. Агрегаты из композиционных материалов для гражданских транспортных самолетов: пер. с англ. № 2245. ЦНТИ «Волна». — Киев, 1978. — 41 с.
5.Применение конструкционных пластмасс в производстве летательных аппаратов: учеб. / под ред. А.Л. Абибова. — М.: Машиностроение, 1971. — 192 с.
6.Расчеты элементов авиационных конструкций: сб. статей / под ред. А.Я. Александрова, Э.И. Григолюка и Л.М. Куршина. — М.: Машиностроение, 1965. — Вып. 3. — 274 с.
7.Технология производства изделий интегральных конструкций из композиционных материалов в машиностроении: учеб. / науч. ред. А.Г. Братухин, В.С. Боголюбов, О.С. Сироткин. — М.: Готика, 2003. — 516 с.
дипломов





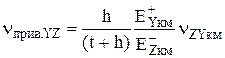
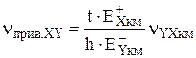
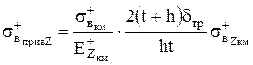



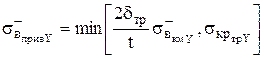

Оставить комментарий