ИССЛЕДОВИНИЕ  РЕЗОНАНСНЫХ  ЯВЛЕНИЙ  В  ДИНАМИЧЕСКИХ  ПРОЦЕССАХ  ВИБРОСЕПАРАЦИИ  СЫПУЧИХ  СРЕД

Ребот  Дарья  Петровна

ассистент  НУ  «Львовская  политехника»,  Львов

E-mail:  dasha_kotlyarova@ukr.net

Стоцько  Зиновий  Антонович

д-р  техн.  наук,  професор  НУ  «Львовская  политехника»,  Львов

E-mail:  stotsko@polynet.lviv.ua

Топильницкий  Владимир  Григорьевич

канд.  техн.  наук,  доцент  НУ  «Львовская  политехника»,  Львов

E-mail:  topilnvol@mail.ru

INVESTIGATION  OF  RESONANCE  PHENOMENA  IN  DYNAMIC  PROCESSES  IN  VIBRATORY  SEPARATORS  OF  GRANULAR  MEDIA

Rebot  Daria  Petrovna

Assistant  of  the  "Lviv  Polytechnic"  NU,  Lviv

Stotsko  Zinovij  Antonovich

Ph.D.,  professor  of  the  "Lviv  Polytechnic"  NU,  Lviv

Topilnytskyy  Wladimir  Grigorjevich

C.T.S.,  Associate  Professor  of  the  "Lviv  Polytechnic"  NU,  Lviv

АННОТАЦИЯ

Для  сильно  нелинейных  моделей  описания  динамики  сыпучей  среды  получено  соотношение,  определяющее  амплитуду  резонанса.  Описана  динамика  сыпучей  среды  в  границах  указанного  значения  амплитуды.  Полученные  результаты  позволят  в  дальнейшем  повысить  эффективность  вибросепарации.

ABSTRACT

For  strongly  nonlinear  dynamics  models  of  loose  medium  the  ratio,  which  determines  the  amplitude  of  the  resonance  is  obtained.  The  dynamics  of  loose  environment  in  the  vicinity  of  the  specified  amplitude  is  described.  The  results  obtained  in  investigation  subsequently  allow  to  increasing  the  efficiency  of  the  vibratory  separation.

Ключевые  слова:  сыпучая  среда;  резонанс;  амплитуда;  колебания;  динамический.

Keywords:  loose  medium;  resonance;  amplitude;  оoscillations;  dynamic.

Вибросепарация  сыпучей  среды  является  важным  технологическим  процессом  в  промышленности  и  требует  дополнительных  исследований.  Движение  сыпучей  среды  в  вибрационных  сепараторах  рассматривались  на  основе  многих  гипотез,  однако,  ни  одна  из  них  не  описывает  в  полном  объеме  характер  процесса,  а  только  в  определенных  узких  пределах.  Учитывая,  что  этот  вопрос  является  достаточно  объемным,  он  продолжает  оставаться  открытым  и  требует  более  глубокого  исследования  с  учетом  типа  и  характеристик  вибрационной  машины  (сепаратора),  а  также  обрабатываемой  среды.  Поэтому  в  работе  с  единой  позиции  рассмотрена  динамика  сыпучей  среды  в  вибрационном  сепараторе,  которая  моделируется  как  наслоение  плоских  упруго-пластических  балок.  Такой  подход  в  исследовании  динамики  среды  рассматривался  при  исследовании  установок  вибрационной  объемной  обработки  деталей  [1,  с.  26;  2,  с.  6].  Однако  вибросепарация  имеет  принципиальные  отличия  от  вибрационной  обработки.  Основным  из  них  является  тот  факт,  что  в  исследуемом  случае  среда  движется  вдоль  сита.  Поэтому  этот  случай  требует  определения  амплитудно-частотных  характеристик  сыпучей  среды  с  учетом  ее  движения  вдоль  сита. 

Как  известно  производительность  и  интенсивность  сепарации  зависит  от  воздействия  широкого  спектра  внешних  и  внутренних  факторов  на  этот  процесс  [4,  c.  22].  Вследствие  этого  происходит  сложное  взаимодействие  между  частицами  материала  что  сепарируется,  изменение  динамических  характеристик  последнего.  Это  взаимодействие  требует  длительного  и  сложного  изучения  и  не  полностью  исследовано.  Поэтому  важной  задачей  является  необходимость  более  глубокого  рассмотрения  динамического  процесса  вибрационной  сепарации.  Этот  вопрос  является  предметом  изучения  в  данной  работе.

Рассмотрим  схему  вибрационного  сепаратора  с  несколькими  ситами,  которые  находятся  под  определенным  углом  к  горизонту,  корпус  сепаратора  совершает  возвратно  -  поступательное  горизонтальное  движение.

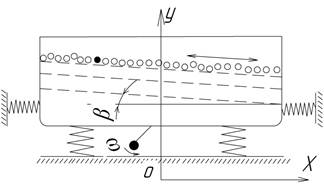
Рисунок  1.  Расчетная  схема  вибрационного  сепаратора

Будем  считать,  что  сыпучая  среда  рассматривается  как  наслоение  плоских  упруго-пластических  балок.  Учитывая,  что  она  движется  вдоль  сита  с  определенной  скоростью,  дифференциальное  уравнение  движения  сыпучей  среды  можно  записать  [3,  с.  127]:

,              (1)

где: 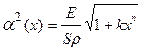   —  медленно  переменная  функція,  учитывающая  изменение  физико-механических  характеристик  сыпучей  среды  вдоль  сита  [3,  с.  127]; 

  —  плотность  среды; 

—  площадь  поперечного  сечения  элементарного  слоя  сыпучей  среды; 

—  координата  произвольного  поперечного  сечения  слоя  сыпучей  среды; 

—  перемещение  произвольного  поперечного  сечения  сыпучей  среды  вдоль  оси  ;

;    —  относительная  деформация  и  ускорение  слоя  сыпучей  среды; 

—  скорость  перемещения  слоя  сыпучей  среды; 

  —  «условный»  модуль  упругости  сыпучей  среды, 

—  некоторая  функция,  описывающая  нелинейные  и  периодические  силы  среды, 

—  малый  параметр.

Для  уравнения  (1)  будем  рассматривать  однородные  краевые  условия:

  (2)

Одночастотные  продольные  колебания  сыпучей  среды  в  процессе  вибросепарации,  на  горизонтально  расположенном  сите  описываются  зависимостью:

  (3)

Рассмотрим  только  случай  резонанса  на  частоте,  которая  кратная  частоте  внешнего  периодического  возмущения,  т.е.  .  Здесь  —  действительный  корень  уравнения  .  Так  что,  при  изменении  амплитуды  колебаний  в  малой  окрестности    с  точностью  до  величин  высшего  порядка  соотношение:

  (4)

К  тому  же,  в  резонансном  случае,  амплитуда  и  частота  колебаний  связаны  с  фазой  внешних  сил.  Учитывая  последнее,  при  определении  дифференциальных  уравнений  введем  в  систему  «разность  фаз»  —  .  Уравнение  для  амплитуды  и  фазы  динамического  процесса  запишем  как:

    (5)

Дифференциальные  уравнения  (5)  описывают  резонансные  колебания  сыпучей  среды,  поэтому  при  численном  их  интегрировании  за  начальное  значение  параметра    нужно  принимать  близко  .

Ниже  на  рис.  2.  представлены  зависимости  амплитуды  колебаний  сыпучей  среды,  при  которой  имеет  место  резонанс.

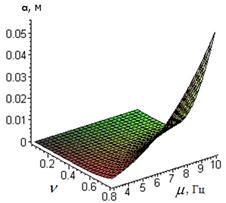
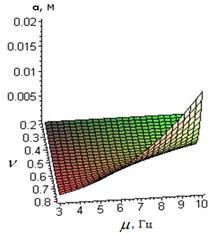
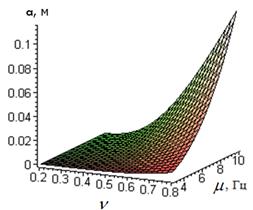
Рисунок  2.  Графики  зависимости  резонансной  амплитуды  от  параметра    и  частоты  колебания  сыпучей  среды.  а)    ;  б);  в)    г) 

Проанализировав  графики  можно  сделать  следующие  выводы:

·     если  амплитуда  колебаний  сыпучей  среды  является  меньше  значения  параметра  ,  то  резонансные  колебания  в  сыпучей  среде  не  будут  наблюдаться  при  условии  произвольной  частоты  горизонтальных  колебаний  контейнера;

·     если  же  амплитуда  колебаний  среды  вдоль  сита  является  больше  ,  то  силы  трения  постепенно  уменьшая  ее  к  значению  ,  вызывают  в  среде  резонансные  колебания,  а  значит  кратковременный  рост  амплитуды.  В  дальнейшем  процесс  повторяется.

Cписок  литературы:

1.Блехман  И.И.  О  теории  вибрационного  разделения  сыпучих  смесей  /  И.И.  Блехман,  В.Я.  Хайнман  //  Изв.  АН  СССР  Механика.  —  1965.  —  №  5.  —  с.  22—30.

2.Стоцько  З.А.  Динамика  рабочей  середы  вибрационных  машин  объемной  обработки  /  Стоцько  З.А.,  Сокил  Б.И.,  Топильницкий  В.Г  //  Укр.  межведомственный  научно-технический  сборник  Автоматизация  технологических  процессов  и  производств  в  машиностроении  и  приборостроении.  —  2000.  —  №  35.  —  с.  26—32.

3.Стоцько  З.А.  Динамика  сыпучей  среды  в  вибрационном  сепараторе  /  З.А.  Стоцько,  Б.И.  Сокіл,  Д.П.  Котлярова,  В.Г.  Топильницкий  //  Весник  НУЛП  Динамика,  мощность  и  проектирование  машин  и  приборов.  —  2008.  —  №  614.  —  с.  125—130.

4.Топильницкий  В.Г.  Динамические  процессы  в  вибромашинах  для  объемной  обработки  с  дебалансным  вибровозбудителем:  Автореф.  дис.  канд.техн.  наук.  —  Львов.  —  2002.  —  16  с.