Статья опубликована в рамках: XVI Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 12 декабря 2012 г.)
Наука: Технические науки
Секция: Приборостроение, метрология, радиотехника
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОСОБЕННОСТИ ЗОНДИРОВАНИЯ СВЕТОВОДА СЛОЖНОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Андросик Андрей Борисович
канд. техн. наук, доцент МГОУ, г. Москва
Мировицкая Светлана Дмитриевна
канд. техн. наук, доцент МГОУ, г. Москва
E-mail: scotchwood@yandex.ru
FEATURES OF SOUNDING THE FIBERS OF COMPLEX CROSS CECTION GEOMETRY
Andrey Androsik
Candidate of Technical Sciences, Associate Professor of MSOU, Moscow
Svetlana Mirovitskaya
Candidate of Technical Sciences, Associate Professor of MSOU, Moscow
АННОТАЦИЯ
В работе предложен модифицированный рефракционный метод исследования волоконных световодов сложного поперечного сечения на примере структуры в виде шестилепестковой розы. Даны результирующие формулы вычисления основных геометро-оптических характеристик световодов.
ABSTRACT
This work proposes a modified refraction method of investigation of optical fibers complex cross sections on the example of the structure in the form of six zone roses. The results of the formula of calculation of the main geometric and optical characteristics of optical fibers are given.
Ключевые слова: волоконный световод; рефракция; геометро-оптические характеристики.
Keywords: optical fiber; refraction; geometric and optical characteristics.
Изменения геометрических размеров сердцевины волоконного световода (ВС) по его длине существенно влияют на характеристики излучения, а небольшие отклонения диаметра оболочки (при достаточной ее толщине) не имеют большого значения для распространения излучения. Однако при изготовлении волоконно-оптических элементов (ВОЭ) — согласующих устройств, оптических соединителей, блоков, жгутов, пластин — внешние геометрические параметры весьма важны. Несоосность сердцевины и оболочки, их эллиптичность сильно влияют на параметры соединителей, фоконов, фокусирующих стержней. Требования к стабильности геометрических параметров ВС еще более возрастают для одномодовых волокон.
За последние время было разработано большее число бесконтактных оптических методов, базирующихся на различных оптических явлениях. К ним относятся интерференция и дифракция падающей на однородный или не однородный диэлектрический цилиндр плоской волны, рефракция узкого зондирующего пучка, излучение при прохождении пучка через диэлектрический цилиндр, его отражение от торца цилиндра и многие др. Методы контроля реализуются различными способами, использующими как интегральные преобразования (Фурье, Радона, Абеля), так и решения дифференциальных уравнений теории дифракции на диэлектрическом цилиндре [1, с. 36, 2, с. 54].
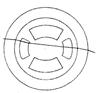
Ниже проанализированы особенности расчета волоконной структуры, содержащей оболочку и сердцевину с различными показателями преломления. Рассматривается волоконная структура с круглой оболочкой и сердечником в виде шести лепестковой розы (рис. 1). Исследуются геометрические образы границ оболочки, которые являются окружностью. В рассматриваемой декартовой системе координат центр окружности совпадает с центром координат. Радиус окружности равен радиусу оболочки. Уравнение, описывающее окружность, имеет следующий вид ![]() . Геометрический образ сердечника составлен из трех эллипсов с общим центром, с одинаковыми малыми и большими радиусами и развернутых относительно друг друга на
. Геометрический образ сердечника составлен из трех эллипсов с общим центром, с одинаковыми малыми и большими радиусами и развернутых относительно друг друга на ![]() .
.
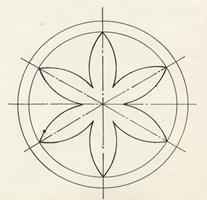
Рисунок 1. Волоконный световод с подвешенной профильной жилой
Уравнение эллипса:
![]() ;
;
где: a — радиус эллипса по оси OX,
b — радиус эллипса по оси OY.
Уравнения преобразования координат (поворот осей координат на угол φ):
![]() ;
; ![]() .
.
В данном случае j=60°, откуда получаются соотношения x=(3y)1/2 и y=-(3x)1/2. Подставляя по очереди полученные соотношения в уравнение эллипса, можно записать:
|
|
|
|
|
|
|
|
Таким образом, получаются точки пересечения двух эллипсов:
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, что точки 3 и 4 лежат внутри третьего эллипса, который развернут относительно первого на угол 120° или –60°. Таким образом, важна только точка 1. Точка 2 получается из точки 1 при повороте точки 1 относительно центра на угол 180°. Все интересующие точки можно найти, поворачивая точку 1 на углы, кратные 60° (60°, 120°, 180°, 240°, 300°). Координаты точки 1:
|
|
|
Уравнение преобразования координат — поворот на угол φ и смещение по осям:
|
|
|
Подставляя в уравнения преобразования координаты точки 1, можно получить координаты точек пересечения эллипсов. Геометрическим образом границы сердцевины будут дуги эллипсов, ограниченных точками пересечения.
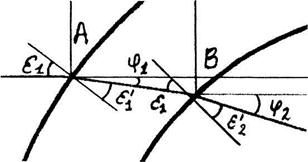
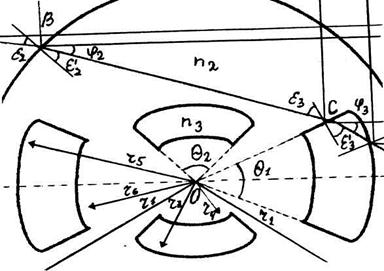
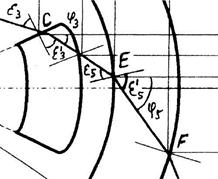
Геометрическим образом траектории движения луча являются отрезки прямых, концами которых являются точки пересечения прямых и границ оболочек и сердцевины (рис. 2).
Из рис. 2 и 3 вытекают формулы:
|
|
|
|
|
|
|
|
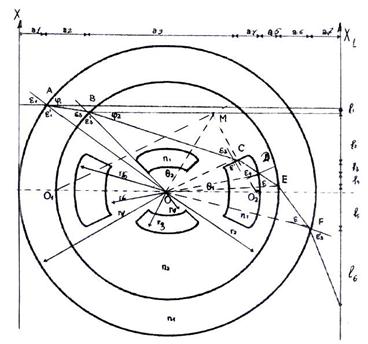
Рисунок 2. Траектория движения основного зондирующего луча
|
|
|
Рисунок 3. Вход луча в волоконную структуруРисунок 3. Вход луча в волоконную структуру |
Рассмотрим ▲ВОС и параллельные прямые ВМ и ОО1 с секущей ВО (рис. 2, 3):
|
|
|
|
|
|
|
|
По закону Снелля:
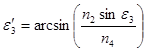 .
.
Из геометрических соображений:
![]() .
.
|
|
|
Рисунок 4. Рефракция зондирующего луча |
Из ▲BOC по теореме синусов (рис. 2, 4):
|
|
|
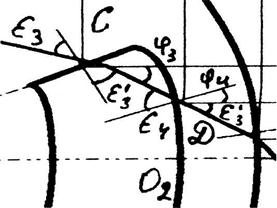
Из ▲COD по теореме синусов (рис.2, 5):
|
|
|
Из геометрических соображений:
![]() .
.
|
|
|
Рисунок 5. Зондирование сердцевины волоконной структуры |
Из ▲DOE по теореме синусов (рис. 2, 6):
|
|
|
Из закона Снелля:
![]()
Из геометрических соображений:
![]() .
.
|
|
|
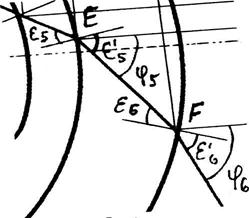
Рисунок 6. Распространение зондирующего луча на выходе из структуры |
Из ▲EOF по теореме синусов (рис.2, 6):
|
|
|
По закону Снелля:
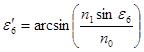 .
.
Из геометрических соображений:
![]() .
.
|
|
|
Рисунок7. Формирование траектории выхода луча |
Из ▲AOB по теореме синусов (рис.2):
|
|
|
Из ▲BOC по теореме синусов:
|
|
|
Из ▲COD по теореме синусов:
|
|
|
Из ▲DOE по теореме синусов:
|
|
|
Из ▲EOF по теореме синусов (рис.2,7):
|
|
|
Проекции луча на горизонтальную ось имеют вид (рис.2):
|
|
|
|
|
|
|
|
|
|
||
Проекции луча на ось x1 записываются следующим образом:
|
|
|
|
|
|
|
|
Окончательно получаем координату отклонения луча:
![]()
Проекция луча на горизонтальную ось внутри световода:
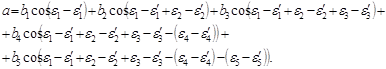
Интенсивность луча равна:
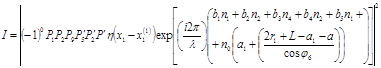 ,
,
где: ![]() ,
,
![]() — коэффициент поглощения материала.
— коэффициент поглощения материала.
Математическое обеспечение программы для расчета прохождения луча в многослойных фигурах, состоящих из окружностей, дуг и радиальных прямых. Для решения задачи используется декартова система координат, точка — А с координатами — X0 и Y0, вектор — а с углом наклона к оси — X и модулем — m.
Так как внешняя фигура является окружностью, то вторая точка вычисляется по формуле ![]() ,
, ![]() . Все последующие точки вычисляются по формулам:
. Все последующие точки вычисляются по формулам:
1. вектор и окружность —
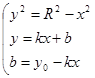
α — угол наклона вектора, ![]() —
— ![]() .
.
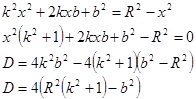
*![]()
![]()
модуль выбора
![]() .
.
2. вектор и прямая —
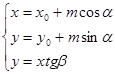
α — угол наклона вектора, β — угол нормали.
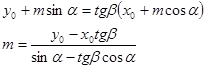 .
.
3. для расчета угла падения —
|
|
|
а — вектор луча, b — вектор нормали.
4. для расчета угла преломления —
![]()
γ — угол падения,
γ2 — угол преломления,
n1, n2 — коэффициенты.
5. для перерасчета угла наклона вектора к оси X используются четыре дополнительных вектора. Два вектора направлены перпендикулярно к линии фигуры и два вектора направлены по касательной к линии фигуры — ![]() — векторы нормали (углы),
— векторы нормали (углы), ![]() — векторы касательной (углы).
— векторы касательной (углы).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α — угол наклона вектора,
β — угол нормали.
Основные типы характеристических лучей, вносящих максимальный вклад в картину рассеяния, сведены в табл. 1.
Таблица 1.
Формулы вычисления основных типов характеристических лучей
|
|
где
|
|
|
где
|
|
|
где
|
|
|
где
|
|
|
где
|
|
|
где
|
|
|
где
|
|
|
где
|
|
|
где
|
Рассмотренный выше метод зондирования волоконных структур различных типов позволяет вычислить геометрические и оптические параметры световодов широкого диапазона применения.
Список литературы:
1.Андросик А.Б., Мировицкая С.Д. Моделирование градиентных оптических волокон рефракционным методом. В кн.: Информационные технологии: Приоритетные направления развития. Книга 8. — Новосибирск: ООО «Сибпринт». — 2012. — 227 с.
2.Лазарев Л.П., Мировицкая С.Д. Контроль геометрических и оптических параметров волокон. — М.: Радио и связь, 1988. — 280 с.
дипломов


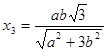
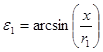
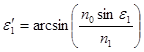
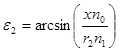
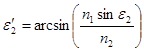
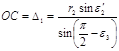 .
.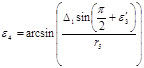 .
.
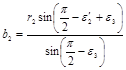 .
.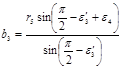 .
.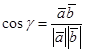 ,
,
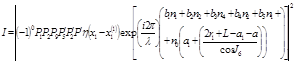
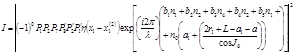
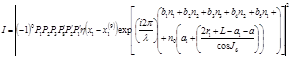
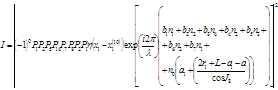
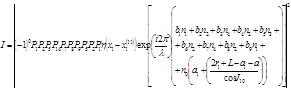
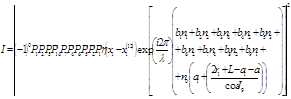
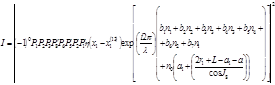
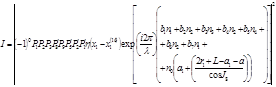
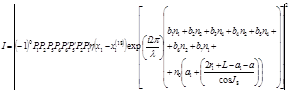
Оставить комментарий