ИНТЕГРИРОВАНИЕ  УРАВНЕНИЙ  ДВИЖЕНИЯ  МАТЕРИАЛЬНОЙ  ТОЧКИ  В  ЦЕНТРАЛЬНЫХ  ПОЛЯХ  И  УРАВНЕНИЯ  В  ВАРИАЦИЯХ

Бабаджанянц  Левон  Константинович

д-р  физ.-мат.  наук,  профессор  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт-Петербург

E -mail:  levon@mail.wplus.net

Брэгман  Анна  Михайловна

студент  Санкт-Петербургского  государственного  университета,

РФ,  г.  Санкт-Петербург

E -mail:  meune@mail.ru

Брэгман  Константин  Михайлович

старший  преподаватель  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт-Петербург

E -mail:  beswdw@gmail.com

Петросян  Леон  Аганесович

д-р  физ.-мат.  наук,  профессор  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт- Петербург

E-mail: 

INTEGRATION  OF  EQUATIONS  OF  MOTION  OF  A  MATIRIAL  POINT  IN  CENTRAL  FIELDS  AND  EQUATIONS  OF  VARIATIONS

Levon  Babadzanjanz

doctor  of  Science,  professor  of  Saint-Petersburg  State  University,  Russia,  Saint-Peretsburg

Anna  Bregman

student  of  Saint-Petersburg  State  University,  Russia,  Saint-Peretsburg

Konstantin  Bregman

senior  Lecturer  f  Saint-Petersburg  State  University,  Russia,  Saint-Peretsburg

Leon  Petrosyan

doctor  of  Science,  professor  of  Saint-Petersburg  State  University,  Russia,  Saint-Peretsburg

Работа  выполнена  при  поддержке  гранта  СПбГУ  9.37.345.2015.

АННОТАЦИЯ

Для  применения  предложенного  нами  ранее  алгоритма  решения  уравнений  в  вариациях  для  задачи  о  движении  материальной  точки  в  центральном  силовом  поле  с  возмущением  необходимо  знать  общее  решение  невозмущенных  уравнений  (то  есть  уравнений  движения  точки  в  соответствующем  центральном  поле).  Как  известно,  решение  любых  таких  уравнений  можно  получить  в  квадратурах,  однако  отнюдь  не  всегда  эти  квадратуры  можно  выразить  в  терминах  известных  специальных  функций.  Более  того,  упомянутый  выше  алгоритм  основан  на  уравнении  для  специальной  переменной  s,  которое  зависит  от  невозмущенного  решения  и  потенциала.  В  настоящей  работе  мы  рассматриваем  ряд  применяемых  на  практике  центральных  потенциалов,  для  которых  решение  невозмущенных  уравнений  выражается  в  терминах  известных  специальных  функций.  Для  всех  этих  случаев  мы  получаем  уравнение  для  вспомогательной  функции  s,  что  гарантирует  практическую  применимость  упомянутого  выше  алгоритма. 

ABSTRACT

To  apply  the  algorithm  of  solving  the  equations  of  variations  to  the  problem  of  motion  of  a  material  point  in  perturbed  central  force  field,  which  authors  have  proposed  earlier,  one  has  to  know  the  general  solution  of  the  unperturbed  equations  (that  is,  the  equations  of  motion  of  a  material  point  in  corresponding  central  field).  As  is  known,  such  equations  are  solvable  by  quadratures,  but  it  does  not  always  happen  that  the  corresponding  solutions  one  can  represent  in  terms  of  known  special  functions.  What  is  more,  the  above-mentioned  algorithm  is  based  on  the  equation  to  the  special  variable  s,  which  depends  on  the  unperturbed  solution  and  the  potential.  In  this  study,  we  consider  a  number  of  real-world  potentials  that  allow  representing  solutions  in  terms  of  known  special  functions  and,  in  all  these  cases,  to  guarantee  the  practical  applicability  of  the  algorithm  mentioned  we  derive  the  corresponding  equation  to  s.

Ключевые  слова :  центральное  силовое  поле;  уравнения  движения;  уравнения  в  вариациях.

Keywords:  central  force  field;  equations  of  motion;  equations  of  variations.

1.  Введение

В  статьях  [4;  5]  был  предложен  метод  решения  уравнений  в  вариациях  в  декартовых  координатах  для  случая  движения  материальной  точки  в  произвольном  возмущенном  центральном  поле.  Для  применения  его  к  конкретным  практическим  задачам  предварительно  необходимо  [4;  5]:

·получить  общее  решение  невозмущенных  уравнений,

·выписать  уравнение  для  вспомогательной  переменной  s.

Хотя  решение  уравнений  движения  материальной  точки  в  центральном  силовом  поле  всегда  можно  найти  в  квадратурах,  представить  его  через  известные  функции  получается  отнюдь  не  всегда,  а  тогда  и  уравнение  для  s  не  выписать.  Как  известно,  уравнение  движения  в  центральном  поле  определяются  тем  или  иным  центральным  потенциалом.  В  настоящей  работе  мы  рассмотрим  ряд  важных  практически  значимых  уравнений  движения  точки  в  центральных  полях,  определяемых  различными  центральными  потенциалами,  и  выпишем  для  них  соответствующие  уравнения  для  s,  что  обеспечит  перспективу  построения  в  дальнейшем  приближенных  моделей  движения  точки  в  соответствующих  возмущенных  центральных  силовых  полях.  В  настоящем  разделе  приводится  следующий  необходимый  далее  материал:

·уравнение  движения  точки  в  центральном  поле,

·два  способа  решения  уравнений  движения  в  квадратурах,

·уравнение  для  s,

·список  рассматриваемых  в  работе  центральных  потенциалов.

В  следующем  разделе  мы  приведем  решения  уравнений  движения  для  этих  потенциалов  и  соответствующие  уравнения  для  функции  s.

1.1 Уравнение  движения  точки  в  центральном  поле

Рассмотрим  в  системе  координат    уравнение  Ньютона  движения  материальной  точки  массы    под  действием  силы  ,  :  .  Функция    называется  стационарным  силовым  полем  (то  есть  точка    движется  в  силовом  поле  ).  Если  существует  функция    такая,  что  ,  то  ее  называют  потенциалом  поля  ,  а  само  это  поле  называют  потенциальным.  Поле  центральное,  если  существует  точка    (центр  сил)  такая,  что  на  любую  материальную  точку  действует  сила,  направленная  по  прямой,  проходящей  через  эту  точку  и  центр  сил  и  зависящая  только  от  расстояния  от  этой  точки  до  центра  сил.  Центральное  поле  имеет  потенциал  ,  а  уравнение  Ньютона  движения  материальной  точки  в  таком  поле  имеет  вид  [3]:

  (1)

1.2  Два  способа  решения  уравнения  движения  точки  в  центральном  поле 

Как  известно  [3],  уравнение  (1)  имеет  три  скалярных  интеграла  площадей  ,  которые  можно  записать  в  виде  одного  векторного  равенства

  (2)

(  —  интеграл  площадей,  а    и    —  постоянные  площадей).  Из  интегралов  площадей  следует,  что  точка  в  центральном  поле  движется  в  плоскости  Лапласа  ,  проходящей  через  центр  сил  .  Систему    свяжем  условием  ,    (то  есть  ),  тогда  плоскость  Лапласа  ортогональна    и  задается  равенством  .  Если  рассмотреть  движение  точки    в  плоскости  Лапласа  в  цилиндрических  координатах    при  ,  то  из  (2)  можно  получить  равенство

,  (3)

которое  также  называют  интегралом  площадей.

Так  как  проекция    на  направление    равна  ,  то  проектируя  (1)  на  ,  получаем  ,  а  учитывая  еще  (3)  приходим  к  уравнению:

  (4)

При    можно  получить  из  (4)  уравнение  Бине  для    как  функции  от  :  так  как

,  ,

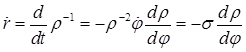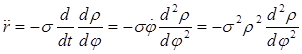то  уравнение  Бине  имеет  вид:

.  (5)

Получим  решение  уравнений  (4),(5)  в  квадратурах.  При  начальных  условиях

  получаем:

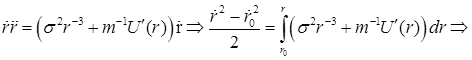
  (6)

.

При    аналогично  решаем  уравнение  (5):  также  при  начальных  условиях

  получаем:  так  как 

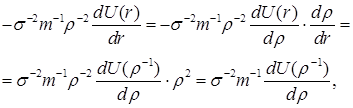
то:

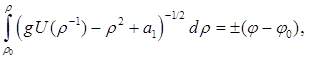  (7)

Формулу  (7)  естественно  использовать  для  определения  траектории  в  виде  ,  а  формулу  (6)  —  для  нахождения  решения 

1.3 Центральные  потенциалы

Здесь  мы  приводим  ряд  центральных  потенциалов,  для  которых  удается  представить  квадратуры  (6)  и/или  (7)  в  терминах  элементарных  или  других  специальных  функций  математической  физики.  Сами  эти  представления  мы  получим  в  разделе  2.  При  выборе  практически  важных  реальных  моделей  потенциалов  мы  пользовались  литературой  [1;  2;  6;  8;  9]. 

1.3.1        Точечные  потенциалы

Так  называют  потенциалы,  создаваемые  одной  точечной  массой  или  одним  точечным  зарядом.

Произвольный  степенной  потенциал

Потенциал  Ньютона 

  (  потенциал  Кулона)

Потенциал  Гука  (притяжения  (-)  и  отталкивания  (+))

Потенциал  притяжения  Ван-дер-Ваальса-Кизома

Потенциал  притяжения  Ван-дер-Ваальса-Дебая,  Лондона

1.3.2 Объемные  потенциалы

При  сферически-симметричном  распределении  масс  или  зарядов  возникает  центральное  поле  в  области  пространства,  занимаемой  шаром  конечного  или  бесконечного  радиуса.  Оно  называется  центральным  полем  объемных  масс  или  зарядов.  Различают  в  этом  случае  два  поля  —  внешнее  (вне  шара)  и  внутреннее  (внутри  шара).  Соответствующие  потенциалы  называют  внешним  и  внутренним.  По  теореме  Ньютона  внешний  потенциал  равен  потенциалу  материальной  точки,  сосредоточенной  в  центре  шара  и  имеющей  массу,  равную  суммарной  массе,  распределенной  в  шаре.  Если  радиус  упомянутого  выше  шара  конечен,  будем  обозначать  его  .

Потенциал  однородного  шара

Если  плотность  массы  в  шаре  задается  формулой

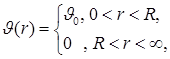
то 

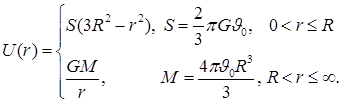
Потенциал  шара  с  линейным  убыванием  плотности

Если  плотность  массы  в  шаре  задается  формулой

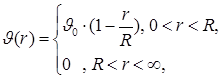
то

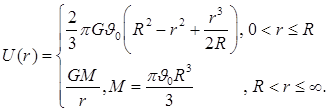
Модель  Шустера  потенциала  звездного  скопления

Если  плотность  массы  в  шаре  задается  формулой

то

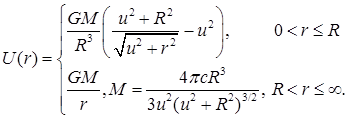
2.  Представление  движения  точки  в  центральном  поле  для  различных  потенциалов  и  соответствующие  уравнения  для  переменной  s

Прежде  всего,  напомним  здесь  уравнение  для  ,  которое  лежит  в  основе  метода  решения  уравнений  в  вариациях,  предложенного  в  работе  [1]:

    (8)

где  зависит  от  невозмущенного  решения,  потенциала  и  возмущений  (см.  [1]).  В  следующих  разделах,  кроме  выражений  квадратур  для  рассматриваемых  потенциалов,  мы  приводим  и  соответствующие  функции  . 

2.1  Выражение  квадратур  и  уравнения  для    для  точечных  потенциалов

Произвольный  степенной  потенциал

  ; 

Квадратура  (6)  принимает  следующий  вид: 

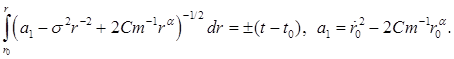
Интеграл  слева  выражается  через  гипергеометрическую  функцию  Гаусса    при  любом  действительном  ,  например,  при  помощи  Wolfram  Mathematica  [10].  Если  ,  а    рациональное  число,  то  подынтегральное  выражение  слева  является  биномиальным  дифференциалом:  при  таких    этот  интеграл  можно  выразить  в  терминах  элементарных  функций  в  трех  случаях:    (законы  Ньютона  и  Кулона),  (закон  Гука),  а  также  при  . 

Потенциал  Ньютона

  ;  .

Используем  уравнение  (5)  при  ,  :

.  (9)

Его  решение  дается  формулой

,

где    —  произвольные  постоянные.  Поэтому:

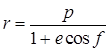,.  (10)

Это  уравнение  конического  сечения  с  началом  в  центре  сил    и,  одновременно,  фокусе  конического  сечения.  Величины    и    —  это  соответственно  параметр  и  эксцентриситет  конического  сечения,  а    —  истин-ная  аномалия.  Уравнение  (10)  описывает  три  вида  конических  кривых:  эллипс  (),  параболу  ()  и  гиперболу  ().

Потенциал  Гука

  .

Используем  равенство  (7)  при  ,  .  При    получаем: 

  ,

,  ,  .

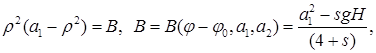
Теперь  используем  (6)  теперь  также  при  ,  но  при  любом  :

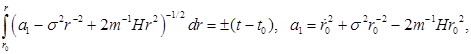
Замена    дает    и,  так  как    то  (см.  [7],  1.2.52  -  8)  получаем:

.

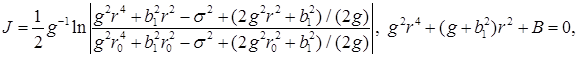
Потенциал  Ван-дер-Ваальса  –  Кизома

,  .

Используем  (7)  при  ,  .  При  ,  получаем:

Интеграл  слева  выражается  через  неполный  эллиптический  интеграл    (например,  при  помощи  Wolfram  Mathematica).

Потенциал  Ван-дер-Ваальса  –  Дебая,  Лондона

,  .

Используем  (7)  при  ,  .  При  ,  получаем:

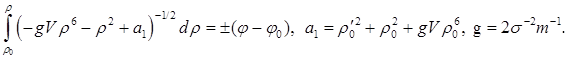
Интеграл  слева  можно  выразить  через  неполный  эллиптический  интеграл    (например,  при  помощи  Wolfram  Mathematica).

2.2  Выражение  квадратур  и  уравнения  для    для  объемных  потенциалов

Потенциал  однородного  шара

,    

Используем  равенство  (6)  при  любом  :

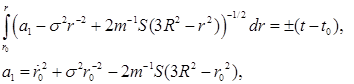
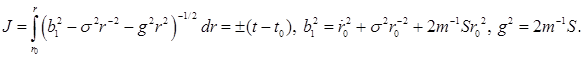
Замена    дает

и,  так  как  то  при    (см.  [7],  1.2.52-10)  получаем: 

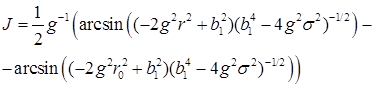
то  есть:

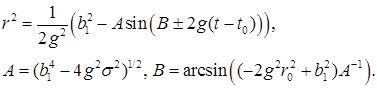
Используя  теперь  (7)  при  ,    и  ,  получаем:

  ,

,

.

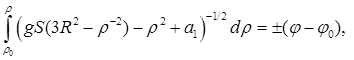
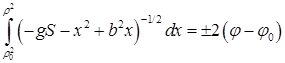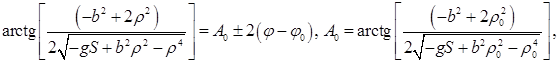
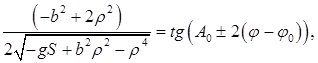
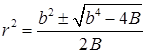Потенциал  шара  с  линейным  убыванием  плотности

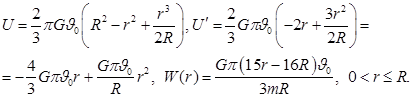
Используем  равенство  (6):

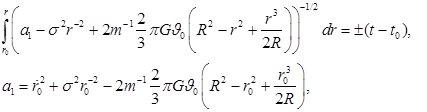
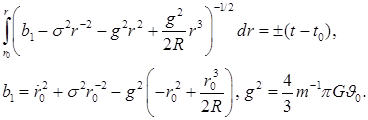
При  интеграл  слева  выражается  через  неполный  эллиптический  интеграл  ,  но  при    он  через  известные  функции  не  выражается.  Аналогичный  результат  получаем  при  использовании  равенства  (7).

Модель  Шустера  потенциала  звездного  скопления

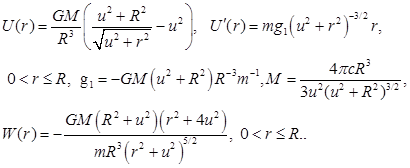
Используем  равенство  (6):

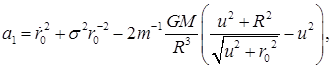
Замена    дает:

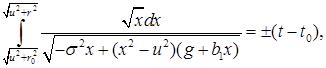
Этот  интеграл  выражается  через  неполный  эллиптический  интеграл    (например,  при  помощи  Wolfram  Mathematica).

3.  Заключение

Таким  образом,  в  настоящей  статье  мы  проделали  важную  подготовительную  работу  с  тем,  чтобы  иметь  возможность  в  дальнейшем  применять  алгоритм  решения  уравнений  в  вариациях,  предложенный  нами  в  статьях  [1;  2]:  в  разделе  2  квадратуры,  представляющие  решение  уравнений  движения  материальной  точки  в  центральном  поле,  представлены  в  терминах  элементарных  и  специальных  функций  для  различных  реальных  моделей  центральных  полей,  а  также  для  всех  рассмотренных  полей  выписаны  уравнения  для  функции    (это  уравнение  лежит  в  основе  упомянутого  выше  алгоритма).  Нам  удалось  осуществить  все  сказанное  для  центральных  полей,  определяемых  следующими  потенциалами:  произвольным  точечным  степенным  потенциалом  (в  частности,  потенциалами  Ньютона,  Кулона,  Гука,  Ван-дер-Ваальса-Кизома,  Ван-дер-Ваальса-Дебая-Лондона),  а  также  объемными  потенциалами  —  однородного  шара,  шара  с  линейным  убыванием  плотности  и  Шустера  для  звездных  скоплений.

Список  литературы:

1. Антонов  В.  Элементы  теории  гравитационного  потенциала  и  некоторые  случаи  его  явного  выражения.  /  В.  Антонов,  И.  Никифоров,  К.  Холшевников  //  СПб.:  Изд.  СПбГУ,  2008.  —  208  с.
2. Антонов  В.  Введение  в  теорию  ньютоновского  потенциала.  /  В.  Антонов,  Е.  Тимошкова,  К.  Холшевников  //  М.:  Наука,  1988.  —  270  с. 
3. Бабаджанянц  Л.  Классическая  механика  /  Л.  Бабаджанянц,  Ю.  Пупышев,  Ю.  Пупышева  //  СПб.  СОЛО.  2007.  —  240  с.
4. Бабаджанянц  Л.  Об  уравнениях  в  вариациях  в  задаче  о  движении  точки  в  возмущенном  центральном  поле  /  Л.  Бабаджанянц,  А.  Брэгман,  К.  Брэгман,  П.  Касикова  //  НП  «СибАК»,  Сборник  статей  XXXI  Межд.  Конф.,  Секция  7:  Аэрокосмическая  техника  и  технологии.  —  №  2(27).  —  2014.  —  C.  83—91.
5. Бабаджанянц  Л.  К  задаче  о  движении  точки  в  возмущённом  центральном  поле:  о  построении  рядов  по  малому  параметру  /  Л.  Бабаджанянц,  А.  Брэгман,  К.  Брэгман,  П.  Касикова  //  Астрономический  циркуляр.  Государственный  астроном.  институт  им.  П.К.  Штернберга  МГУ,  —  №  1608.  —  2014.  —  С.  1—3.
6. Кондратьев  Б.  Теория  потенциала  (Новые  методы  и  задачи  с  решениями)  /  Б.  Кондратьев  //  М.:  Мир,  2007.  —  512  с.
7. Прудников  А.  Интегралы  и  ряды  /  А.  Прудников,  Ю.  Брычков,  О.  Маричев  //  М.:  Наука.  1981.  —  800  с. 
8. Сретенский  Л.  Теория  ньютоновского  потенциала  /  Л.  Сретенский  //  М.:  ОГИЗ,  ГИТТЛ,  1946.  —  322  с.
9. Учайкин  В.  Механика.  Основы  механики  сплошных  сред.  Задачи  и  упражнения  /  В.  Учайкин  //  М.:  ИКИ,  2002.  —  179  с.
10. Wolfram  Mathematica  Documentation  Center  //  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://reference.wolfram.com/mathematica/guide/Mathematica.html