Статья опубликована в рамках: XLVIII-XLIX Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 26 августа 2015 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
УЛУЧШЕНИЕ ОДНОГО ИЗ ПРОТОКОЛОВ СОГЛАСОВАНИЯ КЛЮЧЕЙ
Кротова Елена Львовна
канд. физ.-мат. наук, доцент Пермского национального исследовательского политехнического университета
РФ, г. Пермь
E-mail:
Андреев Роман Александрович
студент Пермского национального исследовательского политехнического университета
РФ, г. Пермь
Е-mail:
Бадртдинов Артём Сергеевич
студент Пермского национального исследовательского политехнического университета
РФ, г. Пермь
Е-mail:
Феофилова Полина Андреевна
студент Пермского национального исследовательского политехнического университета
РФ, г. Пермь
Е-mail : feofilovap@gmail.com
ONE OF THE KEY AGREEMENT PROTOCOLS IMPROVING
Elena Krotova
candidate of physical and mathematical sciences, docent of Perm National Research Polytechnic University
Russia, Perm
Roman Andreev
Student of Perm National Research Polytechnic University
Russia, Perm
Artem Badrtdinov
Student of Perm National Research Polytechnic University
Russia, Perm
Polina Feofilova
Student of Perm National Research Polytechnic University
Russia, Perm
АННОТАЦИЯ
Представлено повышение безопасности протокола согласования ключей, основанного на использовании матриц Адамара, который предложили Чан-Хуэй Хо и Мун Хо Ли. Показано слабое место предложенного протокола, и была увеличена его безопасность.
ABSTRACT
In this paper, the security of key agreement protocol based on Sylvester Hadamard matrices proposed by Chang-hui Choe and Moon Ho Lee has been improved. The weakness of their protocol was introduced and its security was increased.
Ключевые слова: шифрование; безопасность; согласование ключей.
Keywords: encryption; security; key agreement.
Протоколы согласования ключей позволяют двум или более сторонам обмениваться информацией между собой через незащищенную сеть и согласовывать общий ключ сеанса, который может быть использован для последующего безопасного общения между сторонами. Таким образом, безопасные протоколы согласования ключей выступают в качестве составного блока для сложных протоколов более высокого уровня [1; 6; 2]. Метод согласования ключей с использованием матриц Адамара был предложен в [3]. Повышение безопасности этого протокола, сделает его очень подходящим для согласования ключей в ограниченных условиях.
Матрица Адамара H порядка ![]() является
является ![]() матрицей с элементами
матрицей с элементами ![]() , столбцы которой ортогональны, так что справедливо соотношение
, столбцы которой ортогональны, так что справедливо соотношение ![]() , где
, где ![]() ― единичная матрица размера
― единичная матрица размера ![]() . Учитывая, что матрица
. Учитывая, что матрица ![]() порядка
порядка ![]() , то матрица порядка
, то матрица порядка ![]() будет выглядеть следующим образом:
будет выглядеть следующим образом:
![]() (1)
(1)
Матрицы вида (1) называются матрицами Сильвестра Адамара и определены для всех степеней 2.
Начиная с ![]() , матрицы Адамара порядка
, матрицы Адамара порядка ![]() (обозначаются
(обозначаются ![]() ) могут быть образованы применением произведения Кронекера (
) могут быть образованы применением произведения Кронекера (![]() ) к
) к ![]() экземплярам
экземплярам ![]() . Ниже представлена матрица Адамара степени 2:
. Ниже представлена матрица Адамара степени 2:
![]() (2)
(2)
![]() также может быть записан следующим образом:
также может быть записан следующим образом:
![]() (3)
(3)
где: ![]() — номер строки,
— номер строки,
![]() — номер столбца
— номер столбца ![]() (начиная с 0),
(начиная с 0),
![]() — элемент
— элемент ![]() , расположенный в строке
, расположенный в строке ![]() и столбце
и столбце ![]() ,
,
![]() — скалярное произведение
— скалярное произведение ![]() и
и ![]() .
.
Если ![]() является конечной группой и
является конечной группой и ![]() является конечной абелевой группой, то коцикл является отображением
является конечной абелевой группой, то коцикл является отображением ![]() , удовлетворяющим уравнению коцикла:
, удовлетворяющим уравнению коцикла:
![]() (4)
(4)
Групповая операция ![]() с матрицами Адамара определяется как побитовое исключающее ИЛИ.
с матрицами Адамара определяется как побитовое исключающее ИЛИ.
Коцикл естественно отображается в виде коциклических матрицы, которая является квадратной матрицей, строки и столбцы индексированными элементами ![]() при некотором фиксированном порядке, и вступление которых в положении
при некотором фиксированном порядке, и вступление которых в положении ![]() является
является ![]() (в другом месте это называется чистой коциклической матрицей) пишем:
(в другом месте это называется чистой коциклической матрицей) пишем:
![]() (5)
(5)
Теорема 1: матрицы Адамара являются коциклическими [4].
Секретный ключ, созданный двумя пользователями и одним доверенным центром (Trusted Authority — TA) с помощью тех же матриц Адамара. Процесс согласования ключей, предложенный в [3]:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
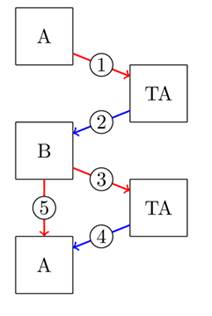
Рисунок 1. Процесс согласования ключей
К сожалению, предложенный протокол не является безопасным из-за следующих причин:
· ![]() и
и ![]() не шифруются и враг может просто найти
не шифруются и враг может просто найти ![]() с помощью перебора. Он может получить
с помощью перебора. Он может получить ![]() и найти ключ сессии
и найти ключ сессии ![]() путем перехвата сообщений между
путем перехвата сообщений между ![]() и
и ![]() .
.
· В этом протоколе (шаг 2), B может вычислить ![]() следующим образом:
следующим образом:
1. ![]() расшифровывает
расшифровывает ![]() и находит
и находит ![]() .
.
2. Так как ![]() имеет
имеет ![]() он может найти
он может найти ![]() , рассчитав
, рассчитав ![]() .
.
Таким образом, ключ сеанса ![]() уязвим.
уязвим.
Увеличение безопасности происходит следующим образом. Доверенный центр раздает секретный ключ ![]() ,
, ![]() и
и ![]() разрядное число
разрядное число ![]() . После согласования ключа, A и B делятся секретным общим ключ
. После согласования ключа, A и B делятся секретным общим ключ ![]() . Пользователи могут поделиться
. Пользователи могут поделиться ![]() -битным ключем сессии
-битным ключем сессии ![]() с помощью
с помощью ![]() матрицы Адамара и
матрицы Адамара и ![]() -битным числом
-битным числом ![]() и
и ![]() , которые могут быть разделены на
, которые могут быть разделены на ![]()
![]() -битных чисел, таких как
-битных чисел, таких как ![]() , где
, где ![]() . Новый процесс согласования ключей выглядит следующим образом:
. Новый процесс согласования ключей выглядит следующим образом:
· ![]() случайным образом генерирует
случайным образом генерирует ![]() , шифрует его с помощью
, шифрует его с помощью ![]() и посылает зашифрованный текст в
и посылает зашифрованный текст в ![]() (1):
(1):
![]() (6)
(6)
· ![]() шифрует
шифрует ![]() с
с ![]() и отправляет его
и отправляет его ![]() (2):
(2):
![]() (7)
(7)
· ![]() расшифровывает
расшифровывает ![]() и получает
и получает ![]() из
из ![]() .
. ![]() случайным образом генерирует
случайным образом генерирует ![]() и вычисляет секретный общий ключ следующим образом:
и вычисляет секретный общий ключ следующим образом:
![]() (8)
(8)
После создания ![]() ,
, ![]() шифрует
шифрует ![]() с
с ![]() и посылает зашифрованное сообщение
и посылает зашифрованное сообщение ![]() . Также
. Также ![]() шифрует
шифрует ![]() с
с ![]() и отправляет его
и отправляет его ![]() .
.
![]() получает
получает ![]() и шифрует его с
и шифрует его с ![]() и отправляет его
и отправляет его ![]() (3, 4):
(3, 4):
![]() (9)
(9)
· ![]() расшифровывает сообщение, полученное от
расшифровывает сообщение, полученное от ![]() и получает
и получает ![]() . Поэтому
. Поэтому ![]() может вычислить
может вычислить ![]() и тот же шаг 3. Для подтверждения ключа,
и тот же шаг 3. Для подтверждения ключа, ![]() расшифровывает
расшифровывает ![]() , зашифровывает
, зашифровывает ![]() с помощью
с помощью ![]() и отправляет его
и отправляет его ![]() . B расшифровывает
. B расшифровывает ![]() для подтверждения(5):
для подтверждения(5):
![]() (10)
(10)
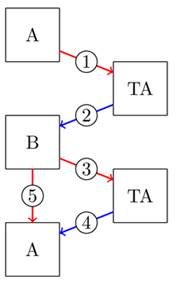
Рисунок 2. Улучшенный процесс согласования ключей
Авторы [3] показали, что вероятность каждого возможного ![]() -битного ключа сеанса в предлагаемом протоколе равна
-битного ключа сеанса в предлагаемом протоколе равна ![]() . Протокол согласования ключа, предложенный в [3] содержит недостатки, которые были показаны ранее. После шифрования
. Протокол согласования ключа, предложенный в [3] содержит недостатки, которые были показаны ранее. После шифрования ![]() и изменения протокола, была получена новая более безопасная версия протокола.
и изменения протокола, была получена новая более безопасная версия протокола.
Успешное управление ключами является важнейшим фактором для безопасности криптосистемы. На практике это, возможно, самый трудный аспект криптографии, потому что она включает в себя системную политику, обучение пользователей, организационные и ведомственные взаимодействия и координацию между всеми этими элементами. Протокол согласования ключа на основе криптографии с открытым ключом является дорогостоящим и он не подходит для сред с низкими мощностями вычисления. Вместо этого, был предложен симметричный протокол согласования ключей, являющийся достаточно безопасным и легким.
Список литературы:
- Ali Zaghian, Mohammad Jafar Hashemi, Ahmad Majlessi. Improving the Key Agreement Protocol Security Based on Hadamard Matrices / Journal of Mathematics and Computer Science 12 (2014), 316—319.
- Behrouz A. Forouzan, Cryptography and Network Security 2nd Edition, McGraw-Hill Education Pvt. Ltd., 2010
- Choe C.-h., M.H. Lee, Key agreement protocol using Sylvester Hadamard matrices, Journal of Communication and networks, Vol. 13, № 3,(2011) 1435—1443.
- Horadam K.J., P. Udaya, Cocyclic Hadamard codes, IEEE Trans.Inf. Theory, vol. 46, № 4, (2000) 545—1550.
- Horadam K.J., Hadamard Matrices, Princeton university Press 2007.
- Diffie W. and M. Hellman, New directions in cryptography, IEEE Trans.Inf. Theory, vol. 22,(1976) № 6, 644—654.
- Stallings W., Cryptography and Network Security principels and practice, 5 th ed., 2011.
дипломов


Оставить комментарий