СОПРОТВЛЕНИЕ  ФИБРОЦЕНТОВ  ДИНАМИЧЕСКИМ  НАГРУЗКАМ

Ахмеднабиев  Расул  Магомедович

канд.  тех.  наук,  доцент  Полтавского  национального  технического  университета  имени  Юрия  Кондратюка,  Украина,  г.  Полтава

E -mail:  arasul 49@mail.ru

Макаревич  Виктория

студент  Полтавского  национального  технического  университета  имени  Юрия  Кондратюка,  Украина,  г.  Полтава

Билик  Николай

студент  Полтавского  национального  технического  университета  имени  Юрия  Кондратюка,  Украина,  г.  Полтава

Карюк  Николай

студент  Полтавского  национального  технического  университета  имени  Юрия  Кондратюка,  Украина,  г.  Полтава

Шевчук  Андрей

студент  Полтавского  национального  технического  университета  имени  Юрия  Кондратюка,  Украина,  г.  Полтава

THE  RESISTENCE  OF  FIBER  REINFORCED  CEMENT  TO  DINAVIC  LOAD

Akhmednabi  R asul

associate  Professor  of  Poltava  National  Technical  Yuri  Kondratyuk  University,  Ukraine,  Poltava

Makarevich  Victoria

students  of  Poltava  National  Technical  Yuri  Kondratyuk  University,  Ukraine,  Poltava

Bilik  Nikolai

students  of  Poltava  National  Technical  Yuri  Kondratyuk  University,  Ukraine,  Poltava

Karyuk  Nikolai

students  of  Poltava  National  Technical  Yuri  Kondratyuk  University,  Ukraine,  Poltava

Andrey  Shevchuk

students  of  Poltava  National  Technical  Yuri  Kondratyuk  University,  Ukraine,  Poltava

АННОТАЦИЯ

Приведены  результаты  испытаний  на  динамические  нагрузки  цементного  камня,  армированного  полипропиленовым  волокном.  Рассчитаны  и  построены  в  полулогарифмических  координатах  линии  регрессии  по  средним  точкам,  линии  верхней  и  нижней  границ  доверительного  интервала  для  цементного  камня  и  композиций,  армированных  полипропиленовыми  волокнами. 

ABSTRACT

The  results  of  tests  on  the  dynamic  load  of  cement  stone,  reinforced  with  the  polypropylene  fibres.  Designed  and  built  in  the  n  semi-logarithmic  coordinates  the  regression  line  on  the  midpoint  line  of  the  upper  and  lower  limits  of  the  confidence  interval  for  the  cement  stone  and  compositions  reinforced  with  the  polypropylene  fibres.

Ключевые  слова:  цементный  камень;  полипропиленовое  волокно;  асимметрия  цикла;  частота  нагружения. 

Keywords:   cement  stone;  polypropylene  fiber;  asymmetry  cycle;  loading  frequency.

В  процессе  эксплуатации  на  конструкции  дорожных  сооружений  действуют  и  динамические  нагрузки.  Поэтому  стойкость  конструкций  против  динамических  нагрузок  имеет  важное  значение.

Процесс  разрушения  материалов  при  повторных  нагружениях  обычно  разбивают  на  три  этапа:  зарождение  микротрещины,  медленный  рост  ее  до  размера  трещины  Гриффитса,  и  наконец,  быстрое  распространение  трещины  до  катастрофического  разрушения  [3].  Полагают,  что  большая  часть  жизни  конструкции  приходится  на  второй  этап  медленного  роста  трещины.

Э.  Ву  [3]  при  повторных  нагружениях  композитов  предлагает  учитывать  три  основных  фактора:  I  —  процесс  вязкоупругого  разрушения;  2  —  историю  роста  трещины;  3  —  локальное  изменение  материала  вблизи  кончика  трещины.  На  основании  концепции  скачкообразного  распространения  трещины  он  сделал  вывод,  что  суммарное  приращение  трещины  увеличивает  сопротивление  росту  результирующей  трещины,  и  таким  образом  существует  сильное  влияние  геометрии  трещины  на  историю  ее  роста.  Очевидно,  важным  аспектом  разрушения  при  повторном  нагружении  композиционных  материалов  является  локальное  изменение  свойств  материала  в  окрестности  кончика  трещины.

В  данной  работе  на  повторные  нагрузки  испытывались  образцы-призмы  размерами  4x4x16  см,  изготовленные  из  глиноземистого  цемента  наполненные  полипропиленовыми  волокнами  диаметром  0,2  мм,  длиной  до  30  мм  и  объемным  содержанием  до  6  %.  Испытания  проводились  на  испытательной  машине  ГРМ-І.  Серии  образцов  состояли  из  15  штук,  по  три  из  которых  испытывались  для  определения  призменной  прочности. 

Исследования  [1;  2;  4],  проведенные  в  нашей  стране  и  за  рубежом,  показали,  что  динамическая  прочность  бетона,  армированного  различными  волокнами  значительно  выше  прочности  обычного  бетона.

Испытания  образцов  проводились  на  четырех  уровнях  нагружения,  которые  принимались  равными  0,9;  0,8;  0,7;  0,6  от  разрушающей  нагрузки,  коэффициент  асимметрии  цикла  напряжения    =  0,5.  Выбор  частоты  многократно  повторного  нагружения  осуществлялся  с  учетом  того,  что  в  конструкциях  величина  низких  частот  2—10  Гц  составляет  95  %,  и  она  принималась  равной  10  Гц.  На  каждом  уровне  испытывались  по  три  образца.  Для  сравнительной  оценки  наряду  с  исследуемыми  композициями  испытывались  образцы  чистого  цементного  камня  без  волокон.  Результаты  испытаний  приведены  в  табл.  1.

Таблица  1. 

Результаты  испытаний  чеканочных  композиций  на  выносливость

Примечание:  Композиция  2—14  —  объемное  содержание  волокна  2  %,  длина  волокна  14  мм

По  результатам  испытаний  построены  также  линии  регрессии,  устанавливаемые  уравнением  регрессии

    (1)

где:  А  і  В  —  коэффициенты,  определяются  по  результатам  испытаний;

  —  число  циклов,  соответствующие  разрушению  образца;

Коэффициенты  А  и  В  в  уравнении  (1)  вычисляются  по  результатам  испытаний,  по  выражению: 

    (2)

где:    ,  —  среднее  арифметические  значения  измеренных  величин;

    —  корреляционный  момент,  вычисляется  по  формуле:

    (3) 

где:    ,  —  дисперсии  переменных  величин,  вычисляемые  по  формулам:

    ;    (4)

n  —  число  образцов,  которые  разрушились.

Коэффициент  корреляции  вычисляется  по  формуле:

  (5)

его  величина  должна  находиться  в  диапазоне  -0,7˂  r  ˃  -1.0.

По  результатам  вычислений  получаем  уравнение  регрессии  для  чистого    цемента  по  средним  точками

    (6)

Доверительную  оценку  коэффициента  В  линии  регрессии  (1)  проводим  по  надежности  оценки  τ,  равной  0,95,  по  формуле

    ,  (7)

где  t  —  коэффициент  Стьюдента  при  числе  степеней  свободы 

  и  надежности  τ=  0,95.

Вычисляя  значение  доверительных  границ  по  формуле  (7),  получим  уравнение  линии  регрессии  верхней  границы  доверительного  интервала  для  цементного  камня  без  волокон  в  виде 

    (8)

и  уравнения  регрессии  нижней  границы  доверительного  интервала 

    (9)

по  которым  проводят  оценку  выносливости  материалов.

Подобным  образом  были  получены  уравнения  линии  регрессии  по  средним  точкам  и  гранам  доверительных  интервалов  для  композиций,  которые  приведены  ниже.

Композиция  2—14 

·     уравнение  линии  регрессии  по  средним  точкам

    (10)

·     уравнение  линии  регрессии  верхней  границы  доверительного  интервала

    (11)

·     уравнения  регрессии  нижней  границы  доверительного  интервала 

    (12)

Композиция  6—14:

·     уравнение  линии  регрессии  по  средним  точкам

    (13)

·     уравнение  линии  регрессии  верхней  границы  доверительного  интервала

    (14)

·     уравнения  регрессии  нижней  границы  доверительного  интервала 

    (15)

На  рис.  1—3  показаны  в  полулогарифмических  координатах  линии  регрессии  по  средним  точкам,  линии  верхней  и  нижней  границ  доверительного  интервала  для  цементного  камня  и  композиций.

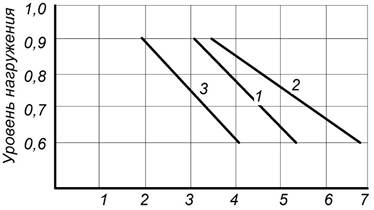
Рисунок  1.  Линии  регрессии  по  результатам  испытаний  на  выносливость  цементного  камня  без  волокон:  1  —  по  средним  точкам;  2  —  нижней  границы  доверительного  интервала;  3  —  верхней  границы  доверительного  интервала

Рисунок  2.  Линии  регрессии  по  результатам  испытаний  на  выносливость  состав  композиции  2—14:  1  —  по  средним  точкам;  2  —  нижней  границы  доверительного  интервала;  3-  верхней  границы  доверительного  интервала

Как  видно  из  приведенных  линий  регрессии,  с  увеличением  объемного  содержания  выносливость  композиции  увеличивается.  Так,  например,  композиции  с  содержанием  волокна  2  %  длиной  14  мм  имеют  выносливость  по  средним  значениям  на  базе  испытаний  3  *  циклов,  исчисленную  в  долях  от  призменной  прочности,  равную  0,683,  а  при  надежности  оценки  τ  =  0,95  на  той  же  базе  испытаний  она  составляет  0,517  (рис.  4).  С  увеличением  объемного  содержания  волокна  до  6  %  при  той  же  длине  те  же  показатели  составляют  соответственно  0,693  и  0,537  (рис.  4)

  Если  сравнивать  эти  показатели  для  чистого  цемента  (рис.  4)  и  испытываемых  композиций,  заметим,  что  для  чистого  цемента  они  составляют  соответственно  0,615  и  0,39,  что  меньше  на  10,1  и  24,4  %  чем  для  композиции  2—14. 

  Повышение  выносливости  волокнистых  композиционных  материалов  объясняется  тем,  что  волокна  вызывают  локальные  изменения  свойств  материала  в  окрестности  трещин,  в  результате  чего  трещина  распространяется  скачкообразно.  После  образования  трещины  доля  нагрузки,  передаваемая  на  волокна,  увеличивается.  При  кратковременной  нагрузке  в  волокнах  развиваются  упругие  деформации  и  волокна,  окруженные  со  всех  сторон  цементным  камнем,  как  бы  демпфируют.  Рост  трещин  при  этом  задерживается  вследствие  восприятия  волокнами  определенной  части  кратковременно  приложенной  нагрузки.  Кроме  того,  как  указывается  в  работе  [1],  с  ростом  длины  трещины  сопротивление  ее  распространению  в  волокнистых  композиционных  материалах  увеличивается.  Такой  механизм  вызывает  множественное  растрескивание  матрицы,  что,  однако,  не  приводит  к  разрушению  композита.  Очевидно,  при  повышенных  долях  максимальных  напряжений  от  призменной  прочности  процесс  растрескивания  матрицы  усиливается.  Матрица  растрескивается  на  мелкие  кусочки,  что  нарушает  совместную  работу  ее  с  волокнами  и  приводит  к  развитию  результирующей  трещины. 

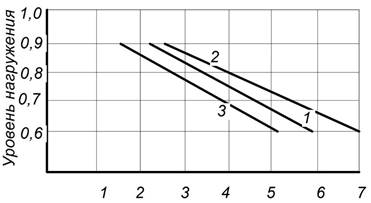
Рисунок  3.  Линии  регрессии  выносливости  для  состава  композиции  6—14:  1  —  по  средним  точкам;  2  —  верхней  границы  доверительного  интервала;  3  —  нижней  границы  доверительного  интервала

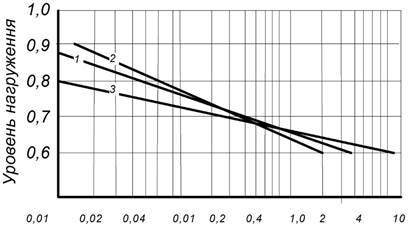
Рисунок  4.  Зависимость  между  уровнем  нагрузки  и  количеством  циклов  до  разрушения:  1  —  цемент  без  волокон;  2  —  композиция  2—14;  3  —  композиция  6—14.  Число  циклов  N =10⁶

С  уменьшением  отношения  максимальных  напряжений  к  призменной  прочности  процесс  растрескивания  матрицы  снижается,  уменьшается  нагрузка  на  волокна,  и  они  сохраняют  упругие  свойства  и,  как  следствие,  увеличивается  вклад  волокна  в  процесс  торможения  трещины.  Поэтому  с  повышением  объемного  содержания  волокна  повышается  выносливость  композиции,  что  демонстрируется  на  рисунке  4.

Этот  эффект  становится  очевидным  при  сравнении  зависимостей  между  уровнями  нагрузки  и  количеством  циклов  до  разрушения,  построенных  в  полулогарифмических  координатах  и  представленных  на  рисунке  4.

Из  приведенных  данных  видно,  что  в  исследуемых  композитах  при  высоких  уровнях  нагружения  происходит  быстрое  разрушение  матрицы  и  вклад  волокна  при  этом  незначительный.  Однако  с  понижением  уровня  нагрузки  выносливость  композиции  повышается.  В  образцах  цементного  камня  без  волокон  образовавшаяся  трещина  получает  дальнейшее  развитие  без  помех,  что  приводит  к  разрушению  образцов,  хотя  образования  трещины  происходит  на  поздней  стадии. 

Таким  образом,  испытания  показывают,  что  исследуемые  композиции  при  невысоких  значениях  уровня  загрузки  выносливее,  чем  образцы  цементного  камня.

Список  литературы:

1.Аболиньш  Д.С.,  Кравинскас  В.К.,  Лагутина  Г.Б.  Мелкозернистый  бетон,  армированный  обрезками  проволоки.  /Бетон  и  железобетон.  —  1975,  —  №  5,  —  с.  27.

2.Бродский  В.В.  Сопротивление  динамическим  импульсным  воздействиям  предварительно  напряженных  бетонных  элементов  и  железобетонных  колонн./  Диссертация  на  соискание  ученой  степени  кандидата  технических  наук.  2001  г.

3.Ву.  Э.  Прочность  и  разрушение  композитов.  В  кн.:  Композиционные  материалы,  т.  5.  М.,  Мир  1978.  —  c.  147.

4.Рузанов  П.А.  Математическое  моделирование  процессов  динамического  деформирования  и  разрушения  бетонов  в  двумерной  постановке.  Диссертация  на  соискание  ученой  степени  кандидата  технических  наук.  1999  г.