МЕТОДИКА  СТАТИЧЕСКОГО  РАСЧЕТА  НЕЛИНЕЙНЫХ  ПНЕВМАТИЧЕСКИХ  СООРУЖЕНИЙ  С  УЧЕТОМ  ГЕОМЕТРИЧЕСКОЙ  НЕЛИНЕЙНОСТИ

Амоян  Миша  Фрикович

студент  3  курса,  Саратовский  Государственный  Технический  Университет  имени  Гагарина  Ю.А.,  РФ,  г.  Саратов

E-mail:  ezid-007@yandex.ru

Алиев  Ариз  Алихан  оглы

студент  2  курса,  Саратовский  Государственный  Технический  Университет  имени  Гагарина  Ю.А.,  РФ,  г.  Саратов

E-mail:  164apple164@gmail.com

Ким  Алексей  Юрьевич

д-р  техн.  наук,  профессор  кафедры  ТСК,  Саратовский  Государственный  Технический  Университет  имени  Гагарина  Ю.А.,  РФ,  г.  Саратов

STATIC  CALCULATION  NONLINEAR  PNEUMATIC  STRUCTURES  TAKING  INTO  ACCOUNT  THE  GEOMETRIC  NONLINEARITY

Amoyan  Misha

3-d  year  student,  Saratov  State  Technical  University  named  after  Yuri  Gagarin,  Russia,  Saratov

Aliev  Ariz

2-nd  year  student,  Saratov  State  Technical  University  named  after  Yuri  Gagarin,  Russia,  Saratov

Kim  Alexey

doctor  of  Technical  Sciences,  professor  of  the  Department  “Theory  of  structures  and  constructions”,  Saratov  State  Technical  University  named  after  Yuri  Gagarin,  Russia,  Saratov

АНОТАЦИЯ

В  статье  излагается  методика  расчета  нелинейных  мембранно-пневматических  систем  с  учетом  геометрической  нелинейности.

Авторами  статьи  произведено  численное  исследование  статической  работы  пневматического  сооружения  итерационным  методом  последовательных  нагружений,  который  позволяет  учитывать  геометрическую  нелинейность  системы. 

ABSTRACT

The  article  describes  the  method  of  calculating  nonlinear  membrane-pneumatic  systems  taking  into  account  the  geometric  nonlinearity.

The  authors  have  produced  numerical  investigation  of  static  pneumatic  structures  iterative  method  of  successive  loadings,  which  allows  to  take  into  account  the  geometric  nonlinearity  of  the  system.

Ключевые  слова:  итерационный  метод;  мембранно-пневматические  сооружения;  вантово-стержневые  системы.

Keywords:   iterative  method;  membrane  pneumatic  constructions;  cable-core  system.

Пневматические  сооружения  появились  в  1949  году  с  помощью  серии  экспериментов,  в  отличие  от  других  сооружений  сразу  на  натурных  моделях.  Так  было  быстрее  и  дешевле.  Когда  были  нужны  десятки  таких  объектов,  этот  метод  оправдывал  себя,  лишь,  когда  в  шестидесятых  годах  прошлого  века  потребовалось  тысячи  таких  сооружений  спортивного  назначения  появились  методы  расчета. 

Задача  определения  напряженно-деформированного  состояния  воздухоопорных  оболочек  по  заданной  начальной  форме  и  известным  нагрузкам  в  то  время  решалась  на  основе  элементарной,  технической  и  математической  теорий  мягких  оболочек.

Для  расчета  воздухоопорных  оболочек,  объем  которых  нельзя  считать  замкнутым,  расчетчики  допускали  предположение  о  постоянстве  избыточного  давления.  При  сравнительно  медленном  нарастании  нагрузок  такая  предпосылка  вполне  приемлема.

При  быстро  же  растущих  нагрузках,  например  порывах  ветра,  правильнее  рассматривать  оболочку  как  замкнутый  объем,  так  как  воздух  при  быстро  меняющемся  объеме  в  таком  сооружении  не  успевает  полностью  выйти:  стравливающие  и  обратные  клапаны  мгновенно  не  срабатывают  и  оболочка  часто  рвалась.

К  началу  семидесятых  годов  прошлого  века  для  расчета  воздухоопорных  сооружений  стали  применять  следующие  программы:  LISA,  DIANA,  SOLVIA  в  них  использовали  метод  конечных  элементов  (МКЭ).  Конструкция  сооружения  расчленяется  на  множество  элементарных  конечных  элементов  (тросовый  элемент,  мембранный  элемент,  балочный  элемент  и  т.  д.),  реакции,  которых  на  приложенные  к  ним  деформации  и  усилия  программируются  для  автоматизированного  расчета  на  ЭВМ.  После  того  как  реальная  конструкция  представлена  расчетчиком  в  виде  совокупности  конечных  элементов,  ЭВМ  рассчитывает  по  программе  жесткостные  характеристики  всех  элементов  и  действующие  в  элементах  усилия,  объединяя  полученные  данные  в  систему  уравнений  равновесия.  В  результате  решения  разрешающей  системы  уравнений  определяются  перемещения  узлов,  по  которым  также  в  соответствии  с  программой  рассчитывают  деформации  и  напряжения  в  каждом  из  конечных  элементов.

Математическая  теория  мягких  оболочек  отличается  наиболее  строгим  подходом.  Ее  цель  —  определение  напряженно-деформированного  состояния  мягкой  оболочки  с  учетом  нелинейных  связей  как  между  деформациями  и  усилиями  (физическая  нелинейность),  так  и  между  деформациями  и  перемещениями  (геометрическая  нелинейность).  Теорию  отличает  сложность  уравнений,  которая  существенно  возрастает  при  дальнейших  уточнениях  расчетной  схемы,  например  при  учете  изменений  нагрузок  при  формоизменениях  оболочки  или  при  больших  её  деформациях.

Известные  методики  статического  расчёта  простейших  пневматических  систем  основаны  на  применении  как  линейной,  так  и  нелинейной  системы  интегро-дифференциальных  уравнений  равновесия  покрытия,  но  предполагают  постоянство  давления  воздуха  в  полости  при  нагружении,  т.  е.  Р  =  const.  или,  другими  словами,  предполагают,  что  в  уравнениях  V  =  const.,  где  V  —  объём  замкнутой  полости  покрытия.  В  то  же  время  расчётная  величина  давления,  постоянного  в  процессе  нагружения  системы,  в  необходимых  случаях  принималась  с  учётом  температуры  окружающей  среды  Т.  Программные  комплексы,  описанные  ранее,  не  создавались  для  расчёта  систем,  в  которых  герметичные  полости  существенно  изменяются  в  объёме  от  действия  нагрузок  [1].

При  расчете  мембранно-пневматических  систем  проф.  Ким  А.Ю.  предложил  учитывать  упругие  свойства  воздуха,  закаченного  в  герметически  замкнутую  полость  сооружения,  т.  е.  учитывать  влияние  на  давление  Р  упругих  перемещений  поясов  линзообразного  покрытия.  При  этом  приращение  объема  V  определяется  в  зависимости  от  давления  P  и  температуры  T  воздуха  в  замкнутой  полости  пневмолинзы.  Если  прежде  расчет  линзообразной  мембранно-пневматической  системы  сводился  проектировщиками  к  условному  расчету  предельного  состояния  её  несущего  и  напрягающего  поясов  в  отдельности.  Профессор  Ким  А.Ю.  создал  алгоритм,  который  позволил  учесть  сжимаемости  пневмолинзы  и  изменения  давления  воздуха  в  ней  от  совокупности  всех  параметров.  Прежний  приближенный  расчет,  далекий  от  описания  действительной  работы  сооружения,  не  всегда  позволял  проектировщикам  обеспечить  необходимую  надежность  и  долговечность  сооружения  (так,  около  половины  эксплуатируемых  мембранно-пневматических  сооружений  преждевременно  разрушилось  от  ветровых  нагрузок).  На  основании  данного  алгоритма  профессором  Кимом  А.Ю.  и  группой  аспирантов  была  создана  программа  «Пневматика»,  которая  позволяет  учитывать  упругие  свойства  воздуха,  закаченного  в  герметически  замкнутую  полость  сооружения,  Из  универсального  уравнения  состояния  газа

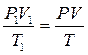  ,  (1)

объединяющего  известные  законы  Бойля-Мариотта  и  Гей-Люссака,  в  котором  параметры  P₁,  V₁,  T₁  характеризуют  систему  на  конечной  стадии  монтажа,  а  P⁰,  V⁰,  T⁰  на  начальной  стадии.  С  учетом  зависимостей  ,  ,    вывели    данную  формулу.  (2) 

Вычисляем  приращение  объема  DV  замкнутой  полости  (помещения,  пневмолинзы  или  нескольких  пневмолинз,  если  они  являются  сообщающимися  сосудами)  в  зависимости  от  вертикальных  прогибов  поясов  покрытия  на  произвольном  шаге  n  нагружения  системы.

  .  (3)

Данная  формула  позволяет  т.  е.  учитывать  влияние  на  давление  Р  упругих  перемещений  поясов  линзообразного  покрытия  при  изменении  геометрии  системы  сооружения.  Геометрическая  нелинейность  возникает  при  больших  перемещениях  и  деформациях  элементов,  что  сравнительно  часто  встречается  в  воздухоопорных  сооружениях.  Пакет  прикладных  программ  «Пневматика»  предназначен  для  статического  и  динамического  расчета  на  ЭВМ  плоских  и  пространственных  линзообразных,  воздухоопорных  и  комбинированных  мембранно-пневматических  систем  итерационным  методом  приращений  параметров  на  основе  континуальных  и  дискретных  расчётных  схем  с  учетом  геометрической  нелинейности  [2].

Численное  исследование  авторов  статьи  показало,  что  различие  между  экспериментальными  и  теоретическими  значениями  прогибов  линзообразного  покрытия  сооружения  и  его  модели  составило  5—14  %  для  локальных  нагрузок  и  5—8  %  для  распределенных  по  всему  пролету  нагрузок.  Давление  воздуха  в  пневмолинзе  при  этом  определяется  с  погрешностью  1—2  %  [2].

Исследования  авторов  статьи  показали,  что  отсутствие  учёта  нелинейной  упругости  воздуха,  заключённого  в  пневматические  полости,  при  расчёте  линзообразных  и  воздухоопорных  систем  может  исказить  вычисляемые  прогибы  или  усилия  в  поясах  в  два  раза  и  более.

Цель  исследований  состоит  в  создании  новых  конструктивных  форм  мембранно-пневматических  сооружений  гражданского  и  военного  назначения,  отличающихся  экономичностью  и  простотой  возведения  в  условиях  мирового  кризиса  и  международных  санкций  против  РФ.

Список  литературы:

1.Ермолов  В.В.  Воздухоопорные  здания  и  сооружения.  М.:  Стройиздат,  1980.  —  304  с.

2.Ким  А.Ю.  Численное  исследование  нелинейных  мембранно-пневматических  систем.  СГАУ,  Саратов,  2001.  —  263  с.  Монография  депонирована  в  ВИНИТИ  РАН  28.04.01  №  1122  —  В2001.