МЕТОД  ПОПОЛНЕНИЯ  ОБУЧАЮЩЕЙ  ВЫБОРКИ  ИНС  ДЛЯ  БИОМЕТРИЧЕСКИХ  ПАРАМЕТРОВ  МЕТОДОМ  ВЫПУКЛЫХ  ОБОЛОЧЕК

Еловский  Дмитрий  Александрович

ведущий  инженер,  ЗАО  «Связь-Инжиниринг»,  РФ,  г.  Москва

E-mail:  dmitry.elovsky@gmail.com

GAINING  TRAINING  SAMPLE  FOR  ANN  FOR  BIOMETRIC  PARAMETERS  BASED  ON  CONVEX  HULL

Elovsky  Dmitry

lead  Engineer ,  CJSC  Svyaz  engineering,  Russia,  Moscow

Аннотация

В  статье  описывается  метод  пополнения  обучающей  выборки  искусственной  нейронной  сети  для  идентификации  биометрических  образов,  основанный  на  использовании  выпуклых  оболочек.  Приведено  описание  метода  и  сравнение  с  подобным  методом  параллелепипеда.

ABSTRACT

The  article  describes  the  method  of  gaining  training  sample  for  artificial  neural  network  for  biometric  identification,  based  on  using  convex  hulls.  A  description  of  the  method  and  its  comparison  with  a  similar  box  method  are  reported.

Ключевые  слова :  нейронные  сети;  выборка;  выпуклые  оболочки.

Keywords :  artificial  neuron  network;  training  sample;  convex  hull.

Введение

Большинство  современных  способов  идентификации  и  аутентификации  личности  используют  алгоритмы  нечёткой  логики,  в  частности,  нейронные  сети  [1;  2].  Последние  требуют  для  корректной  работы  наличие  набора  обучающих  данных  —  обучающую  выборку  —  некоторый  набор  входных  образов  для  обучения  сети.  Входные  образы  для  нейронных  сетей,  решающих  задачи  подобного  класса,  имеют  размерность  больше  20,  что  влечёт  за  собой  необходимость  большого  объёма  данных  для  обучения.  Налицо  проблема  формирования  этой  самой  обучающей  выборки.  Распространён  подход,  при  котором  в  процессе  работы  сети,  правильно  классифицированные  образы  добавляются  к  обучающим,  и  через  какое-то  время  сеть  снова  обучают  уже  на  новом,  пополненном  наборе  входных  образов.  Это  снижает  ошибки  первого  и  второго  рода  в  процессе  работы  сети,  однако  на  начальном  этапе  недостаточность  выборки  приводит  к  большому  проценту  ошибок  обоих  родов,  причём  второго  (идентификация  не  зарегистрированного  пользователя)  критичнее,  чем  первого. 

Задача  идентификации/аутентификации

Задача  идентификации/аутентификации  по  сути  является  задачей  классификации:  определения  принадлежности  входного  вектора  к  одному  из  двух  классов:  «свой»  и  «чужой».  Компонентами  входного  n-мерного  вектора  для  подобных  сетей  являются  значения  биометрических  показателей,  распределённых  нормально  [2].  Вследствие  этого,  векторы  в  n-мерном  пространстве  образуют  некоторый  гиперэллипсоид  рассеивания.  Для  данного  гиперэллипсоида  можно  указать  «границу  доверия»,  т.  е.  область,  внутри  которой  находятся  образы  с  достаточной  вероятностью  принадлежащие  классу  «свой».  Образы,  находящиеся  за  его  пределами,  имеют  среднеквадратичное  отклонение  больше  заданного,  и  не  принадлежат  данному  классу,  по  крайней  мере,  на  первом  этапе  обучения  сети. 

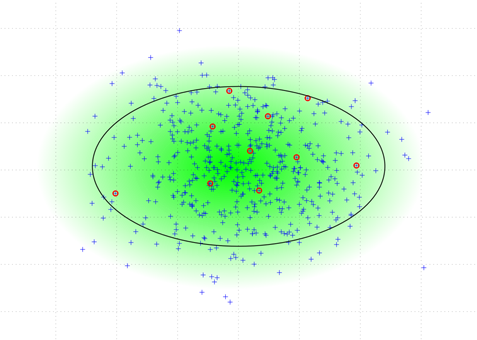
Рисунок  1.  Гиперэллипсоид  рассеивания  и  «граница  доверия»

Рассмотрим  два  метода  получения  обучающих  образов:  параллелепипеда  и  выпуклых  оболочек.  Для  простоты  рассмотрим  случай  с  двумя  биометрическими  показателями,  выводы  без  труда  распространяются  и  на  пространства  больших  размерностей.  Возьмём  готовый  набор  ,  состоящий  из    образов  (на  рисунках  будем  обозначать  их  маркерами  «+»).  Это  полный  набор  образов,  т.  е.  это  —  все  образы,  полученные  в  процессе  работы  сети.  Выберем    случайных  образов  из  ,  которые  будут  составлять  исходную  обучающую  выборку    (обозначим  её  элементы  маркерами  «○»).  На  рисунке  1  изображены  элементы    и  .  Градиентом  показан  эллипсоид  рассеивания,  а  границей  эллипса  —  граница  «области  доверия».

Метод  параллелепипеда

Данный  метод  является  наиболее  простым  способом  получения  новых  входных  образов.  Метод  заключается  в  следующем:  в  выборку  включают  точки,  лежащие  внутри  гиперпараллелепипеда,  описывающего  «границу  доверия».  Рёбра  гиперпараллелепипеда  параллельны  осям  координат.  Так  как  «граница  доверия»  априори  не  известна,  то  гиперпараллелепипед  строится  так,  что  каждая  из  его  граней  содержит  хотя  бы  одну  точку  из  ,  а  все  точки  из  ,  не  лежащие  на  гранях,  лежат  внутри  этого  гиперпараллелепипеда.  На  рисунке  2  показано  построение  гиперпараллелепипеда  для  двумерного  случая.

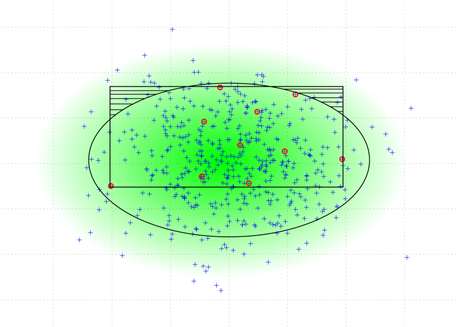
Рисунок  2.  Получение  репрезентативной  выборки  методом  параллелограмма

Заштрихованные  линии  на  рисунке  2  —  области  ошибки  второго  рода.  Очевидно,  что  ошибка  второго  рода  отсутствует  только  в  том  случае,  когда  гиперпараллелепипед  полностью  содержится  в  «области  доверия». 

Видно,  что  ошибка  второго  рода  тем  больше,  чем  больше  среднеквадратическое  отклонение    образов  исходной  обучающей  выборки  .  Т.  о.  область,  ограниченная  гиперпараллелепипедом  содержит  области  не  принадлежащие  «области  доверия».  Область,  принадлежащая  «области  доверия»,  но  не  принадлежащая  гиперпараллелепипеду  —  область  ошибок  первого  рода.  На  практике  ошибки  первого  рода  менее  критичны,  тем  боле,  что  их  относительное  количество  уменьшается  в  процессе  работы  сети.

Метод  выпуклых  оболочек

Воспользуемся  одним  из  алгоритмов  [3]  и  построим  на  образах    выпуклую  оболочку  (см.  рисунок  3).  Мы  получили  систему    гиперплоскостей,  ограничивающих  область,  содержащую  все  .  Любую  точку  из  этой  области  можно  добавить  к    для  расширения  обучающей  выборки.  Из  рисунка  3  видно,  что  ошибка  второго  рода  отсутствует.  В  частности,  она  появляется  только  тогда,  когда  выборка    содержит  случайные  выбросы,  которые  находятся  за  пределами  «области  доверия».  Случайные  выбросы  легко  ликвидируются  статистическими  методами.

Рисунок  3.  Получение  репрезентативной  выборки  методом  выпуклых  оболочек

Найдём  математический  центр    —  математическое  ожидание  области  .  Очевидно,  что    есть  центр  гиперэллипса,  к  которому  будет  стремиться  математическое  ожидание    образов  при  .  Если  все  образы    из    лежат  в  «области  доверия»,  то  расстояние  от  каждого  из  них  до  центра    не  превосходит  радиуса  гиперэллипса,  лежащего  на  прямой  .  Нужно  показать,  что  расстояние  между  любой  точкой,  лежащей  на  грани/ребре    и  центром    не  превосходит  соответствующих  радиусов.  Действительно,  точки  ,  образующие  ,  лежат  в  выпуклой  области  .  Из  выпуклости    следует,  что  все  точки    так  же  принадлежат  ,  следовательно,  точки,  принадлежащие  выпуклой  оболочке  также  принадлежат  .

Ошибки  второго  рода

Выше  было  показано,  что  для  метода  выпуклых  оболочек  ошибка  второго  рода  меньше  при  условии,  что  все    лежат  внутри  «области  доверия».  Покажем  теперь,  что  ошибка  меньше  и  в  случае  случайных  выбросов.  Этот  очевидный  факт  легче  всего  продемонстрировать  геометрически  (см.  рисунок  4).  Рассмотрим  один  и  тот  же  набор  образов,  и  допустим,  что  один  из  них  —  случайный  выброс.

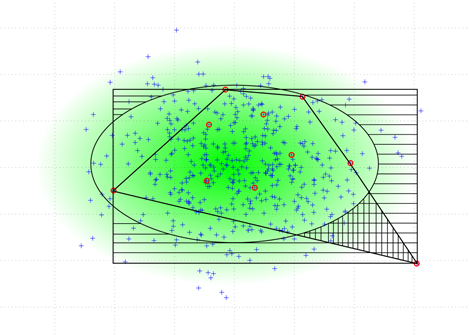
Рисунок  4.  Ошибки  второго  рода  обоих  методов

На  рисунке  горизонтальная  и  вертикальная  штриховки  —  ошибки  второго  рода  методов  параллелепипеда  и  выпуклых  оболочек  соответственно.  Область,  имеющая  только  горизонтальную  штриховку  есть  разница  ошибок  обоих  методов,  т.  е.  область  ошибки  второго  рода  метода  выпуклых  оболочек  содержится  в  аналогичной  области  метода  параллелограмма.  Области  будут  совпадать  только  в  том  случае,  если  все  вершины  гиперраллелепипеда  будут  внешними  точками  выпуклой  оболочки,  а  все  остальные  точки  лежат  внутри  области  гиперраллелепипеда. 

Таким  образом,  даже  если  выборка    содержит  случайные  выбросы,  ошибка  второго  рода  в  методе  выпуклых  оболочек  меньше,  чем  в  методе  параллелепипеда.

Модификация  алгоритма  выпуклых  оболочек 

Сложность  построения  выпуклой  оболочки  растёт  с  ростом  размерности  пространства  и  количества  точек  для  построения.  Это  следует  хотя  бы  из  того,  что  в  n-мерном  пространстве  в  качестве  граней  рассматриваются  гиперплоскости.  Так  же  стоит  помнить  о  том,  что  в  пространстве    минимальное  число  точек  для  построения  равно    (это  минимальное  количество  точек,  необходимых  для  построения  выпуклого  тела  в  пространстве  ). 

Из  пространства  параметров    можно  исключить    параметров  с  малым  ,  приняв  соответствующие  координаты  образов  за  их  математическое  ожидание.  Действительно,  при  малом  среднеквадратическом  отклонении,  параметры  принимают  значения  близкие  к  их  среднему  и  не  вносят  большого  вклада  в  объём  «области  доверия».  И  наоборот,  параметры  с  бо́льшим    вносят  больше  в  объём  .  Теперь  в  алгоритме  участвуют    параметров.  Рассмотрим  случай  с  тремя  параметрами,  т.  е.    (см.  рисунок  5).  Исходная  выборка  практически  лежит  в  некоторой  плоскости,  параллельной  одной  из  координатных  осей.  Исключив  соответствующий  параметр  из  рассмотрения  (в  данном  случае  )  мы  приходим  к  двумерному  (т.  е.  )  случаю. 

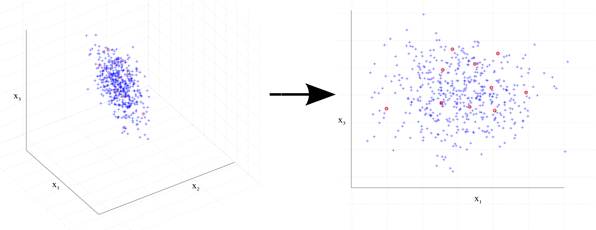
Рисунок  5.  Уменьшение  размерности  входного  пространства

Выводы

Оба  рассмотренных  метода  основаны  на  предположении  о  нормальном  распределении  параметров  и,  следовательно,  выпуклости  множества  входных  образов  и  в  общем  случае  не  применимы  для  произвольно  распределенных  векторов.  Метод  выпуклых  оболочек  даёт  большую  вероятность  ошибок  первого  рода,  но  меньшую  второго,  что  делает  его  использование  более  предпочтительным.  Однако  вычислительная  сложность  построения  выпуклой  оболочки  растёт  много  быстрее  с  ростом  размерности  входного  пространства  и  ростом  количества  точек,  и  как  следствие,  растёт  сложность  метода  в  целом.  В  связи  с  этим  целесообразно  применять  метод  для  параметров  имеющих  наибольшую  дисперсию,  приравнивая  остальные  к  их  средним  значениям.  Кроме  того,  с  ростом  количества  образов  исходной  выборки,  выпуклая  оболочка  приближается  к  «границе  доверия»,  тогда  при  неоправданно  огромных  вычислительных  и  как  следствие  временных  затратах  получение  репрезентативной  выборки  есть  ни  что  иное  как  работа  нейронной  сети,  что  негативно  сказывается  на  производительности.

Список  литературы:

1.Брюхомицкий  Ю.А.  Классификация  биометрических  параметров  пользователя  с  помощью  вероятностных  методов  //  Известия  ЮФУ.  Технические  науки.  2005.  №  4. 

2.Брюхомицкий  Ю.А.  Биометрическая  аутентификация  на  основе  вероятностной  нейронной  сети  //  Известия  ЮФУ.  Технические  науки.  —  2004.  —  №  1.  —  С.  88.

3.Ивантер  Э.В.,  Коросов  А.В.  И  228  Элементарная  биометрия  :  учеб.  пособие  /  Э.В.  Ивантер,  А.В.  Коросов.  –Петрозаводск:  Изд-во  ПетрГУ,  2010.  ––  104  с.  ISBN  978-5-8021-1112-3.

4.Кормен,  Томас  Х.,  Лейзерсон,  Чарльз  И.,  Ривест,  Рональд  Л.,  Штайн,  Клифорд.  Вычислительная  геометрия  //  Алгоритмы:  построение  и  анализ.  М.:  «Вильямс»,  2005.  —  ISBN  5-8459-0857-4.