КОЛЕБАНИЯ  ЦИЛИНДРИЧЕСКОЙ  КАПЛИ  В  ПЕРЕМЕННОМ  ЭЛЕКТРИЧЕСКОМ  ПОЛЕ

Алабужев  Алексей  Анатольевич

канд.  физ.-мат.  наук,  с.н.с.  лаборатории  Вычислительной  гидродинамики,  Института  Механики  сплошных  сред  УрО  РАН,  РФ,  г.  Пермь

E -mail:  alabuzhev@mail.ru

Кашина  Марина  Анатольевна

студент  2  курса  физического  факультета  Пермского  национального  исследовательского  университета,  РФ,  г.  Пермь

E-mail: 

PARAMETRICAL  INSTABILITY  OF  CYLINDRICAL  DROP  IN  ALTERNATING  ELECTRIC  FIELD

Aleksey  Alabuzhev

candidate  of  Science,  Senior  staff  scientist  of  Laboratory  of  Computational  Hydrodynamics,  Institute  of  Continuous  Media  Mechanics  UB  RAS,  Russia,  Perm

Marina  Kashina

student  of  Physical  Department,  Perm  State  University,  Russia,  Perm

Работа  поддержана  РФФИ  (грант  №  14-01-96017-р-урал-а).

АННОТАЦИЯ

В  данной  работе  исследуется  поведение  капли  несжимаемой  жидкости  под  действием  переменного  электрического  поля.  В  равновесном  состоянии  капля  имеет  форму  цилиндра,  ограниченного  в  осевом  направлении  параллельными  твердыми  плоскостями.  Электрическое  поле  периодично  по  времени  с  некоторой  частотой.  Рассмотрены  вынужденные  колебания  капли.  Получены  данные  об  отклонении  поверхности  и  частотных  характеристиках  в  зависимости  от  параметров  задачи.

ABSTRACT

The  behavior  of  a  drop  of  incompressible  fluid  under  the  influence  of  an  alternating  electric  field  is  investigated  in  this  paper.  In  equilibrium,  the  drop  is  cylindrical,  limited  axially  parallel  solid  planes.  The  electric  field  is  periodic  in  time  with  a  certain  frequency.  The  forced  oscillations  of  the  drop  considered.  The  surface  deviation  and  frequency  characteristics  depending  on  the  parameters  of  the  problem  were  obtained.

Ключевые  слова:  капля  жидкости;  линейный  резонанс;  переменное  электрическое  поле;  вынужденные  колебания;  электросмачивание.

Keywords:  fluid  drop,  linear  resonance,  alternating  electric  field,  power  oscillations,  electrowetting.

1.  Постановка  задачи

Капля  несжимаемой  жидкости  с  плотностью  ,  окруженная  другой  жидкостью  плотности  .  Вся  система  ограничена  двумя  параллельными  твердыми  поверхностями  (рис.  1),  расстояние  между  которыми  равно  .  Сосуд  замкнут  на  бесконечности.  Капля  имеет  форму  цилиндра  радиусом    в  отсутствие  внешних  сил.  Равновесный  краевой  угол  между  боковой  поверхностью  капли  и  твердыми  плоскостями  прямой.  На  систему  действует  переменной  неоднородное  электрическое  поле  с  амплитудой    и  частотой  .  Это  поле  играет  роль  внешней  силы,  которая  заставляет  двигаться  контактную  линию.  Для  описания  движения  контактной  линии  используется  модифицированное  условие  Хокинга  [3]:  скорость  движения  контактной  линии  пропорциональна  сумме  отклонения  краевого  угла  и  скорости  быстрых  релаксационных  процессов,  частоты  которых  пропорциональная  удвоенной  частоте  электрического  поля  .

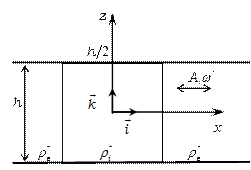
Рисунок  1.  Геометрия  задачи

Выберем  в  качестве  единиц  измерения  времени  ,  радиальной  координаты  ,  осевой  координаты  ,  отклонения  поверхности  ,  скорости  ,  плотности  ,  давления  ,  где    –  коэффициент  поверхностного  натяжения.

В  пренебрежении  вязким  затуханием  запишем  в  безразмерной  форме  уравнения  Бернулли  и  непрерывности  и  граничных  условий:

                                        ,  ,                                       

:           ,  ,  ,                   

,  :       ,                                 

:                                  ,                                                  

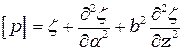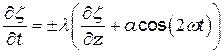где  квадратные  скобки  обозначают  скачок  величины  на  границе  раздела  между  внешней  жидкостью  и  каплей,    —  потенциал  скорости,    —  отклонение  поверхности  от  равновесного  положения,    —  безразмерная  постоянная  Хокинга.  Отметим,  что  постоянная  Хокинга  в  условии    имеет  два  важных  предельных  случая:    —  закрепленная  линия  контакта,    –  свободно  скользящая  контактная  линия. 

Краевая  задача  —  содержит  шесть  безразмерных  параметров:  малую  относительную  характерную  амплитуду  ,  постоянную  Хокинга  (параметр  смачивания)  ,  частоту  внешнего  воздействия  ,  геометрический  параметр  ,  плотность  внешней  жидкости  ,  плотность  жидкости  в  капле  ,  последние  два  параметра  связаны  соотношением  .

2.  ВЫНУЖДЕННЫЕ  КОЛЕБАНИЯ

Собственные  колебания  такой  капли  были  изучены  в  работе  [1].  Нечетные  моды  вынужденных  колебаний  исследовались  в  [2].  Решение  уравнения  Лапласа    с  учетом  граничного  условия    можно  записать  в  виде:

                      ,                     

                       ,                      

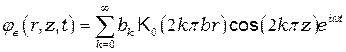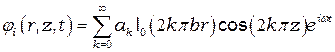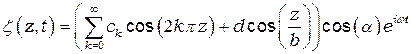
где  ,    —  модифицированные  функции  Бесселя.  Подставляя  решения  —  в  уравнения  —,  получим  выражения  для  неизвестных  амплитуд  ,  ,    и  . 

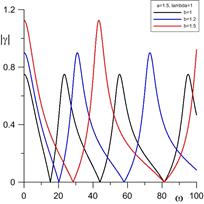
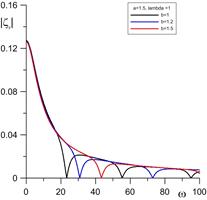
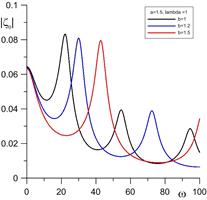
Рисунок  2.  Максимальное  отклонение  боковой  поверхности  и  краевого  угла  при  трех  разных  значениях  b   (,  ,  ).

На  рис.  2  показано  максимальное  отклонение  боковой  поверхности  на  верхней  подложке  ,  в  середине  слоя    и  значения  краевого  угла  :    в  зависимости  от  частоты  электрического  поля  при  разных  значениях  геометрического  параметра  .

На  рис.  3  показано  максимальное  отклонение  боковой  поверхности  на  верхней  подложке  ,  в  середине  слоя    и  значения  краевого  угла  :    в  зависимости  от  частоты  электрического  поля  при  разных  значениях  постоянной  Хокинга  .

Сравнивая  полученные  зависимости  с  результатами  натурных  экспериментов  можно  определить  постоянную  Хокинга  .

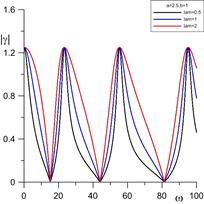
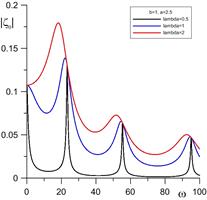
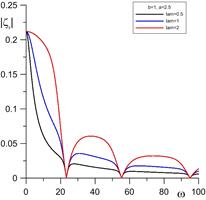
Рисунок  3.  Максимальное  отклонение  боковой  поверхности  и  краевого  угла  при  трех  разных  значениях    (,  ,  ).

Список  литературы:

1.Алабужев  А.А.,  Любимов  Д.В.  Влияние  динамики  контактной  линии  на  собственные  колебания  цилиндрической  капли  //  ПМТФ.  —  2007.  —  Т.  48,  №  5.  —  С.  78—86.

2.Кашина  М.А.  Влияние  переменного  электрического  поля  на  колебания  цилиндрической  капли  //  Материалы  XXIII  Всероссийской  школы-конференции  молодых  ученых  и  студентов  «Математическое  моделирование  в  естественных  науках».  Изд-во  ПНИПУ,  г.  Пермь,  2014.  —  С.  120—122.

3.Hocking  L.M.  The  damping  of  capillary-gravity  waves  at  a  rigid  boundary  //  J.  Fluid  Mech.  —  1987.  —  V.  179.  —  P.  253—266.