МЕТОД  КОНФИГУРАЦИОННЫХ  ФУНКЦИЙ  В  ОПИСАНИИ  ПРОЦЕССОВ  ФОРМИРОВАНИЯ  АППАРАТНЫХ  УРОВНЕЙ  РЕКОНФИГУРИРУЕМОЙ  СИСТЕМЫ  КОНТРОЛЯ  И  ДИАГНОСТИКИ  КОСМИЧЕСКОГО  АППАРАТА

Савкин  Леонид  Васильевич

аспирант  ФГУП  «НПО  им.  С.А.  Лавочкина»,  начальник  бюро  Филиала  ФГУП  «НПО  им.  С.А.  Лавочкина»,  РФ,  г.  Калуга

E-mail: 

THE  METHOD  OF  CONFIGURATION  FUNCTIONS  IN  THE  DESCRIPTION  OF  PROCESSES  FORMATION  THE  HARDWARE  LEVELS  OF  THE  RECONFIGURABLE  SYSTEM  MONITORING  AND  DIAGNOSTICS  OF  THE  SPACECRAFT

Leonid  Savkin

graduate  student,  chief  of  bureau,  The  Branch  of  Federal  Enterprise  “Lavochkin  Association”,  Russia,  Kaluga

АННОТАЦИЯ

Предложен  способ  математической  формализации  процессов  формирования  диагностической  модели  в  реконфигурируемой  системе  контроля  и  диагностики  космического  аппарата.  Показан  процесс  формирования  аппаратных  уровней  диагностической  модели.  Получена  система  уравнений,  описывающая  диагностическую  модель  с  точки  зрения  топологии  связей  между  ее  элементами  и  функций  данных  элементов.

ABSTRACT

The  method  of  mathematical  formalization  of  the  processes  formation  diagnostic  model  in  the  reconfigurable  system  monitoring  and  diagnostics  of  the  spacecraft  is  offered.  Process  of  formation  of  the  hardware  levels  of  diagnostic  model  is  shown.  The  system  of  equations  describing  diagnostic  model  on  the  basis  topology  of  communications  between  its  elements  and  on  the  basis  functions  of  these  elements  is  received.

Ключевые  слова:  конфигурационная  функция;  диагностическая  модель;  многоуровневая  реконфигурация;  топология;  логико-арифметическая  связь.

Keywords:  configuration  function;  diagnostic  model;  multi-level  reconfiguration;  topology;  logic  arithmetical  communication.

В  предыдущих  работах  [8—10]  рассматривались  принципы  организации  бортового  диагностического  обеспечения  космических  аппаратов  (КА)  на  базе  реконфигурируемых  вычислительных  систем  (РВС).  В  качестве  основного  аргумента,  выдвигаемого  на  обоснование  преимуществ  реконфигурируемой  системы  контроля  и  диагностики  (СКД),  построенной  на  базе  РВС,  перед  СКД,  реализованными  программными  средствами,  была  представлена  возможность  глубокого  перестроения  диагностической  модели  в  процессе  идентификации  неисправностей  и  отказов  сложного  типа. 

Построение  диагностической  модели  в  реконфигурируемом  вычислительном  поле  (РВП)  предлагалось  осуществлять  по  принципу  сложной  иерархической  системы,  обладающей  возможностью  реконфигурации  функциональных  элементов,  которые  бы  участвовали  в  формировании  всех  ее  аппаратных  уровней,  что,  в  свою  очередь,  наделило  бы  систему  возможностью  многоуровневой  реконфигурации.  Данная  возможность  обеспечила  бы  СКД  КА  возможностью  кардинального  перестроения  диагностической  модели  в  процессе  выбора  наиболее  эффективных  алгоритмов  диагностики  и  контроля,  адаптируя  тем  самым  всю  аппаратную  структуру  СКД  под  информационную  структуру  задач  бортового  диагностирования.  Данное  свойство  является  особенно  актуальным  ввиду  как  непрерывного  роста  сложности  аппаратно-программного  построения  бортовых  систем  современных  КА,  так  и  ввиду  соответствующего  усложнения  алгоритмов  идентификации  состояний  данных  систем  с  заданной  степенью  достоверности.

В  [10]  было  предложено  строить  диагностическую  модель  по  принципу  вложенных  матричных  структур  не  зависимо  от  того,  какой  бы  степенью  сложности  (в  структурном  отношении)  она  обладала  на  самом  высоком  аппаратном  уровне.

Сам  принцип  формирования  аппаратных  уровней  диагностической  модели  представлен  на  рисунке  1,  где  показано,  что  каждый  элемент  -го  аппаратного  уровня  образуется  путем  строго  заданной  топологии  параллельно-последовательных  логико-арифметических  связей  между  функциональными  элементами  -го  аппаратного  уровня,  где    —  порядковый  номер  аппаратного  уровня  диагностической  модели,  образованной  в  РВП  СКД  КА.

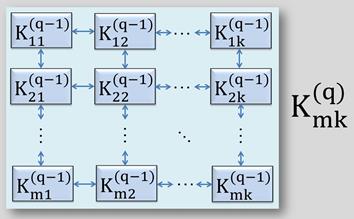
Рисунок  1.  Принцип  формирования  аппаратных  уровней  диагностической  модели  в  реконфигурируемой  СКД  КА

Из  данного  рисунка  следует,  что  каждый  из  аппаратных  уровней  диагностической  модели  формируется  независимо,  начиная  от  первого  аппаратного  уровня  ,  и  заканчивая  последним  аппаратным  уровнем  .

На  рисунке  2  показан  процесс  формирования  уровней  аппаратной  конфигурации  диагностической  модели  в  РВП  в  зависимости  от  конфигурационной  функции  ,  которая  должна  учитывать  топологию  логико-арифметических  связей  диагностической  модели  на  каждом  из  образующих  ее  аппаратных  уровней.

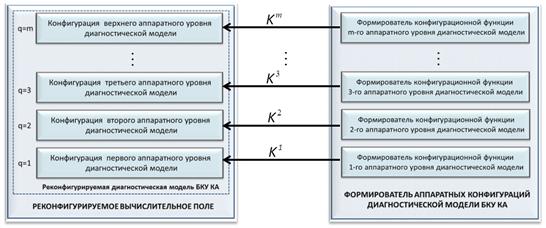
Рисунок  2.  Формирование  уровней  аппаратной  конфигурации  диагностической  модели  в  зависимости  от  конфигурационной  функции  K ^(q)

Однако,  не  смотря  на  то,  что  данный  рисунок  иллюстрирует  процесс  формирования  конфигурационных  функций  в  независимых  формирователях,  это  вовсе  не  означает,  что  можно  построить  диагностическую  модель  с  многоуровневой  реконфигурацией,  не  учитывая  при  этом  конфигурационные  функции  ее  отдельных  аппаратных  уровней.  Интуитивно  понятно,  что  такое  в  принципе  не  может  быть,  поскольку  каждые  последующие  аппаратные  уровни  диагностической  модели  образуются  за  счет  комбинаций  и  топологических  связей  между  функциональными  элементами  предыдущих  аппаратных  уровней,  что  можно  записать  в  виде  рекуррентного  соотношения

,  (1)

где:    —  конфигурационная  функция  -го  аппаратного  уровня  диагностической  модели; 

  —  матрица  логико-арифметических  функций,  реализуемых  посредством  коммутируемых  логических  блоков  (КЛБ),  не  учитывающая  топологию  их  логико-арифметических  связей  внутри  РВП; 

  —  орграф  логико-арифметических  связей  между  функциональными  элементами  -го  аппаратного  уровня  диагностической  модели,  которые  образуют  элемент  -го  аппаратного  уровня.

Для  более  наглядного  представления  об  аргументах  и    функции    рассмотрим  рисунок  3,  на  котором  представлен  участок  РВП,  образованный  матричным  набором  КЛБ.

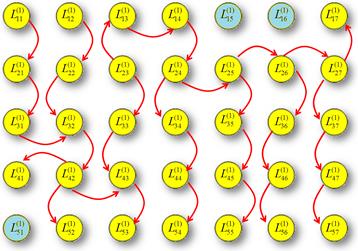
Рисунок  3.  Параллельно-последовательная  топология  логико-арифметических  связей  внутри  элемента  второго  аппаратного  уровня  диагностической  модели

Здесь  посредством  КЛБ  реализуется  определенная  базовая  логико-арифметическая  операция  ,  поэтому  матрица  представляет  собой  набор  логико-арифметических  функций  реализуемых  посредством  КЛБ,  которые  расположены  в  строке  матрицы  РВП    и  в  столбце  матрицы  РВП  .  Представить  математически  данную  матрицу  можно  в  следующем  виде:

,

где  коэффициент  есть  функция  включения  (задействования)  КЛБ  в  образовании  элемента  второго  аппаратного  уровня,  т.  е. 

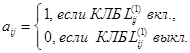  (2)

Матрицу  логико-арифметических  функций  для  данного  рисунка  можно  записать  в  виде

,  (3)

а,  учитывая,  что  элементы  (КЛБ)    и    не  задействованы,  и,  принимая  во  внимание  (2),  получим

.  (4)

Для  матриц  (3)  и  (4)  необходимо  отметить  следующее.  Ввиду  того,  что  логико-арифметическая  функция  КЛБ  может  быть  отключена  как  функционально,  так  и  топологически  (т.  е.  находиться  во  включенном  состоянии,  но  быть  незадействованной  в  вычислительном  процессе),  то  коэффициент  должен  присутствовать  как  в  матрице  базового  аппаратного  уровня  КЛБ  в  РВП,  так  и  в  матрицах  конфигурационных  функций.  Это  связано  с  тем,  что  в  процессе  формирования  диагностической  модели  или  ее  реконфигурации,  могут  отключаться  функциональные  элементы  не  только  первого  аппаратного  уровня,  но  и  элементы  более  высоких  аппаратных  уровней  .

Поэтому  для  различных  ситуаций  матрица  может  быть  записана  либо  в  виде  выражения  (3),  либо  в  виде  выражения  (4).

Из  рисунка  3  также  видно,  что  функциональное  назначение  элемента  второго  аппаратного  уровня  зависит  от  параллельно-последовательной  топологии  логико-арифметических  связей.  Именно  поэтому  орграф  необходимо  включать  как  аргумент  конфигурационной  функции  ,  начиная  со  второго  аппаратного  уровня,  которому  будет  соответствовать  конфигурационная  функция 

,

  —  орграф  логико-арифметических  связей  между  функциональными  элементами  первого  аппаратного  уровня,  в  качестве  которых  выступают  КЛБ,  причем  в  данном  случае

.

На  рисунке  4  показано,  что  процесс  образования  элемента  второго  аппаратного  уровня  есть  не  что  иное,  как  обычное  выделение  фрагмента  РВП  с  минимально  необходимым  набором  КЛБ.

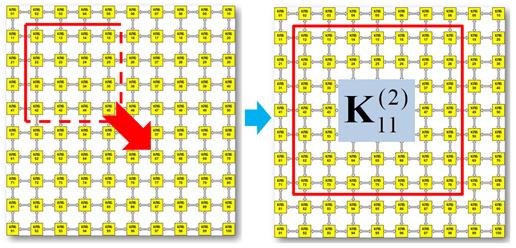
Рисунок  4.  Выделение  из  РВП  функционального  элемента  второго  аппаратного  уровня  диагностической  модели

При  этом,  в  некоторых  случаях  элемент  второго  аппаратного  уровня  может  быть  образован  не  только  в  виде  квадратичного  набора  ,  но  также  и  в  виде  строки  или  столбца.

Продолжая  использовать  принцип  вложенных  матричных  наборов  в  образовании  функциональных  элементов  более  высоких  аппаратных  уровней  диагностической  модели,  рассмотрим  рисунок  5.

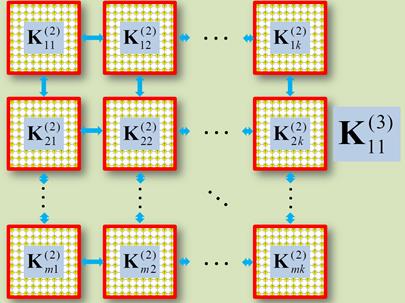
Рисунок  5.  Формирование  элемента  третьего  аппаратного  уровня  диагностической  модели

Здесь  показано,  что  элемент  третьего  аппаратного  уровня  диагностической  модели,  образуется  на  базе  матрицы  элементов  второго  аппаратного  уровня,  что  исходя  из  (1)  можно  представить  соответствующей  конфигурационной  функцией  третьего  аппаратного  уровня  вида

,

где    —  орграф  логико-арифметических  связей  между  функциональными  элементами  второго  аппаратного  уровня,  образующими  элемент  третьего  аппаратного  уровня.

Из  рисунка  5  становится  понятно,  что  конфигурационная  функция  аппаратного  уровня  также  представляет  собой  матрицу  вида

,

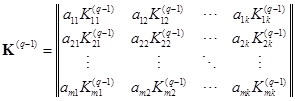где  элемент    —  является  уже  логико-арифметической  функцией  элемента  -го  аппаратного  уровня  диагностической  модели; 

коэффициент  —  функция  включения  функционального  элемента  -го  аппаратного  уровня.

Аналогичным  образом  происходит  формирование  элементов  более  высоких  аппаратных  уровней  (рисунок  6).

Рисунок  6.  Формирование  элемента  четвертого  аппаратного  уровня  диагностической  модели

Исходя  из  всего  вышесказанного,  необходимо  отметить,  что  поскольку  конфигурационные  функции  описывают  все  особенности  структуры  диагностической  модели,  причем  как  вычислительную  структуру,  так  и  топологию  логико-арифметических  связей,  то  для  полного  описания  диагностической  модели,  построенной  по  предложенному  принципу,  достаточно  использовать  систему  уравнений  вида

  (5)

где    —  система  конфигурационных  функций,  образующих  диагностическую  модель  с  возможностью  многоуровневой  реконфигурации. 

Таким  образом,  выражение  (5)  полностью  описывает  диагностическую  модель,  формируемую  в  реконфигурируемой  СКД  КА,  включая  при  этом  как  базовый  уровень  РВП,  так  и  структурную  организацию  диагностической  модели  на  всех  этапах  ее  формирования.

Выводы:

1.  Предложен  способ  математической  формализации  процесса  формирования  диагностической  модели  по  принципу  вложенных  матричных  структур,  с  возможностью  многоуровневой  реконфигурации  функциональных  элементов  за  счет  перераспределения  топологии  логико-арифметических  связей  на  всех  аппаратных  уровнях  диагностической  модели.

2.  Детально  рассмотрены  принципы  формирования  диагностической  модели  в  РВП,  учитывающие  следующие  основные  характеристики  диагностической  модели:

·     базовые  логико-арифметические  функции,  реализуемые  за  счет  КЛБ;

·     логико-арифметические  функции  элементов  аппаратных  уровней  ;

·     структуру  и  способы  организации  аппаратных  уровней  диагностической  модели;

·     топологию  логико-арифметических  связей  на  каждом  из  аппаратных  уровней  диагностической  модели;

·     возможности  реконфигурации  диагностической  модели  на  каждом  из  ее  аппаратных  уровней.

3.  Получена  система  уравнений,  описывающая  диагностическую  модель  в  РВП  реконфигурируемой  СКД  КА  на  всех  стадиях  формирования  ее  аппаратных  уровней.  Данная  система  уравнений  учитывает  особенности  диагностической  модели  как  на  базовом  логико-арифметическом  уровне  КЛБ,  так  и  на  топологическом  уровне,  включающем  в  себя  описание  всех  типов  логико-арифметических  связей  между  функциональными  элементами  диагностической  модели  с  образованием  новых  на  каждом  из  формируемых  аппаратных  уровней.

Список  литературы:

1.Алексеев  А.А.,  Кораблев  Ю.А.,  Шестопалов  М.Ю.  Идентификация  и  диагностика  систем.  М.:  Издательский  центр  «Академия»,  2009.  —  352  с.

2.Бровкин  А.Г.,  Бурдыгов  Б.Г.,  Гордийко  С.В.  и  др.  Бортовые  системы  управления  космическими  аппаратами.  /Под  ред.  проф.  А.С.  Сырова  М.:  Изд-во  МАИ-ПРИНТ,  2010.  —  304  с.

3.Глущенко  П.В.  Техническая  диагностика:  Моделирование  в  диагностировании  и  прогнозировании  состояния  технических  объектов.  М.:  Вузовская  книга,  2004.  —  248  с.

4.Евреинов  Э.В.  Однородные  вычислительные  системы,  структуры  и  среды.  М.:  Радио  и  связь,  1981.  —  208  с.

5.Евреинов  Э.В.,  Хорошевский  В.Г.  Однородные  вычислительные  системы.-Новосибирск:  Наука,  1978.

6.Каляев  А.В.  Многопроцессорные  системы  с  программируемой  архитектурой.  М.:  Радио  и  связь,  1984,  —  240  с.

7.Каляев  И.А.,  Левин  И.И.,  Семерников  Е.А.,  Шмойлов  В.И.  Реконфигурируемые  мультиконвейерные  вычислительные  структуры  /Изд.  2-е,  перераб.  и  доп.  /  Под  общ.  Ред.  И.А.  Каляева.  Ростов-н/Д.:  Изд-во  ЮНЦ  РАН,  2009.  —  344  с.

8.Савкин  Л.В.  О  решении  задач  бортового  диагностирования  космических  аппаратов  с  помощью  реконфигурируемых  вычислительных  систем.  Технические  науки  —  от  теории  к  практике  /  Сб.  ст.  по  материалам  XXXIX  Междунар.  науч.-практ.  конф.  №  10  (35).  Новосибирск:  Изд.  «СибАК»,  2014.  —  с.  79—87.

9.Савкин  Л.В.,  Клочко  О.С.,  Макаров  А.С.  Реализация  алгоритмов  распознавания  сложных  видов  неисправностей  и  отказов  бортовой  аппаратуры  космических  аппаратов  на  основе  встроенных  реконфигурируемых  диагностических  систем  //  Universum:  Технические  науки  :  электрон.  научн.  журн.  2014.  №  11  (12)  .  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://7universum.com/ru/tech/archive/item/1756  (дата  обращения:  23.12.2014).

10.Савкин  Л.В.,  Новичков  В.М.,  Ширшаков  А.Е.  Многоуровневая  реконфигурация  моделей  диагностических  систем  как  средство  повышения  гибкости  алгоритмов  диагностики  и  контроля  бортовых  систем  космических  аппаратов.  Наукоемкие  технологии  в  приборо-  и  машиностроении  и  развитие  инновационной  деятельности  в  вузе:  материалы  Всероссийской  научно-технической  конференции,  25—27  ноября  2014  г.  Т.  2.  М.:  Издательство  МГТУ  им.  Н.Э.  Баумана,  2014.  —  С.  296—299.