Статья опубликована в рамках: XL Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 19 ноября 2014 г.)
Наука: Технические науки
Секция: Строительство и архитектура
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ЗАДАЧА УСТОЙЧИВОСТИ РАМЫ В РАМКАХ ТЕОРИИ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ
Шляхов Станислав Михайлович
д-р физ.-мат. наук, профессор Саратовского государственного технического университета, РФ, г. Саратов
Кривулина Эльвира Федоровна
канд. техн. наук, доцент Саратовского государственного технического университета, РФ, г. Саратов
PROBLEM TO STABILITY OF THE FRAME IN THE THEORY OF THE STATIONARY CASUAL PROCESSES
Shlyakhov Stanislav
dr. Sc., Professor, Yuri Gagarin State Technical University of Saratov, Russia, Saratov
Krivulina Elvira
candidate of the technical sciences, Assistant professor, Yuri Gagarin State Technical University of Saratov, Russia, Saratov
АННОТАЦИЯ
Целью работы является получение размеров поперечного сечения рамы, работающей на устойчивость, находящейся под воздействием нагрузки, представляющей стационарный случайный процесс. В работе использован энергетический метод. Получено значение размеров круглого поперечного сечения вероятностным методом. Предлагаемая методика позволяет спроектировать раму при случайном ее нагружении при заданной надежности и сроке эксплуатации.
ABSTRACT
The Purpose of the work is a reception of the sizes of the cross-section of the frame, working at stability, residing under influence of the load, presenting stationary casual process. Energy method is used In the article. It Is Received importance of the sizes of the round cross-section by probabilistic method. Proposed methods allows to design frame under casual its load under given to reliability and period to usages.
Ключевые слова: вероятность; устойчивость; рама
Keywords: probability; stability; frame
Пусть — обобщенная нагрузка, являющая собой случайный нормальный стационарный процесс. В этом случае мерой надежности является вероятность того, что ни разу за срок службы Т действующая нагрузка не превысит критической, т. е. надежность по устойчивости будет равна [1, с. 58]
|
|
(1) |
Решая уравнение (1) при условии ![]() , находим , а через него размеры сечения, обеспечивающие заданную надежность. Для нормального стационарного процесса
, находим , а через него размеры сечения, обеспечивающие заданную надежность. Для нормального стационарного процесса ![]() выражение (1) примет вид
выражение (1) примет вид
|
|
(2) |
Зададим корреляционную функцию в виде
|
|
(3) |
На основании (3) выражение (2) примет вид
|
|
(4) |
Отсюда для имеем
|
|
(5) |
где ![]() .
.
Далее, решая задачу устойчивости, находят ![]() , где — искомый размер сечения, из которого и определяют по значению , взятому по (5).
, где — искомый размер сечения, из которого и определяют по значению , взятому по (5).
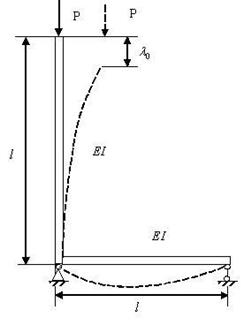
Рисунок 1.
Рассмотрим пример расчета. Рама составлена из двух одинаковых стальных стержней круглого профиля поперечного сечения и нагружена усилием Р (рис. 1).
Нагрузка представляет собой случайный стационарный нормальный процесс. Корреляционная функция имеет вид ![]() .
.
Исходные данные: ![]() м,
м, ![]() кН,
кН, ![]() кН,
кН, ![]() ,
, ![]() ,
, ![]() МПа. Срок службы рамы
МПа. Срок службы рамы ![]() лет
лет ![]() с.
с.
Следует найти размеры поперечного сечения стержней, обеспечивающие надежность по устойчивости ![]() .
.
Решение:
1. Определяем параметр ![]() :
: ![]() .
.
![]() .
.
2. Находим критическую нагрузку : ![]() .
.
![]() кН.
кН.
3. Для связи критического усилия с геометрией рамы решаем задачу устойчивости рамы, предполагая деформации упругими.
Используем энергетический баланс ![]() , где
, где ![]() — работа критической силы,
— работа критической силы, ![]() — потенциальная энергия деформации системы.
— потенциальная энергия деформации системы.
Из энергетического баланса получаем
![]() . (6)
. (6)
Здесь — смещение точки приложения силы вниз.
Для определения потенциальной энергии деформации полагаем форму изогнутой оси подобной от действия поперечной нагрузки ![]() (рис. 2.). Изгибающий момент в произвольном сечении рамы выразится формулой
(рис. 2.). Изгибающий момент в произвольном сечении рамы выразится формулой ![]() .
.
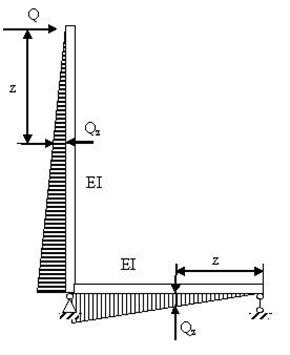
Рисунок 2.
Подсчитаем потенциальную энергию деформации рамы
|
|
(7) |
Осадку (смещение) находим по условию
|
|
(8) |
где ![]() — угол поворота сечения стержня (
— угол поворота сечения стержня (![]() — функция прогиба). Для поиска угла поворота в произвольном сечении
— функция прогиба). Для поиска угла поворота в произвольном сечении ![]() приложим в нем единичный момент и перемножим полученные эпюры
приложим в нем единичный момент и перемножим полученные эпюры ![]() ,
, ![]() по Верещагину (рис. 3):
по Верещагину (рис. 3):
![]()
или для угла поворота
![]() (9)
(9)
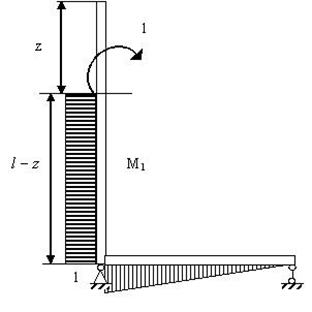
Рисунок 3.
Подставляя (9) в (8) и интегрируя, получаем
|
|
(10) |
На основании (7), (10) из формулы (6) получаем ![]() . Итак:
. Итак:
|
|
(11) |
Определим ![]() из условия (11) для
из условия (11) для
![]() м4
м4 ![]() см4.
см4.
4. Подбираем круглый профиль поперечного сечения из ![]() :
:
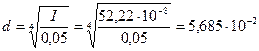 м
м ![]() мм.
мм.
5. Для проверки полученного решения найдем предварительно коэффициент приведения длины ![]() по Эйлеру.
по Эйлеру.
Заменим раму условной стойкой с равным для нее значением критической силы , т. е. ![]() :
: ![]() .
.
Отсюда находим ![]() .
.
6. Проверяем гибкость эквивалентной стойки. Минимальный радиус инерции круглого сечения равен ![]() мм.
мм.
Гибкость стойки ![]() .
.
Получили, что ![]() . Это означает, что найденное решение подчиняется решению Эйлера. Заметим, что в случае гибкости
. Это означает, что найденное решение подчиняется решению Эйлера. Заметим, что в случае гибкости ![]() решение по Эйлеру не справедливо и следует искать решение задачи устойчивости при наличии неупругих деформаций.
решение по Эйлеру не справедливо и следует искать решение задачи устойчивости при наличии неупругих деформаций.
Список литературы:
1.Арасланов А. М. Расчет элементов конструкций заданной надежности при случайных воздействиях. М.: Машиностроение, 1987, — 128 с.
© Э.Ф. Кривулина, 2014.
© С.М. Шляхов, 2014.
дипломов


 ,
, ,
,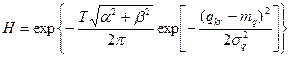 ,
,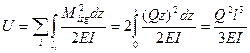 ,
,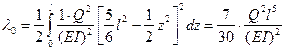 ,
,
Оставить комментарий