Статья опубликована в рамках: XL Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 19 ноября 2014 г.)
Наука: Технические науки
Секция: Материаловедение и металлургическое оборудование и технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
РАСЧЕТ СКОРОСТИ ЧАСТИЦ В ХОЛОДНОМ ГАЗОДИНАМИЧЕСКОМ НАПЫЛЕНИИ
Рябинин Анатолий Николаевич
д-р физ.-мат. наук, гл. научн. сотр. Санкт-Петербургского государственного университета, РФ, г. Санкт-Петербург
E-mail: a _ryabinin@front.ru
PARTICLE VELOCITY CALCULATION IN COLD GAS DYNAMIC SPRAY
Ryabinin Anatoly
D.Sc, Principal Researcher, St. Petersburg State University, Russia, St. Petersburg
Настоящая работа поддержана грантом СПбГУ 6.0.24.2010. Исследования были проведены с использованием вычислительных ресурсов Ресурсного Центра "Вычислительный центр СПбГУ" ( http://cc.spbu.ru).
АННОТАЦИЯ
Проводится сравнение двух методов расчета скорости частиц, разгоняющихся сверхзвуковым потоком газа в процессе холодного газодинамического напыления.
ABSTRACT
A comparison of two methods is performed for calculating the velocity of the particles that are accelerated by supersonic flow in the cold gas dynamic spraying.
Ключевые слова: численный расчет; сопло Лаваля; холодное газодинамическое напыление.
Keywords: numerical calculation; de Laval nozzle; cold gas dynamic spray.
В отличие от других видов термического напыления, в холодном газодинамическом напылении эффективность процесса преимущественно зависит от кинетической энергии напыляемых частиц. Эта кинетическая энергия достигается за счет разгона частиц сверхзвуковым потоком газа [1; 4]. В установках холодного газодинамического напыления используются, как правило, сопла Лаваля с длинной расширяющейся частью круглого или прямоугольного сечения [4]. Для оценки скорости частиц получил распространение приближенный метод, в котором параметры газа в сопле и в струе, исходящей из сопла, рассчитываются на основе одномерной изоэнтропической модели. В этой модели предполагается, что параметры газа зависят только от одной продольной координаты [5; 6; 7]. В настоящей работе результаты расчета скоростей частиц по приближенной модели сравниваются с результатами более полной модели, в которой параметры газа рассчитываются численно с использованием коммерческого пакета ANSYS [2].
Предполагаем, что частицы имеют круглую форму. Уравнения движения частиц вместе с уравнением для температуры, записаны ниже в следующем виде [6]:
|
|
(1) |
|
|
(2) |
|
|
(3) |
где: vp и vg — скорость частиц и газа,
ρp и ρg — плотность частиц и газа,
D — диаметр частиц,
x — координата частицы,
Tp и Tg температура частиц и газа,
k — коэффициент теплопроводности несущего газа,
cp — удельная теплоемкость частиц,
Cx — коэффициент лобового сопротивления частиц, который является функцией чисел Рейнольдса и Маха. Формула для Cx взята из работы [3]. Число Нуссельта Nu, которое является функцией чисел Рейнольдса, Прандтля и Маха вычислялось по формулам из работы [5]. Температура и плотность газа могут быть приближенно вычислены на основе одномерной изэнропической модели. Система обыкновенных уравнений (1), (2) и (3) решается методом Рунге-Кутты.
Однако применение изоэнтропической одномерной модели требует обоснования, поскольку эта модель не учитывает существование пограничного слоя, толщина которого в длинной и узкой расширяющейся части сопла Лаваля может быть сопоставима с поперечным размером сопла. Модель не учитывает также трехмерного характера течения между соплом и напыляемой поверхностью, в частности, не берется во внимание существование скачка уплотнения перед напыляемой поверхностью.
Для учета упомянутых факторов был предпринят численный расчет течения в сопле Лаваля и в пространстве между соплом и напыляемым образцом. Методом конечных объемов решались уравнения Навье-Стокса, осредненные по Рейнольдсу. Принята модель турбулентности k-ω SST. Расчеты проводились с помощью пакета ANSYS CFX [2]. Течение предполагалось осесимметричным. Расчетный объем включал в себя окрестности моделируемого течения. Гибридная расчетная сетка, измельченная вблизи поверхности сопла и напыляемой поверхности, представлена на рис. 1.

Рисунок 1. Расчетная сетка, содержащая 851256 элементов
На входе сопла задавалось постоянное давление, равное 2,5∙106 Па и температура 600 оС. В выходной части расчетного объема среднее давление принималось равным атмосферному давлению. В качестве рабочего газа был выбран воздух. Рассматривалось движение круглых медных частиц. Численный расчет продемонстрировал существование толстого пограничного слоя в сопле и скачка уплотнения перед напыляемой поверхностью. В расчете движения частиц по более полной модели принималось, что частицы движутся вблизи оси симметрии сопла. Частицы вводились в поток в сходящейся части сопла. Их концентрация предполагалась настолько малой, что присутствие частиц не влияло на параметры газового потока.
Результаты расчета скоростей частиц разного диаметра представлены на рис. 2.
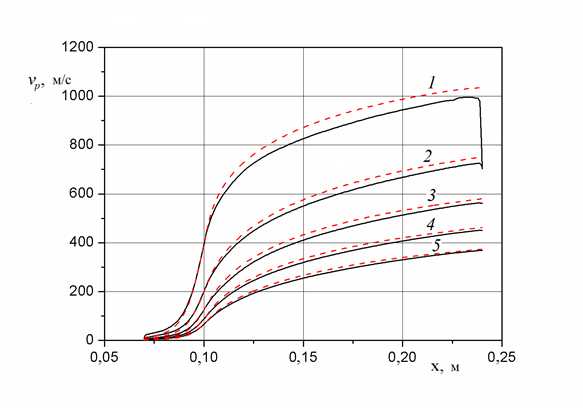
Рисунок 2. Зависимость скорости частиц от продольной координаты. Сплошная линия — вычисления на основе численного расчета течения газа, пунктир — на основе изоэнтропической модели течения в сопле. 1 — D = 1 мкм, 2 — D = 8 мкм, 3 — D = 27 мкм, 4 — D = 64 мкм, 5 — D = 125 мкм
Все кривые на рис. 2, соответствующие одномерной изоэнтропической модели, лежат несколько выше кривых, относящихся к более полной модели. Завышение скорости наиболее велико для малых частиц. Малые частицы подвержены сильному торможению при попадании в зону повышенной плотности после скачка уплотнения перед напыляемой поверхностью. Для крупных частиц диаметром более 8 мкм эффект торможения незначителен. Применение оценочного расчета скорости для крупных частиц дает удовлетворительные результаты.
Список литературы:
1.Алхимов А.П., Клинков С.В., Косарев В.Ф., Фомин В. М. Холодное газодинамическое напыление. Теория и практика. М.: Физматлит. 2010. — 536 с.
2.ANSYS CFX-Solver Modeling Guide. Release 13.0. Canonsburg: ANSYS, Inc. 2010. — 604 p.
3.Henderson C.B., Drag coefficients of spheres in continuum and rarefied flows. AIAA Journal. — 1976. —Vol. 14 (6). — P. 707—708.
4.Irissou E., Legoux J.-G., Moreau C., Ryabinin A.N., Jodoin B. Review on cold spray process and technology: Part I Intellectual property // Journal of Thermal Spray Technology. — 2008. — Vol. 17. — № 4. — P. 495—516.
5.Stoltenhoff T., Kreye H., Richter H.J. An analysis of the cold spray process and its coatings. Journal of Thermal Spray Technology. — 2002. — Vol. 11. — № 4. — P. 542-50.
6.Wong W., Irissou E., Ryabinin A.N., Legoux J.-G., Yue S. Influence of helium and nitrogen gases on the properties of cold gas dynamic sprayed pure titanium coatings // Journal of Thermal Spray Technology — 2011. — Vol. 20. — № 1—2. — P. 213—226.
7.Wong W., Vo P., Irissou E., Ryabinin A.N., Legoux J.-G., Yue S. Effect of Particle Morphology and Size Distribution on Cold-Sprayed Pure Titanium Coatings // Journal of Thermal Spray Technology. — 2013. — Vol. 22. — № 7. — P. 1140—1153.
дипломов


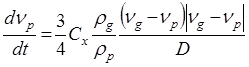 ,
, 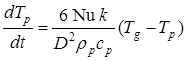 ,
,
Оставить комментарий