Статья опубликована в рамках: XL Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 19 ноября 2014 г.)
Наука: Технические науки
Секция: Инженерная графика, САПР, CAD, CAE
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ГЕОМЕТРИЧЕСКИЕ АСПЕКТЫ В КОНТРОЛЕ ПРОЦЕССА ФУНКЦИОНИРОВАНИЯ ТЕХНИЧЕСКОЙ СИСТЕМЫ
Усенко Валерий Григорьевич
канд. техн. наук, доцент Полтавского национального технического университета имени Юрия Кондратюка, Украина, г. Полтава
E-mail:
Кодак Ольга Антоновна
канд. техн. наук, доцент Полтавского национального технического университета имени Юрия Кондратюка, Украина, г. Полтава
Усенко Ирина Сергеевна
канд. техн. наук, доцент Полтавского национального технического университета имени Юрия Кондратюка, Украина, г. Полтава
THE GEOMETRIC ASPECTS IN MONITORING THE PROCESS OF FUNCTIONING THE TECHNICAL SYSTEM
Valeriy Usenko
candidate of Science, assistant professor of Poltava National Te сhnical Yuri Kondratyuk University, Ukraine, Poltava
Olga Kodak
candidate of Science, assistant professor of Poltava National Te сhnical Yuri Kondratyuk University, Ukraine, Poltava
Irina Usenko
candidate of Science, assistant professor of Poltava National Te сhnical Yuri Kondratyuk University, Ukraine, Poltava
АННОТАЦИЯ
Представлено определение инцидентности точек вектора случайного процесса допустимому двумерному пространству надежности технической системы с позиций геометрии. Граница допустимой области надежности системы для двумерного пространства интерпретируется множеством 0-мерных геометрических объектов (точек) или 1-мерных объектов — линий прямых или кривых, которые соответствуют состоянию системы при определенном наборе параметров. С увеличением размерности допустимого пространства надежности возможные представления границы Г расширяются.
ABSTRACT
It was presented the determining of the preference by the points of the vector of the random process allowable for two-dimensional space of the reliability of the technical system from the geometry position. The boundary of the admissible domain of system reliability for the two-dimensional space is interpreted by the set of 0-dimensional geometric objects (points) or 1-dimensional objects — straight or curved lines, which correspond to the state of the system under a specific set of parameters. With the increase in the allowable space dimension of reliability the possible representations of the boundary Г are expanded.
Ключевые слова: надежность; технические системы; случайные процессы; геометрическое моделирование.
Keywords: reliability; technical systems; casual processes; geometrical design.
Для оценивания надежности технической системы необходимо учитывать характеристики ее поведения во время эксплуатации. Параметры функционирования системы часто имеют случайную природу. Поэтому возникают задачи нахождения вероятностных характеристик поведения системы по заданным вероятностным характеристикам внешних условий воздействия [1; 2; 4].
Надежность Р(t) принимается как вероятность безотказной работы на отрезке времени [0, τ], что соответствует вероятности нахождения вектора v(t) в допустимом пространстве W, ограниченном граничной областью Г в течение этого интервала времени:
|
|
(1) |
В каждый новый момент времени tÎ[0,τ] состояние системы характеризуется конкретным набором параметров пространства надежности p1, p2,..,pm, от числа которых зависит размерность задачи. Элементами пространства надежности может быть надежность элементов системы или надежность подсистем.
Рассмотрим двумерный случай дискретного задания граничной области Г, которое, может быть реализовано путем обработки экспериментальных данных. Точность вычислений зависит от числа точек граничной области ГiÎГ, i=1,2,…,n. Тогда нужно использовать метод интерполяции для получения модели граничной области. Здесь можно применить простейший вариант, когда нужно определить, находится ли точка N{p1,p2} вектора процесса v(t) внутри, снаружи или на некоторой окружности с радиусом, который равен наименьшему расстоянию всех точек дискретной границы Г [3]:
|
|
(2) |
где: p1, p2 — элементы из пространства надежности функционирования системы n — число точек границы Г;
r — расстояние между точкой границы Гi и точкой N{p1,p2} вектора v(t).
Более точным будет определение положения точки N{p1,p2} относительно двух ближайших к ней других точек границы Г. Тогда нужно выполнить интерполяцию ближайшей части границы прямой линией – геометрическим объектом с размерностью 1. Определим ближайшую точку границы к N{p1,p2}:
|
|
(3) |
А также ближайшую точку границы Г к предыдущей:
|
|
(4) |
где: mi, — расстояние от точки границы Гi до точки N{p1,p2},
hi — расстояние от точки границы Гi до ближайшей точки Гi+1.
Положение точки N{p1,p2} относительно прямой (Гі, Гі+1) определяется расстоянием dpl:
|
|
(5) |
Таким образом, условие принадлежности точки N вектора процесса v(t) допустмой области надежности следующее:
|
|
(6) |
Для повышения точности определения положения точки вектора v(t) выполним интерполяцию окружностью, которая проходит через три ближайших точки границы Г к точке N. Интерполяцию части границы выполним в форме кривой, которая проходит через точки Гi-1, Гі, Гі+1. Три точки границы не должны в этом случае принадлежать одной прямой и точка Гі должна быть ближайшей к NÎv(t) соответственно (3). Точки Гi-1 и Гi+1 должны быть ближайшими к Гі соответственно (4). Уравнения прямых (Гi-1, Гі) и (Гі, Гі+1) в неявном виде:
|
|
(7) |
Точка центра окружности ГC находится на равном расстоянии от трех точек границы Гi-1, Гi, Гi+1:
|
|
(8) |
и инцидентна одновременно двум перпендикулярам, проходящим через средние точки отрезков [Гі-1, Гі] и [Гі, Гі+1], которые описываются уравнением:
|
|
(9) |
Параметры центра окружности в двумерном пространстве равны:
|
|
(10) |
Радиус окружности получим как расстояние между точками центра и одной из точек окружности:
|
|
(11) |
Условие принадлежности точки N вектора процесса v(t) допустимой области надежности с частью границы Г, которая аппроксимируется окружностью следующее:
|
|
(12) |
Граница допустимой области надежности системы для двумерного пространства представляется множеством 0-мерных геометрических объектов (точек) или 1-мерных объектов — линий прямых или кривых. Переход от объектов меньшей размерности границы к объектам большей размерности осуществляется методом интерполяции. С увеличением размерности допустимого пространства надежности системы возможные представления границы Г расширяются. Например, в трехмерном пространстве необходимо рассматривать также двумерные объекты: плоскости и поверхности.
Список литературы:
1.Болотин В.В. Методы теории вероятностей и теории надежности в расчетах сооружений. М.: Стройиздат‚ 1981. — 351 с.
2.Капур К, Ламберсон Л. Надежность и проектирование систем. М.: Мир‚ 1978. — 432 с.
3.Корн Г.‚ Корн Т. Справочник по математике. М.: Наука‚ 1974. — 832 с.
4.Пичугин С.Ф. Надежность стальных конструкций производственных зданий: Монография. Полтава: Издательство «АСМІ», 2009. — 451 с.
дипломов



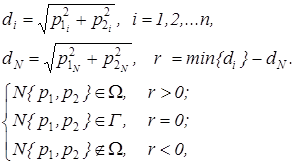


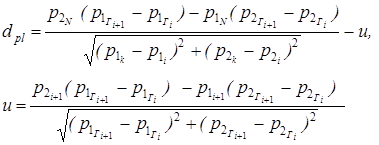
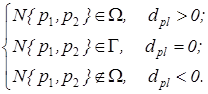

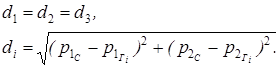
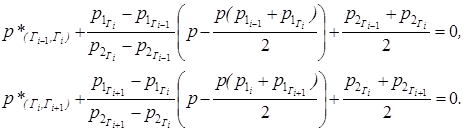
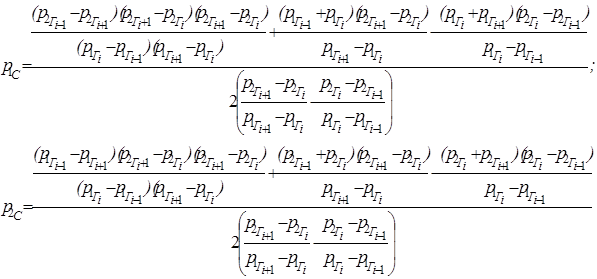
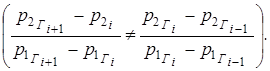
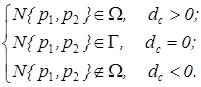
Оставить комментарий