СЖАТИЕ  АНИЗОТРОПНОГО  ИДЕАЛЬНОПЛАСТИЧЕСКОГО  СЛОЯ  ПРИ  ОБОБЩЕНИИ  УСЛОВИЯ  ПЛАСТИЧНОСТИ  МИЗЕСА-ХИЛЛА

Балашникова  Анжелика  Вениаминовна

аспирант  кафедры  математического  анализа  Чувашский  государственный  педагогический  университет  им.  И.Я.  Яковлева,  г.  Чебоксары

E-mail: 

COMPRESSION  OF  ANISOTROPIC  IDEALLY  PLASTIC  LAYER  AT  GENERALIZATION  OF  THE  CONDITION  OF  PLASTICITY  OF  MIZESA-HILLA

Balashnikova  Anshelika

Postgraduate  student,  Departament  of  Mathematical  Analysis,  I.  Yakovlev  Chuvash  State  Pedagogical  University,  Cheboksary

АННОТАЦИЯ

В  работе  рассматривается  предельное  состояние  слоя  из  идеальнопластического  материала  при  трансляционной  анизотропии,  сжатого  параллельными  шероховатыми  плитами  [2].

ABSTRACT

In  work  the  limit  condition  of  a  layer  from  an  idealnoplastichesky  material  is  considered  at  the  transmitting  anisotropy,  squeezed  by  parallel  rough  plates.

Ключевые  слова:  сжатие;  слой;  идеальная  пластичность;  трансляционная  анизотропия.

Keywords:  compression;  layer;  ideal  plasticity;  transmitting  anisotropy

Запишем  уравнения  равновесия 

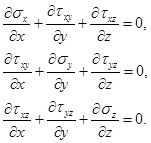   (1)

Условие  пластичности  [1]  запишем  в  виде

  (2)

где:    —  компоненты  напряжения,  ,  определяющие  предел  текучести  и  параметры  анизотропии.

В  дальнейшем  перейдем  к  безразмерным  величинам,  все  величины,  имеющие  размерность  напряжений  отнесем  к  величине  предела  текучести    и  сохраним  обозначения  напряжений  .

Условие  пластичности  (2)  примет  вид

  (3)

Соотношения  связи  между  напряжениями  и  скоростями  деформаций  согласно  ассоциированному  закону  течения,  имеют  вид

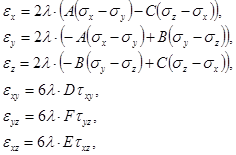   (4)

где:    —  компоненты  скорости  деформации.

Из  (4)  следует  условие  несжимаемости

   (5)

Используя  условие  несжимаемости  (5)  из  (4)  выразим:

   (6)

Подставляя  полученное  выражение  (6)  в  ассоциированный  закон  течения  (4)  найдем

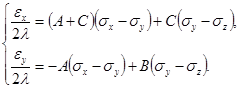   (7)

Определитель  данной  системы  (7)  равен

Найдем  решения  системы  (7):

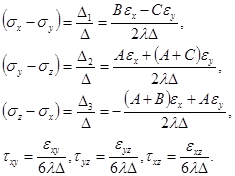   (8)

Полученное  решение  подставим  в  уравнение  пластичности  (2)  и  выразим  :

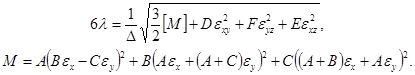  (9)

Имеют  место  формулы  Коши

 ,  ,  ,  ,  ,    (10)

где:  ,  ,    —  скорости  перемещения.

Имеем 

 .  (11)

Используя  (11)  из  (4)  выразим  напряжения  через  компоненты  скорости  деформации:

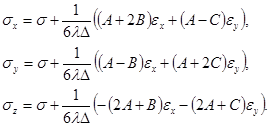   (12)

Предположим,  что  все  компоненты  девиаторов  напряжений,  и  скорости  деформации  ,  зависят  только  от  :

   (13)

Положим  аналогично  Прандтлю:

   (14)

где: 

Из  (4),  (14)  следует

   (15)

Согласно  принятым  предположениям  уравнения  равновесия  (1)  примут  вид

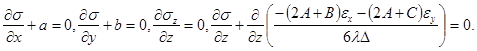   (16) 

Из  (16)  находим

   (17)

Условие  несжимаемости  (5),  согласно  (10),  имеет  вид

   (18)

Положим

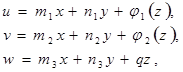   (19)

где: 

Согласно  (10),  (18)  формулы  Коши  перепишем,  учитывая  предположение  (14)  получим

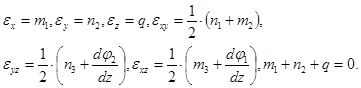        (20) 

Для  нахождения    в  соотношение  (9)  подставим  полученные  формулы  Коши  (20)  и  найдем:

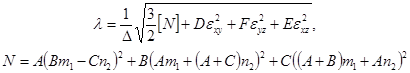   (21)

Согласно  (12),  (15),  (17),  (20)  получим

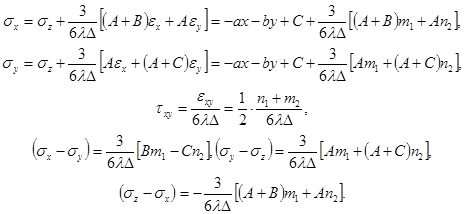   (22)

В  условие  пластичности  (3)  подставим  предположение  (14),  полученные  формулы  для  напряжений  (22)  и  найдем  : 

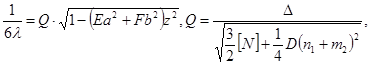
  (23)

Обозначим  толщину  слоя  ,  предположим,  что  в  некоторой  точке    определено  осредненное  давление

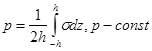   (24)

Для  нахождения  константы    подставим  полученные  данные  (16),  (23),  в  формулу  (24),  сделав  преобразования,  получим: 

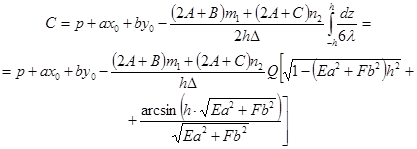   (25)

Согласно  (17),  (23),  (25)  величина  сдавливающего  напряжения    будет  зависеть  от  характера  деформирования  плиты.

Список  литературы:

1.Балашникова  А.В.  О  сжатии  пространственного  идеальнопластического  слоя  при  трансляционной  анизотропии  при  обобщении  условия  пластичности  Мизеса  //  Вестник  Чуваш.  гос.  пед.  ун-та  им.  И.Я.  Яковлева.  Серия:  Механика  предельного  состояния.  —  2012.  –  №  1  (11).  —  С.  56—59.

2.Максимова  Л.А.  О  предельном  состоянии  слоя,  сжатого  шероховатыми  плитами  //  ПММ.  —  2000.  —  Т.  64.  Вып.  6.  —  С.  1099—1104.