Моделирование распространения сигнала в среде движущихся объектов с применением функций Уолша

Прокошев Валерий Валерьевич

аспирант ВлГУ, г. Владимир

E-mail: valery.prokoshev@gmail.com

Скляренко Василий Алексеевич

канд. физ.-мат. наук, доцент, профессор ВлГУ, г. Владимир

E-mail: skv@vlsu.ru

Шамин Павел Юрьевич

канд. техн. наук, доцент ВлГУ, г. Владимир

E-mail: trace83@mail.ru

Modelling a signal diffusion in mobile environment using Walsh functions

Valery Prokoshev

Graduate student of VlSU, Vladimir

Vasily Sklarenko

Candidate of Physical and Mathematical Sciences, Associate Professor, Professor of VlSU, Vladimir

Pavel Shamin

Candidate of Technical Sciences, Associate Professor of VlSU, Vladimir

Аннотация

В статье исследуется процесс распространения сигнала в неорганизованной среде подвижных объектов. Предложена модель на основе функций Уолша. Приведены результаты компьютерного моделирования.

Abstract

In this clause, a process of signal distribution in the unorganized environment of mobile objects are considered. The model based on the Walsh functions are offered. Some results of computer modelling are presented.

Ключевые слова: мобильная сеть; функции Уолша; моделирование.

Keywords: mobile network,;Walsh functions; modelling.

Данная работа выполнена в рамках НИР по госзаданию «Наука» (Регистрационный номер: 8.3534.2011 от 23.11.2011).

Описание модели

Рассмотрим распространение сигнала в неорганизованной среде, состоящей из движущихся объектов (например, такой, как в работах [3] и [4]).

Положим в основу такую характеристику сети как «концентрация активных связей» — процент активных связей по отношению к их общему количеству в сети в данный момент времени. Работающая динамическая сеть это набор доменов (домен — множество объектов сети). Каждый домен имеет различную концентрацию активных связей, меняющуюся со временем. Пусть 0<C[t]<1 концентрация всей сети; исследуется отрезок времени . Из теории перколяции следует, что  такое, что при ,  сигнал проходит через сеть почти наверное ( — порог перколяции). Пусть . Тогда мы можем получить приближение  при помощи разложения по базису Уолша (о функциях Уолша см. [1] и [2]):

, где v_i — функция Уолша, i=0,...,I.

Рассмотрим следующую модель. Узлы сети расположены в узлах квадратной решетки NxM, и L — количество связей. Наличие связи в каждый момент определяется по функциям Уолша. Введем обозначения: v_i — функция Уолша (причём v₀ — константа равная 1). Пусть значение 1, в определенный момент времени, соответствует активности связи, а (–1) — неактивности. Пусть время принимает дискретные значения , i=0,...,I.

Инструментом моделирования является построение синхронизированных доменов cl_i, i=0...I. Домен cl_i — это подмножество связей, работающих синхронно. Связи в домен выбираются случайно, так что:

| cl_i| = 2n_i

Пусть , тогда предполагается, что n_i связей работают в режиме v_i, а оставшиеся связи домена работают в инверсионном режиме, то есть . Таким образом, в каждый момент времени активными являются ровно n_i (50 %) связей ненулевого домена. Назначение режимов внутри домена также производится случайно. Режимы функционирования связей внутри домена синхронизированы. Разные домены переключаются независимо, поскольку соответствующие им функции Уолша ортогональны. Количество связей в домене cl₀ задается входным параметром. Также входным параметром является относительное количество узлов домена cl₀ работающих в прямом режиме. Размер остальных доменов подбирается так, что они имеют равный объем и охватывают всю сеть.

Функционирование сети, построенной, как указано выше, обеспечивает постоянство глобального параметра сети — процент активных связей в произвольный момент времени. Таким образом продвижение сигнала с ожиданием происходит за счет локальных перестроек. Процесс передачи обрывается когда время моделирования превысит I или сигнал достигнет конечного узла. Обозначим t_n среднее время, за которое был достигнут слой n и последовательности, а k_n — количество испытаний из общего числа испытаний R, в которых сигнал побывал на n-м слое, где  и последовательности относительных частот .

Исследуем зависимость времени прохождения сигнала от количества слоев между слоем источником и слоем приемником, а также вероятность прохождения сигнала через систему.

Численный эксперимент

Эксперимент проводился на разработанном нами параллельном сетевом симуляторе, установленном на суперкомпьютерной системе [5]. Моделировалась квадратная решетка размером . Размер домена cl₀ — 40 % от всех связей, количество доменов I=8. Рассмотрены два случая: количество прямых связей в нулевом домене 20 % и 25 % от количества связей в cl₀. Количество запусков эксперимента для сбора статистики — 1000 запусков.

В результате эксперимента были получены зависимости достигнутого слоя от времени (рис. 1) и вероятности прохождения сигнала через систему (рис. 2).

Рисунок 1. Время t_n, за которое достигнут слой n

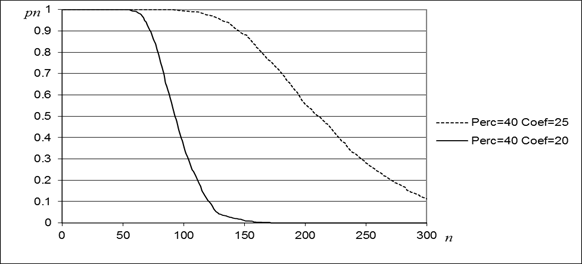
Рисунок. 2. Вероятность pn с которой достигнут слой n

Также были получены гистограммы распространения фронта волны для каждого момента времени. На них показано количество запусков k_n, для которых сигнал в момент времени t остановился на слое n (см. рис. 3).

Из полученных результатов можно сделать вывод, что вероятность прохождения сигнала резко увеличивается при сравнительно небольшом увеличении связей, которые постоянно активны. Прохождение сигнала через систему наблюдается даже в случаях, когда порог перколяции для квадратной решетки не достигнут.

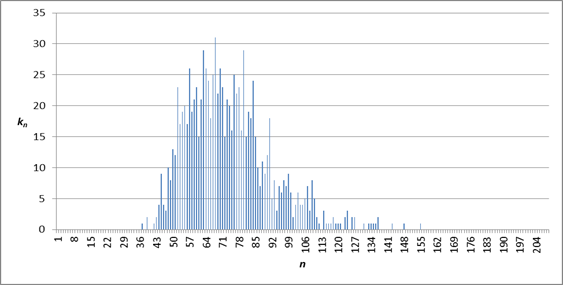
Рисунок 3. Гистограмма распространения фронта волны при t=5.

Список литературы:

1.Голубов, Б.И. Ряды и преобразования Уолша: Теория и применения. / Голубов Б.И., Ефимов А.В., Скворцов В.А. // М.: Наука. гл. ред. физ.-мат. лит., 1987. — 344 с.

2.Малозёмов, В.Н. Дискретные функции Уолша // Семинар «DHA&CAGD». Избранные доклады. 12 марта 2011 г. (http://dha.spb.ru/PDF/WalshFunctions.pdf).

3.Прокошев В.В., Аракелян С.М., Скляренко В.А. Некоторые особенности распространения сигнала в среде движущихся объектов // Труды XVIII Всероссийской научно-методической конференции «Телематика’2011». — 2011. — Т. 2. — С. 300—301

4.Прокошев В.В., Скляренко В.А. О прохождении сигнала по цепи движущихся объектов // Труды XVII Всероссийской научно-методической конференции «Телематика’2010». — 2010. — Т. 2. — С. 251—253

5.Шамин П.Ю., Алексанян А.С., Прокошев В.В. Параллельный сетевой симулятор: концепция и перспективы развития // Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. — СПб. 2009. — № 3. — С. 18—24.