КРИТЕРИИ ПРИНЯТИЯ В АЛГОРИТМЕ СИМУЛЯЦИИ ОТЖИГА

Карпов Пётр Михайлович

аспирант Вычислительного центра им. А.А. Дородницына Российской академии наук, г. Москва

E-mail: Reoser@mail.ru

ACCEPTANCE CRITERIA IN THE SIMULATED ANNEALING ALGORITHM

Peter Karpov

Postgraduate, Dorodnicyn Computing Centre, Moscow

Аннотация

Целью работы является изучение различных критериев принятия в алгоритме симуляции отжига. Рассматриваются существующие (Метрополиса, Цаллиса, Баркера, пороговое принятие) и оригинальные критерии. Эффективность критериев сравнивается на различных проблемах оптимизации: синтетическая тестовая функция, задача коммивояжёра, минимальное линейное размещение, построение магических квадратов, раскраска графа.

Abstract

Present work studies different acceptance criteria in the simulated annealing algorithm. Existing (Metropolis, Tsallis, Barker, threshold acceptance) and original criteria are examined. Their efficiency is compared using different optimization problems: synthetic test function, traveling salesman problem, minimal linear arrangement, magic squares construction, graph coloring.

Ключевые слова: симуляция отжига; комбинаторная оптимизация

Keywords: simulated annealing; combinatorial optimization

Введение

Симуляция отжига (СО) — алгоритм оптимизации, предложенный Киркпатриком [5] и независимо Черны [1], являющийся адаптацией алгоритма выборки Метрополиса [6]. СО имитирует процесс отжига в металлургии, при котором металл нагревается до температуры выше температуры кристаллизации и затем медленно охлаждается. Этот процесс устраняет внутреннее напряжение и в результате приводит к кристаллической решётке с малой внутренней энергией. СО находит широкое применение благодаря эффективности и простоте реализации.

Сформулируем проблему оптимизации: найти решение x, максимизирующее или минимизирующее целевую функцию (ЦФ) E(x). Допустим также, что имеется метод генерации случайных ходов, переводящих решение x в соседнее решение x’. На каждом шаге рассмотрению подвергается новое соседнее решение. В отличие от стохастического восхождения (hillclimbing), которое принимает лишь ходы, приводящие к улучшению, СО иногда принимает ходы, ухудшающие значение ЦФ, что позволяет ей выходить из локальных оптимумов. Без ограничения общности допустим, что мы имеем дело с проблемой минимизации. В классическом СО используется критерий Метрополиса: вероятность принятия хода, приводящего к изменению энергии (ЦФ)  есть

,

где  — параметр по аналогии с оригинальным процессом называемый температурой и имеющий ту же размерность, что и ЦФ. Все ходы, приводящие к улучшению () принимаются, но вероятность принятия ухудшающих ходов () зависит от температуры. Лишь ходы с  порядка T имеют значительный шанс принятия, в то время как ходы с  скорее всего будут отвергнуты. Изменяя параметр , можно контролировать свойства поиска: при очень высоких температурах принимаются почти все ходы (случайный поиск, жидкое состояние), в то время как при очень низких температурах принимаются лишь хорошие ходы (локальный поиск, кристаллическое состояние). СО работает, постепенно понижая температуру, что позволяет изучить пространство поиска сначала на грубом, а затем на более тонком уровне. Более детальное рассмотрение аналогий между оптимизацией и статистической механикой может быть найдено в оригинальной статье [5].

Обобщённая процедура СО может быть записана следующим образом:

i := 0                          Сбросить счётчик итераций

x := Random_Solution                  Создать начальное решение

Best := x

repeat

x' := Random_Neighbour(x)      Сгенерировать соседнее решение

dE := E(x') – E(x)             Вычислить изменение энергии

T := Schedule(i)                     Выбрать температуру

if Random < P(dE / T) then           Принять или отвергнуть

      x := x'                   пользуясь критерием принятия

if E(x) < E(Best) then         Обновить лучшее решение

      Best := x

i := i + 1

until Stopping_Condition              Проверить критерий остановки

return Best                     Вернуть лучшее решение

Таким образом, для реализации СО необходимы следующие элементы:

·     Формулировка задачи

◦  Пространство решений

◦  Целевая функция

◦  Функция генерации случайного соседа

·     Параметры алгоритма

◦  Температурный режим

◦  Функция принятия ,

◦  Критерий остановки

Температурным режимам и различным модификациям базового алгоритма посвящено значительное количество работ, однако функции принятия уделяется меньше внимания. Данная работа является попыткой предпринять исследование, направленное на изучение её влияния.

Начальная и конечная температуры

Критерием остановки в данной работе является достижение фиксированного количества итераций . В качестве температурного режима используется геометрическое охлаждение:

, ,

где  и  — начальная и конечная температуры соответственно. Оно является самым популярным режимом, так как обеспечивает быстрое охлаждение (и соответственно скорость сходимости) и демонстрирует хорошие результаты на практике. Для исследования работы алгоритма на различных задачах необходим универсальный способ выбора параметров  и .

Изначально система должна находиться в жидком состоянии, когда принимаются почти все ходы. В противном случае температурных флуктуаций энергии может быть недостаточно для преодоления высоких потенциальных барьеров и решение застрянет в области, далёкой от оптимума. Возможный способ оценки  — произвести начальный поиск при бесконечной температуре (принимая все ходы). Начальная температура должна иметь тот же масштаб, что и изменения энергии соседних решений  во время этой стадии. В данной работе используется выражение, основанное на средне модуле изменения энергии:

,

В конце поиска температура должна быть достаточно мала, чтобы почти все ухудшающие ходы отвергались, иначе решение не достигнет локального оптимума. Если минимально значимое изменение ЦФ обозначить , то вероятность принятия хода, приводящего к такому изменению в конце поиска , а среднее число итераций до принятия . В условной «холодной фазе» (последние  итераций) ни одно минимальное ухудшение не должно быть принято:

,

Эта оценка является завышенной, так как основана на минимальной температуре, в то время как в начале холодной фазы температура и, следовательно, вероятность принятия ухудшающих ходов может быть значительно выше. Поэтому воспользуемся несколько меньшим значением:

, ,

И хотя приведённые рассуждения основываются на грубых прикидках, для большинства задач они дают вполне адекватные оценки параметров  и .

Функция принятия

Стандартная функция принятия, унаследованная от алгоритма Метрополиса

,

но в принципе ничто не мешает использовать какую-либо другую. Популярный альтернативный критерий — пороговое принятие (threshold accepting), являющееся детерминированным:

В отличии от критерия Метрополиса, критерий Баркера может иногда отвергать ухудшающие ходы:

Ещё один критерий основан на обобщённой формулировке статистической механики Цаллиса [9]:

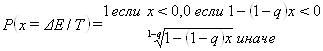
В работе [8] показано, что многие критерии принятия эквивалентны критериям Метрополиса или Баркера после монотонного преобразования температуры. Тем не менее, на практике может быть более удобно работать с фиксированным семейством температурных режимов, но менять функцию принятия — подход, принятый в данной работе. Различные семейства обобщённых функций принятия приведены в таблице 1:

Таблица 1

Семейства критериев принятия

Наиболее важным параметром функции принятия является её асимптотическое поведение при . Медленно затухающие, тяжёлые «хвосты» дают высокую вероятность принятия больших ухудшающих изменений. С одной стороны это даёт возможность перепрыгнуть высокие потенциальные барьеры и выбраться из локального минимума. С другой стороны, это может привести к недостаточному изучению около-оптимального региона. Чем тяжелее хвост, тем менее локален поиск.

Результаты тестирования

Для выяснений особенностей функций принятия были использованы различные тестовые задачи:

·     Тестовая функция (ТестФ)

◦  Формулировка:

Мультимодальная тестовая функция, схожая с функцией Растригина [11].

◦  Энергия:

,

◦  Случайный ход:

, ,  - случайное число со стандартным нормальным распределением.

·     Задача коммивояжёра (ЗКВ) [7]

◦  Формулировка:

Обойти заданные точки замкнутым маршрутом, имеющим минимальную длину.

◦  Энергия:

Суммарная длина маршрута.

◦  Случайный ход:

2-Opt: разорвать маршрут в двух случайных местах и пересоединить два получившихся пути [7].

·     Магический квадрат (МагКв)

◦  Формулировка:

Заполнить массив  числами от 1 до  так, чтобы сумма чисел во всех строках, столбцах и диагоналях была одинакова.

◦  Энергия:

Сумма абсолютных отклонений сумм в строках, столбцах и диагоналях от магической константы .

◦  Случайный ход:

Обменять значения в двух случайно выбранных ячейках.

· Минимальное линейное размещение (МинЛР) [3]

◦  Формулировка:

Заполнить массив  числами от 1 до  так, чтобы минимизировать сумму абсолютной разницы между числами во всех соседних ячейках.

◦  Энергия:

◦  Случайный ход:

Обменять значения в двух случайно выбранных ячейках.

·     Раскраска графа (РГ) [2]

◦  Формулировка:

Раскрасить вершины графа фиксированным количеством цветов так, чтобы никакие две соседние вершины не имели одинаковый цвет.

◦  Энергия:

Количество соседних вершин, имеющих одинаковый цвет.

◦  Случайный ход:

Присвоить случайный цвет случайной вершине.

Таблица 2

Параметры тестовых задач

Начальные и конечные температуры выбирались автоматически в соответствии с ранее описанными методами. Исключением является критерий Баркера, ввиду обратной функции принятия которого вместо  использовался множитель . Для уменьшения влияния метода выбора конечной температуры на результаты, тесты проводились для двух значений параметра m, 0.5 и 1. Максимальное количество итераций подбиралось так, чтобы вероятность нахождения глобального оптимума была достаточно значительной (обычно около 10 % или выше). Для каждой проблемы было выполнено 10'000 независимых запусков алгоритма. В качестве меры успеха того или иного критерия принятия служило среднее отклонение энергии полученного решения от энергии глобального оптимума:

Для тестовой функции ввиду на порядки отличающихся результатов отдельных запусков использовалось среднее геометрическое.

Во всех случаях критерий Баркера дал худшие результаты, чем критерий Метрополиса, проиграв по отклонению от оптимума в среднем в 1.3 раза. Поведение остальных критериев продемонстрировало зависимость от проблемы. Тестовая функция и ЗКВ отдают явное предпочтение пороговому принятию. Для других проблем поведение критериев принятия более интересно: для каждого семейства обычно существует оптимальное конечное значение параметра, а семейством, дающим наилучший результат обычно оказывается степенное (см. таблицу 3).

Таблица 3

Оптимальные критерии принятия в виде (семейство, параметр). Обозначения: ПП — пороговое принятие, ст — степенной, е — экспоненциальный.

Таблица 4

Лучшие параметры в рамках семейств критериев принятия

Насколько велик проигрыш при использовании различных критериев принятия в сравнении с оптимальными? Для выяснения этого вопроса средние отклонения от оптимума для каждой проблемы и параметра m были нормализованы по отношению к наилучшему значению. Обработанные таким образом результаты тестов приведены в таблице 5. Пороговое принятие считается членом каждого семейства ввиду соответствующих пределов.

Таблица 5

Нормализованные средние отклонения для порогового принятия, критерия Метрополиса и оптимальных критериев из различных семейств

Заключение

В настоящей работе были рассмотрены различные критерии принятия в алгоритме симуляции отжига: Метрополиса, Цаллиса, Баркера, пороговое принятие, экспоненциальное и степенное семейства. Наиболее важным свойством критерия принятия P(y) является его асимптотическое поведение при . Функции с тяжёлыми хвостами имеют больший шанс вывести застрявшее решение из потенциальной ямы, но в то же время уменьшают интенсивность исследования небольших областей пространства поиска.

Критерии подверглись сравнению на пяти различных задачах: синтетическая тестовая функция, задача коммивояжёра, построение магических квадратов, минимальное линейное размещение, раскраска графа. Поведение критериев оказалось сильно зависимым от проблемы. В двух задачах (тестовая функция, задача коммивояжёра) наилучшие результаты дало пороговое принятие, в большинстве остальных случаев — функция из степенного семейства с конечным параметром. При правильном выборе параметра функции принятия, все три семейства (экспоненциальное, степенное, Цаллиса) демонстрируют результаты, очень близкие к лучшим.

Наиболее популярный критерий Метрополиса занимает промежуточное положение между пороговым принятием и функциями с тяжёлыми хвостами. Обычно он даёт несколько субоптимальные результаты, но тем не менее в половине тестов выигрывает у порогового принятия. Критерий Баркера во всех случаях уступает критерию Метрополиса. Применение подобных критериев, отвергающих часть улучшающих ходов, в контексте симуляции отжига следует считать нецелесообразным.

Перебор различных функций принятия может улучшить качество получаемых решений, но в то же время является весьма трудоёмкой процедурой. На основе анализа результатов проведённых вычислительных экспериментов можно предложить простое правило. Выбор следует делать из трёх критериев: порогового принятия, критерия Метрополиса и функции с тяжёлым хвостом (степенное семейство,  или критерий Цаллиса, ).

Список литературы:

1.Černý, V. "Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm". Journal of Optimization Theory and Applications 45: 41—51.

2.Duffany J.L. “Complexity Analysis of Some Known Graph Coloring Instances”. World Academy of Science, Engineering and Technology 63, 2010.

3.Fishburn P., Tetali P., Winkler P. “Optimal linear arrangement of a rectangular grid”. Discrete Mathematics, 2000: 123—139

4.Graph Coloring Instances. http://mat.gsia.cmu.edu/COLOR/instances.html

5.Kirkpatrick, S., Gerlatt C.D., Jr., Vecchi M.P. “Optimization by Simulated Annealing”, Science 220, 671—680.

6.Metropolis N., Rosenbluth A.W., Rosenbluth M.N., Teller A.H., Teller E. "Equation of State Calculations by Fast Computing Machines". The Journal of Chemical Physics 21 (6): 1087.

7.Nilsson C. “Heuristics for the Traveling Salesman Problem”. Tech. Report, Linköping University, Sweden, 2003. www.ida.liu.se/~TDDB19/reports_2003/htsp.pdf

8.Schuur P.C. “Classification of acceptance criteria for the simulated annealing algorithm”. Mathematics of Operations Research Vol. 22, No. 2, May, 1997

9.Tsallis C., Stariolo D.A. “Generalized simulated annealing”. Physica A 233, Issue: 1—2, P. 395—406, 1995

10.TSPLIB http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/

11.Yang X.-S. “Test problems in optimization”. Engineering Optimization: An Introduction with Metaheuristic Applications (Eds Xin-She Yang), John Wiley & Sons, 2010