Статья опубликована в рамках: XI Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 25 июня 2012 г.)
Наука: Технические науки
Секция: Машиностроение и машиноведение
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Постановка задачи экспериментальных исследований колебаний винтовых цилиндрических пружин
Полищук Андрей Дмитриевич
канд. техн. наук, доцент ИжГТУ, г. Ижевск
Е-mail: apolischuk@mail.ru
Гаранкина ЕленаНиколаевна
магистрант, ИжГТУ, г. Ижевск
Е-mail: lamial69@gmail.ru
FORMULATION OF THE HELICAL SPRINGS EXPERIMENTAL INVESTIGATION PROBLEM
Andrey Polischuk
Cand. Technical , Associate Professor of Izhevsk Technical State University, Izhevsk
Elena Garankina
undergraduate of Izhevsk Technical State University, Izhevsk
АННОТАЦИЯ
Обсуждаются физика взаимосвязанных пространственных колебаний винтовых цилиндрических пружин и имеющиеся экспериментальные результаты. Ставиться задача по исследованию колебаний пружине с целью исследования физики взаимосвязанных колебаний винтовых цилиндрических пружин.
ABSTRACT
The physics and experimental data spatial interconnected oscillation of cylindrical helical springs are discussed. The experimental research problem of helical spring oscillation is formulated with the goal of helical springs oscillation physics investigations.
Ключевые слова: винтовые пружины; колебания; взаимосвязанность; нелинейность.
Keywords: helical springs; oscillation; interconnected; nonlinearity.
Винтовые цилиндрические пружины и пружинные механизмы играют важную роль в современной технике. Для многих пружин динамические явления: колебания, устойчивость и удар чрезвычайно важны. Важнейшим компонентом для исследования динамических явлений в пружинах и пружинных механизмах является исследование колебаний пружин: собственных частот и форм, вынужденных колебаний.
Кроме того, что понимание динамических явлений в пружинах важно для повышения долговечности и качества работы пружинных механизмов, это важно и как модельная задача. Пружины имеют сложный частотный спектр, частотный спектр несамосопряженной задачи – это интересно теоретически. В пружинах, при определенных допущениях, имеется аналитическое решение для теории колебаний. Это возможно, т. к. пружины, обладая геометрической нелинейностью, физически линейны. Пружины, как упругий элемент, работают при напряжениях, как правило, существенно меньше пределов пропорциональности. Соответственно, перемещение и вращение в пружина, жестко связаны друг с другом. Понимание физики взаимосвязанных пространственных колебаний винтовых цилиндрических пружин может помочь в понимании процессов, в которых имеется одновременно перемещение и вращение, но в которых аналитическое решение невозможно. Пружины – своеобразная «муха-дрозофила» механики.
Чтобы вести разговор о постановке задач экспериментальных исследований, кратко опишем методику решения теории колебаний винтового тонкого бруса в Ижевской школе. Используются классические уравнения Кирхгоффа-Клебша для винтового тонкого бруса [3] (уравнения Бернулли-Эйлера). Рассматриваются малые колебания относительно больших предварительных деформаций: поджатие и закрутка. Система координат естественная: нормаль, бинормаль и тангенциальная координата.
Реализовано два варианта граничных условий: жесткая заделка с обычными для жесткой заделки граничными условиями и своеобразное шарнирное опирание.
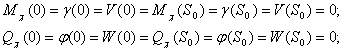
При шарнирном опирании и ряде допущений, получаем частотное биквадратное уравнение, его называем «порождающим решением», график на рисунке 1.
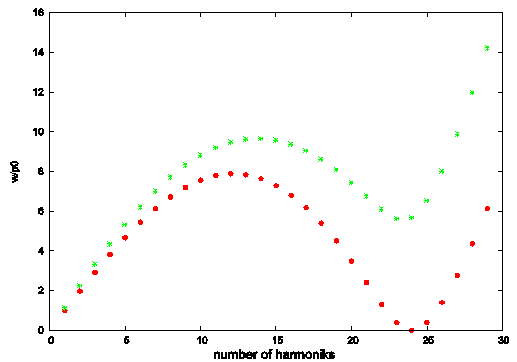
Рис.1 Частотный спектр при «порождающем решении» для i=12 (количество рабочих витков), ![]() a=60 (угол подъёма винтовой линии), m=0 (относительное поджатие)
a=60 (угол подъёма винтовой линии), m=0 (относительное поджатие)
При жесткой заделке расчет частот ведется численным методом по аналитической зависимости: искомая собственная частота обращает в верное тождество характеристическое уравнение и граничное уравнение. Построены формы колебаний по шести координатам.
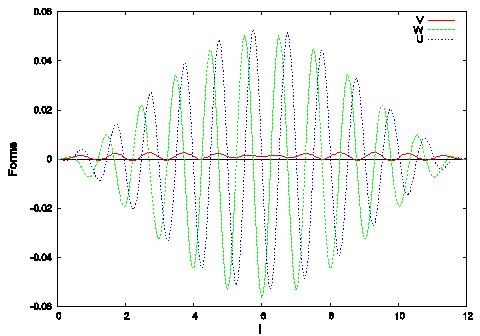
Рис. 2 Формы колебаний вдоль винтовой линии пружины для i=12, m=0,1, a=60, w/p0=0,79 (безразмерная частота), антисимметричная мода. Координаты: U – нормаль, V – бинормаль. W - тангенциальная
Особенность колебаний винтовых цилиндрических пружин — форма колебаний каждой моды имеет все шесть пространственных компонент, находящихся в определенной связи (рисунок 2). Исходя из этого, можно говорить о взаимосвязанных колебаниях пружины. Для пружин нет чисто продольных или чисто поперечных колебаний, тем не менее, в технической литературе по пружинам, обычно используется терминология эквивалентного бруса: продольные, поперечные, крутильные колебания. В данном случае продольные и поперечные колебания рассматриваются относительно оси пружины. Двум ветвям характеристического уравнения соответствуют две волны, существующие в твердом теле (рисунки 2, 3).
Следующая особенность частотного спектра винтовых цилиндрических пружин – возможность близкого совпадения основных частот пространственных продольных, поперечных и крутильных колебаний, также и других. При близком совпадении наблюдается взаимная модуляция форм колебаний, например, при близком совпадении пространственных продольных и поперечных колебаний в поперечных гармониках наблюдаются продольные компоненты, а в пространственной продольной – поперечные. Более подробно по физике пространственных колебаний винтовых пружин [2, 7].
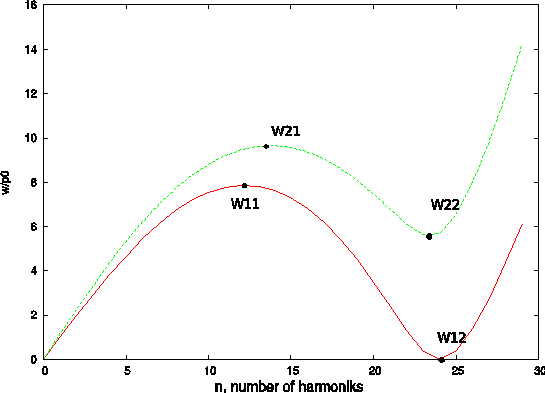
Рис. 3 «Особые» частоты (нераспространяющиеся моды) и их место на характеристическом уравнении
Экспериментальных исследований частотного спектра было, как ни странно, совсем немного.
В первую очередь стоит упомянуть эксперименты грузинской школы: Хвингия М.В., Мгалоблейшвили Д.Б. [4]. Выполнен достаточно большой объем исследований. Основные недостатки: невысокая точность вследствие выбранной методики исследования и параметров пружины и при проведении экспериментов на исследователей давила «модель» эквивалентного бруса. Хвингия М.В. считал, что все виды колебаний объясняются эквивалентным брусом и кратными частотами, отдельно рассматривались продольные, крутильные и поперечные колебания. Считалось, что если возбуждаются продольные колебания, то будут реализованы только продольные. Однако, как показано в [2], за кратную к продольной частоте частоту принята одна из крутильных, поскольку в пружинах они возбуждаются одновременно.
Эксперименты ижевской школы [1, 2], на наш взгляд, наиболее точные и объемные, однако при проведении эксперимента была нехватка времени и эксперимент проводился, во многом, с целью подтверждения теоретических расчетов.
Зарубежных экспериментов авторам известно три, ссылки имеются на две [5, 6]. Обычно, испытывались одна-две пружины, в самых простых для расчетов случаях. Эти результаты кочуют из статьи в статью тех, кто занимается расчетами. По результатам видно, что эксперимент проводился с целью подтверждения теоретических расчетов.
Итак, об экспериментальных исследованиях винтовых цилиндрических пружин можно сказать следующее: их очень немного, они проводились, главным образом, с целью подтверждения теоретических результатов.
Исходя из вышеизложенного, можно сформулировать задачу экспериментальных исследований колебаний винтовых цилиндрических пружин. Провести исследования так, чтобы максимально понять физику пространственных колебаний винтовых цилиндрических пружин, прицельно исследовать физические явления и расчетные артефакты, связанные с колебаниями пружин. Для этого варьировать параметры пружин, создавая условия для проявления тех или иных явлений. Так задача исследования колебаний пружин ещё не ставилась.
Например, исследовать частоты и формы колебаний при близком совпадении частот (взаимная модуляция, точность расчетов). При близком совпадении поперечных частот реализуется одна из них [2]: так ли это, если так, то какая и почему? Субрезонансы, предварительно, образуются только к основным частотам пространственных продольных, поперечных и крутильных колебаний, т.е. низшим частотам (там, где частотный спектр более линеен) – так ли это? Имеются ли гиперрезонансы и комбинационные частоты? Особые частоты (моды с нулевой групповой скоростью) (рисунок 3): их роль, влияние на другие частоты, наличие в экспериментальном частотном спектре? Один из авторов обнаружил явление резкого уменьшения амплитуды резонансных колебаний при близком совпадении основных частот пространственных продольных, поперечных и крутильных колебаний при кинематическом нагружении и назвал это явление «размыв резонанса» [7], исследовать его: так ли это, насколько количественно, механизм процесса? Здесь на руку играет то, что в пружинах до таких явлений проще «дотянуться».
Для реализации вышеуказанных идей авторами разработаны и изготовлены опытные пружины и установки для крепления пружин. В настоящее время приступаем к непосредственным экспериментам.
В приведенной статье теоретическая часть и постановка задачи принадлежат Полищуку А.Д., расчет опытных пружин, их изготовление, проектирование и изготовление установки выполнены совместно обоими соавторами.
Список литературы:
1.Полищук Д.Ф. Обобщённая теория цилиндрических пружин Ижевск: Изд-во Удм. ун-та, 1992. 216 с.
2.Полищук А.Д., Полищук Д.Ф. Экспериментальная интеграционная механика. Москва-Ижевск.: Институт компьютерных исследований; НИЦ «Регулярная и хаотическая динамика», 2008. 124 с.
3.Товстик П.Е. Асимптотический метод интегрирования уравнений колебаний пружин // Вестник ЛГУ , 1962. - вып. № 7. С. 119—134.
4.Хвингия М.В. Вибрации пружин. М.: Машиностроение. 1969. 286 с.
5.Della Pietra L, Della Valle S. On the dynamic behaviour of axially excited helical springs. Meccanica, 1982. 17:31.
6.Mottershead J.E. Finite elements for dynamical analysis of helical rods. International Journal of Mechanical Sciences, 1980; 22:267.
7.Polishchuk A.D. Interconnected spatial vibrations of helical springs.// Proceedings of the XXXIV Summer School Advanced Problems in Mechanics – 2006. - pp. 413—422.
дипломов


Оставить комментарий