Статья опубликована в рамках: XI Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 25 июня 2012 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МЕТОД РЕКУРРЕНТНОГО ПОСТРОЕНИЯ ФАКТОРИАЛЬНЫХ ФОРМ ЦЕПЕЙ В ОКРЕСТНОСТИ СТАТИСТИЧЕСКОГО ГЛОБАЛЬНОГО ОПТИМУМА
Чистик Игорь Константинович
аспирант кафедры ВТ и АСУ, г. Краснодар
E-mail: chistik1986@list.ru
METHOD OF RECURRENT CREATION OF FACTORIAL FORMS OF CHAINS (FFC) IN A VICINITY OF A STATISTICAL GLOBAL OPTIMUM (SGO)
Igor Chistik
Post-graduate student, chair of CF and ACS,
Krasnodar
АННОТАЦИЯ
Статья посвящена актуальным вопросам построения интеллектуальных систем, обеспечивающих эффективное решение прикладных NP-полных задач оптимального потребления ресурсов произвольной природы путём локализации субоптимальных решений в окрестности статистического глобального оптимума (СГО). Рассматривается метод рекуррентного построения ФФЦ в окрестности СГО. Аналогов данному методу построения окрестности СГО на основе прогрессии ФФЦ не найдено.
ABSTRACT
Article is devoted to topical issues of creation of the intellectual systems providing the effective solution of applied NP full tasks of optimum consumption of resources of any nature by localization of suboptimum decisions in a vicinity of a statistical global optimum (SGO). The method of recurrent creation of FFC in SGO vicinity is considered. Analogs this method of creation of a vicinity of SGO on the basis of a progression of FFC it is not found.
Ключевые слова: окрестность; эвристика; гармоника; функция.
Keywords: vicinity; heuristics; harmonica; function.
1. Метод рекуррентного построения ФФЦ в окрестности СГО. Основные параметры и характеристики метода
Метод рекуррентного построения ФФЦ в окрестности СГО заключается в формировании СГО в виде объединения N гармоник 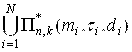 , каждая из которых определяется тройкой параметров mi, ti, di. Наименьшая вероятность цепи в гармонике с наименьшим номером и нулевым смещением определяет ширину окрестности e. Остальные гармоники определяют изменяемый параметр ширины x. Величина N задаётся экспериментально, исходя из требуемой точности, 1 £ N £ k. Выбор значений троек элементов указанной окрестности СГО предлагается делать исходя из свойств локализации субоптимальных решений. Эвристика выбора представляется в следующем виде:
, каждая из которых определяется тройкой параметров mi, ti, di. Наименьшая вероятность цепи в гармонике с наименьшим номером и нулевым смещением определяет ширину окрестности e. Остальные гармоники определяют изменяемый параметр ширины x. Величина N задаётся экспериментально, исходя из требуемой точности, 1 £ N £ k. Выбор значений троек элементов указанной окрестности СГО предлагается делать исходя из свойств локализации субоптимальных решений. Эвристика выбора представляется в следующем виде:
m1 = 1, t1 = 0, d1 = N,
mi+1 = mi, t i+1 = D i+1, d i+1 = d i – 1.
Здесь первая гармоника с нулевым смещением определяет ширину окрестности e, первые гармоники со смещениями t > 0 влияют на величину x. На рисунке 1 и в таблице 1 приведены окрестность СГО для N = 3 при поиске субоптимальных цепей p(5,6), а также параметры гармоник.
Так как рассмотренный метод при переборе решений использует только эвристическую рекуррентную функцию,
![]() , (1)
, (1)
где ![]() - окрестность СГО, Δm - шаг арифметической прогрессии, d объём поиска, f – ФФЦ,
- окрестность СГО, Δm - шаг арифметической прогрессии, d объём поиска, f – ФФЦ,
возвращающую преимущественно субоптимальные ФФЦ, и не использует какую бы то ни было функцию оценки, то данный метод следует отнести к эвристическим псевдослучайным методам.
Таблица 1
Гармоники ![]() и их параметры
и их параметры
|
i |
mi |
Di |
ti |
di |
|
|
1 |
1 |
6 |
0 |
3 |
{0, 6, 12} |
|
2 |
1 |
6 |
2 |
2 |
{2, 8} |
|
3 |
1 |
6 |
1 |
1 |
{1} |
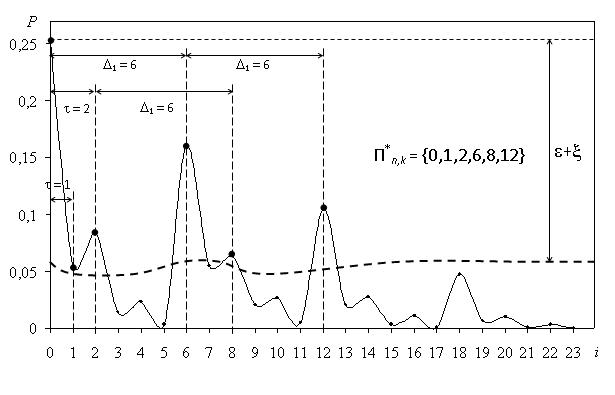
Рисунок 1 – окрестность СГО
![]()
2. Достоинства и недостатки метода рекуррентного построения ФФЦ в окрестности СГО
Достоинства метода:
1) Порядок построения цепей по увеличению ФФЦ характеризуется минимальными вычислительными затратами по сравнению с любым другим методом построения равноудалённых на дереве поиска цепей.
2) Возможность произвольного останова поиска либо по времени, либо по достижению заданного значения функции веса, либо по количеству просмотренных вариантов решений.
Недостатки:
1) Отсутствие управления при выборе локального решения, что характерно для методов случайного поиска.
2) Точность решения зависит от заданного объёма поиска и времени поиска.
3) Окрестность СГО является гибкой (e + x)‑окрестностью, в которой величина x зависит от правильного выбора вида рекуррентной эвристической формулы. Задание эвристической формулы (1) с параметрами i-х гармоник i > 1, не достаточно точно отражающими локализацию субоптимальных решений в пространстве поиска, ведёт к увеличению изменяемого параметра x ширины окрестности e + x. При этом данное увеличение является величиной малого порядка, так как 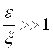 .
.
Следует заметить, что аналогов данному методу построения окрестности СГО на основе прогрессии ФФЦ не найдено. Поэтому для оценки эффективности предложенного метода рекуррентного построения ФФЦ выбраны эвристические методы Шермана-Рейтера и Лина, специально разработанные для минимизации веса цепей p(n, n + 1). Метод Шермана-Рейтера просматривает n+1 вариантов решений путём 2-замен в начальном решении, роль которого, как правило, играет СГО; метод Лина просматривает 3×n+1 вариантов решений путём 3-замен в начальном решении. Для уравнивания указанных объёмов поиска с методом рекуррентного построения ФФЦ, задающего объём поиска параметром N, величина данного параметра вычислялась исходя из соотношения суммы арифметической прогрессии и величин n+1 и 3×n+1. Таким образом, для известного объёма a = n+1 и a = 3×n+1 параметр N вычислялся по формуле  . Результаты работы алгоритмов сравнивались по среднему за C = 10000 испытаний отношению теоретической оценки веса hinf наилегчайшей цепи для каждого графа к весу hmin цепи, определяемому конкретным алгоритмом:
. Результаты работы алгоритмов сравнивались по среднему за C = 10000 испытаний отношению теоретической оценки веса hinf наилегчайшей цепи для каждого графа к весу hmin цепи, определяемому конкретным алгоритмом:  . Теоретическая нижняя оценка веса hinf определялась как половинная сумма весов двух наилегчайших рёбер, то есть рёбер с рангами r = 0, 1, инцидентных каждой вершине vi исходного графа:
. Теоретическая нижняя оценка веса hinf определялась как половинная сумма весов двух наилегчайших рёбер, то есть рёбер с рангами r = 0, 1, инцидентных каждой вершине vi исходного графа: 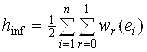 , где wr(ei) - вес ребра ранга r инцидентного вершине vi.
, где wr(ei) - вес ребра ранга r инцидентного вершине vi.
Веса рёбер графа генерировались для каждого опыта случайным образом из интервала [0, 1].На рисунке 2 приведены результаты сравнения эффективности методов рекуррентного построения ФФЦ в окрестности СГО и эвристических методов Шермана-Рейтера и Лина при поиске цепей π(n, n + 1) минимального веса.

Рисунок 2 – Экспериментальное сравнение эффективности метода рекуррентного построения ФФЦ в окрестности СГО и эвристических методов Шермана-Рейтера и Лина при поиске цепей p(n, n + 1) минимального веса
Метод рекуррентного построения ФФЦ при используемой эвристике (1) решает указанную задачу эффективно, но при условии роста n эффективность резко падает. Однако разработанный метод примерно в 1,5 раза эффективнее методов, специально разработанных для решаемой задачи. В связи с этим эвристика (1) требует улучшения для задач большой размерности.
Список литературы:
1.Гашков С.Б., Чубариков В.Н. Арифметика. Алгоритмы. Сложность вычислений. 2-е изд., перераб. – М.: Высш. шк., 2000. – 320 с.
2.Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. – М.: Мир, 1982. – 416 с.
3.Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность: Пер. с англ. – М.: Мир, 1985. – 512 с.
4.Макконелл Дж. Основы современных алгоритмов. 2‑е дополненное издание: Пер. с англ. – М.: Техносфера, 2004. – 368 с.
дипломов


Оставить комментарий