ОКРЕСТНОСТЬ СТАТИСТИЧЕСКОГО ГЛОБАЛЬНОГО ОПТИМУМА. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ХАРАКТЕРИСТИКИ, РАСКРЫВАЮЩИЕ ПОНЯТИЕ ОКРЕСТНОСТИ СТАТИСТИЧЕСКОГО ГЛОБАЛЬНОГО ОПТИМУМА

Чистик Игорь Константинович

аспирант кафедры ВТ и АСУ, г. Краснодар

E-mail:

NEIGHBORHOOD OF A STATISTICAL GLOBAL OPTIMUM. THE MAIN DETERMINATIONS AND THE CHARACTERISTICS UNCOVERING CONCEPT OF NEIGHBORHOOD STATISTICAL GLOBAL OPTIMUM

Igor Chistik

Post-graduate student, chair of CF and ACS,

Krasnodar

АННОТАЦИЯ

В статье раскрывается общий смысл окрестности статистического глобального оптимума (СГО), характеризующие данное понятие параметры, а также наиболее благоприятные условия для вычисления оптимального результата при помощи построения окрестности СГО.

Одной из главных характеристик окрестности СГО является ее ширина. Ширину окрестности необходимо задавать величиной такой малости, при которой мощность множества будет примерно соответствовать прогнозируемому объёму поиска, так как практическое решение задач ограничивается временем и количеством проверяемых решений.

В случае задания большой ширины окрестности СГО при малом времени поиска либо малом объёме, поиск будет неэффективным, так как внутри окрестности СГО поиск упорядочен не по уменьшению вероятности решений, а по увеличению ФФЦ.

ABSTRACT

In article the general sense neighborhoods statistical global optimum (SGO), characterizing given concept parameters, and also optimum conditions for calculation of optimal result by means of creation of neighborhood SGO is uncovered.

One of the main characteristics of a vicinity of SGO is its width. The width of a vicinity is necessary for setting in size of such smallness at which the capacity of a set will correspond to approximately predicted volume of search as the practical solution of tasks is limited to time and number of checked decisions.

In case of a task of big width of a vicinity of SGO at small time of search or small volume, search will be inefficient as in SGO vicinity search is ordered not on reduction of probability of decisions, and on increase in FFСh.

Ключевые слова: окрестность; эвристика; вероятность; оптимум.

Keywords: neighborhood; heuristics; probability; optimum.

1. Основное определение окрестности СГО

Определение 1

Точная e‑окрестность СГО есть множество П_e цепей p_i, вероятность которых меньше вероятности P₀ СГО не более, чем на априорно заданную величину 0 £ e £ P₀

П_e = {p_i | P(p₀) – P(p_i) £ e}.

Величина e является шириной окрестности. На рисунке 1 изображен пример точной e‑окрестности СГО для экспериментальной функции вероятности P(i) оптимальных цепей p_i(5,6). Данная окрестность включает решения (0, 2, 6, 12) в порядке увеличения факториальных форм цепей (ФФЦ). Именно при таком порядке вычислительные затраты достигают минимума. В случае упорядочения точной e‑окрестности СГО по уменьшению вероятности решений (0, 6, 12, 2) вычислительные затраты возрастают при сохранении суммы вероятностей P₀ + P₂ + P₆ + P₁₂ = Const.

2. Граничные значения ширины окрестности

·     При e = 0, точная окрестность СГО содержит одно «Беллмановское» решение для каждого конструктора K_i структур z_i. В данном случае поиск решения сводится к одному из методов динамического программирования, соответствующему используемой эвристике K_i.

·     При e = P₀, точная окрестность СГО включает все решения пространства поиска. В данном случае поиск решения сводится к методу обхода дерева «сначала вглубь» и может быть остановлен либо по времени, либо по количеству проверенных вариантов решений.

Наибольший интерес представляет собой поиск субоптимального решения при e ® 0 для n ® ¥.

Способы задания величины e рассматриваются для каждого метода построения окрестности СГО отдельно.

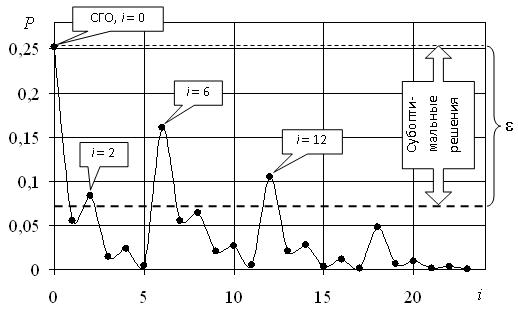
Рисунок 1 – Точная e‑окрестность СГО на упорядоченной по увеличению ФФЦ функции вероятности P(i) оптимальных цепей p_i(5,6)

На данный момент не существует методов построения точной окрестности СГО ввиду сложности построения эвристик, априорно оценивающих величину P_i по рангам цепи p_i = (r₁, r₂, …, r_k). В настоящей статье рассматривается e‑окрестность с изменяемой на величину x шириной, названная (e + x)‑окрестность. Для такой окрестности в работе были построены эвристики, которые позволяют априорно оценить величину P_i по рангам цепи p_i(n, k) = (r₁, r₂, …, r_m) на ранних этапах вычисления веса h(p_i), то есть для m < k.

Определение 2

Гибкая (e + x)‑окрестность СГО есть множество П_ex цепей p_i, вероятность которых меньше вероятности P₀ СГО не более, чем на ширину окрестности 0 £ e + x £ P₀, где x – изменяемый параметр ширины,

П_ex = {p_i | P(p₀) – P(p_i) £ e + x}.

Величина e + x является шириной окрестности. На рисунке 2 изображён пример (e + x)‑окрестности СГО для экспериментальной функции вероятности P(i) оптимальных цепей p_i(5,6). Данная окрестность включает цепи (0, 6, 8, 12, 18) в порядке увеличения ФФЦ.

Определение 3

Реальная (e + x)‑окрестность СГО есть множество П¢_ex ФФЦ, вес которых проверен в ходе поиска, П¢_ex Ì П_ex.

Для (e + x)‑окрестности СГО, изображённой на рисунке 2, возможные варианты реальной (e + x)‑окрестности, то есть реализованной практически, могут быть следующими: П¢_ex = {0,6,8,12,18}, П¢_ex = {0,6,8,12}, П¢_ex = {0,6,8}, П¢_ex = {0,6}, П¢_ex = {0}.

3. Показатели эффективности поиска в окрестности СГО

·     Объём поиска есть количество K проверенных решений из окрестности П_ex СГО, K £ |П_ex|.

·     Приведённый объём поиска есть отношение объёма поиска к ширине окрестности поиска , K £ |П_ex|. Максимальное значение данного показателя позволяет определить объём (либо ширину окрестности) наиболее эффективного поиска при заданной ширине окрестности (либо объёме).

·     Плотность поиска есть отношение объёма поиска к теоретической мощности множества П_n,k всех альтернатив .

·     Приведённая плотность поиска есть отношение объёма поиска к мощности (e + x)‑окрестности СГО . Данный показатель позволяет оценить завершённость проверки всех решений в СГО П_ex.

Рисунок 2 – Гибкая (e + x)‑окрестность СГО на упорядоченной по увеличению ФФЦ плотности распределения вероятности P(i) оптимальных цепей p_i(5,6)

На практике решение задачи ограничивается либо временем, либо количеством проверяемых решений, поэтому ширину окрестности необходимо задавать величиной такой малости, при которой мощность множества П_ex будет примерно соответствовать прогнозируемому объёму поиска K » |П_ex|.

В случае задания большой ширины окрестности СГО при малом времени поиска (либо малом объёме) поиск будет неэффективным, так как внутри окрестности СГО поиск упорядочен не по уменьшению вероятности решений, а по увеличению ФФЦ. Данный случай демонстрируется на рисунке 3, где показано, что для малого объёма поиска K = 5 и выбранной большой ширины окрестности СГО реальная (e + x)‑окрестность П¢_ex = {0,1,2,3,4}. Это является одной из причин неэффективного поиска, так как большая часть решений – {1,3,4} содержит маловероятные цепи. В данном случае, для K = 5, ширина окрестности должна быть уменьшена до такой величины, при которой реализованная на практике окрестность П¢_ex = {0,2,6,8,12} или близкой к ней.

4. Условия линеаризации ширины (e + x)‑окрестности

·     При n ® ¥ параметром x можно пренебречь, так как для максимизации приведённого объёма поиска ширина окрестности должна быть величиной, близкой к нулю e + x ® 0. Данной условие обосновывается тем, что при большой размерности входных данных вероятность СГО мало отличается от вероятности субоптимальных решений, а также тем, что согласно второму свойству пространства поиска решений, – с ростом n вероятность статистического глобального оптимума p₀(n, k) стремится к нулю .

·     Для алгоритмов, использующих останов по времени T (либо по объёму K), в случае большой величины Т (K) можно допустить e = Const, x = 0.

·     Для алгоритмов с приведённой плотностью поиска r¢ = 1 в случае большой ширины окрестности можно допустить e = Const, x = 0.

Так как прикладные задачи, как правило, имеют большую размерность исходных данных, то вышеописанные условия на практике выполняются. Используем свойства пространства поиска для того, чтобы найти эвристики r_i+1 = h^r(s⁽ⁱ⁾), управляющие переходом NP‑полной системы. Посредством данных эвристик недетерминированный переход s⁽ⁱ⁾ ® s⁽ⁱ⁺¹⁾ преобразуется в детерминированный .

Рисунок 3 – Точная e‑окрестность СГО на упорядоченной по увеличению ФФЦ плотности распределения вероятности P(i) оптимальных цепей p_i(5,6)

Список литературы:

1.Касьянов В.Н., Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение. – СПб.: БХВ-Петербург, 2003. – 1104 с.

2.Корн Г, Корн Т. Справочник по математике. Определения, теоремы, формулы. 6‑е изд., стер. – СПб.: Издательство «Лань», 2003. – 832 с.

3.Макконелл Дж. Основы современных алгоритмов. 2‑е дополненное издание: Пер. с англ. – М.: Техносфера, 2004. – 368 с.

4.Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. Алгоритмы и сложность: Пер. с англ. – М.: Мир, 1985. – 512 с.