Статья опубликована в рамках: X Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 28 мая 2012 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
КИНЕМАТИЧЕСКИЙ АЛГОРИТМ КОНТУРНОГО УПРАВЛЕНИЯ МАНИПУЛЯЦИОННЫМ РОБОТОМ В РЕЖИМЕ РЕАЛЬНОГО ВРЕМЕНИ
Стебулянин Михаил Михайлович
канд. техн. наук, доцент, начальник управления подготовки научных кадров, МГТУ “Станкин”, г. Москва
Email: mmsteb@rambler.ru
Синицын Андрей Геннадьевич
аспирант кафедры “Робототехника и мехатроника”, МГТУ “Станкин”, г. Москва
Email:
KINEMATIC PATH CONTROL ALGORITHM FOR INDUSTRIAL ROBOT IN REAL-TIME MODE
Mikhail Stebulyanin
Candidate. Technical. Associate Professor. Head of the MSUT “Stankin” department of scientific personnel training. Moscow
Andrey Sinitsyn
MSUT “Stankin”, “Robotics and mechatronics” subdepartment graduate student. Moscow
АННОТАЦИЯ
В данной работе предложен кинематический алгоритм контурного управления манипуляционными роботами, направленный на оперативное формирование программы движения манипулятора. Приводится математическое обоснование алгоритма и правила настройки параметров уравнения управления. Представлены результаты математического моделирования процесса преследования роботом движущейся цели, подтверждающие эффективность работы алгоритма.
ABSTRACT
We propose a new path control kinematic algorithm for industrial manipulators, which is purposed for real-time control applications. Mathematical proof of the control equation and rules of parameters choice are given in this paper. Basing on the simulation results, which are represented in this paper, we make conclusions about the algorithm’s efficiency.
Ключевые слова: уравнение управления; контурное управление; манипуляционный робот; кинематический алгоритм.
Keywords: control equation; path control; robot manipulator; kinematic control algorithm.
Одной из актуальных задач управления манипуляционными роботами является разработка новых алгоритмов контурного управления, направленных на оперативное формирование желаемого закона движения приводов ![]() . Возможная область применения таких алгоритмов достаточно широка и в первую очередь связана с роботизацией технологических процессов, характеризующихся нечеткой исходной информацией. Так, например, при выполнении роботизированных сварочных операций крупногабаритных заготовок в судостроительном производстве [6, с. 377] или изготовлении мачтовых конструкций [1, с. 33] возникают существенные погрешности расположения стыка свариваемых поверхностей в рабочей зоне манипулятора, в связи с чем, возможности применения традиционных методов off-line программирования ограничены.
. Возможная область применения таких алгоритмов достаточно широка и в первую очередь связана с роботизацией технологических процессов, характеризующихся нечеткой исходной информацией. Так, например, при выполнении роботизированных сварочных операций крупногабаритных заготовок в судостроительном производстве [6, с. 377] или изготовлении мачтовых конструкций [1, с. 33] возникают существенные погрешности расположения стыка свариваемых поверхностей в рабочей зоне манипулятора, в связи с чем, возможности применения традиционных методов off-line программирования ограничены.
Под задачей контурного управления n-звенным манипуляционным роботом будем понимать задачу определения функции обобщенных координат ![]() в зависимости от желаемого закона движения
в зависимости от желаемого закона движения  в физическом пространстве. Кинематический подход заключается в выборе закона управления ошибкой
в физическом пространстве. Кинематический подход заключается в выборе закона управления ошибкой ![]() , называемого уравнением управления, от которого зависят основные показатели качества системы управления: быстродействие, перерегулирование переходных процессов, робастность (
, называемого уравнением управления, от которого зависят основные показатели качества системы управления: быстродействие, перерегулирование переходных процессов, робастность (![]() - фактический закон движения рабочего органа манипулятора).
- фактический закон движения рабочего органа манипулятора).
Уравнение управления ошибкой ![]() выбирается из числа линейных однородных дифференциальных уравнений n-го порядка и в общем случае имеет вид:
выбирается из числа линейных однородных дифференциальных уравнений n-го порядка и в общем случае имеет вид:
 (1)
(1)
где ![]() ,
,![]() ,…,
,…,![]() – постоянные коэффициенты,
– постоянные коэффициенты, 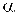 - параметр адаптивной настройки кинематического алгоритма, определяющий скорость переходного процесса.
- параметр адаптивной настройки кинематического алгоритма, определяющий скорость переходного процесса.
При одних и тех же значениях коэффициентов ![]() ,
,![]() ,…,
,…,![]() выполняется следующее соотношение для времени переходного процесса
выполняется следующее соотношение для времени переходного процесса  при
при ![]() и времени переходного процесса
и времени переходного процесса 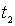 при
при ![]() [5, с. 18] :
[5, с. 18] :
![]() (2)
(2)
Кроме того, характер протекания переходного процесса в системе, описываемой уравнением (1) сильно зависит и от начальных условий 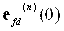 ,
,![]() ,…,
,…, ![]() .
.
Таким образом, возникает задача выбора оптимального по критериям устойчивости и быстродействия уравнения управления.
Рассмотрим задачу выбора коэффициентов уравнения (1) в одномерном пространстве, т. е. для одной из компонент вектора ![]() при выполнении условий:
при выполнении условий:
![]() ,
, ![]() ,…,
,…,![]() ,
,![]() (3)
(3)
Выбор левой части уравнения (1) будем проводить из числа типовых нормированных полиномов (биномиальных и колебательных), используемых при проектировании желаемых передаточных функций замкнутых систем управления в алгебраическом методе синтеза [5, с. 15].
Рассмотрим типовые нормированные полиномы ![]() , используемые для синтеза передаточных функций замкнутых систем управления, не обладающих нулями.
, используемые для синтеза передаточных функций замкнутых систем управления, не обладающих нулями.
Имеет смысл использовать только полиномы второго порядка, т. к. увеличение порядка n приводит к снижению быстродействия системы управления и повышению вычислительной сложности алгоритма.
Показатели качества переходной функции системы управления, описываемой передаточной функцией вида  и показатели качества переходного процесса по ошибке
и показатели качества переходного процесса по ошибке  при выборе уравнения управления в виде
при выборе уравнения управления в виде 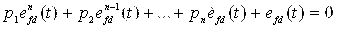 совпадают при выполнении условия (3).
совпадают при выполнении условия (3).
При невыполнении условия (3) показатели качества переходного процесса в системе, описываемой уравнением ![]() , не соответствуют аналогичным характеристикам переходной функции системы с передаточной функцией вида
, не соответствуют аналогичным характеристикам переходной функции системы с передаточной функцией вида  . В связи с чем, возникает отдельная задача выбора коэффициентов
. В связи с чем, возникает отдельная задача выбора коэффициентов ![]() (
(![]() ) уравнения управления (1) при ненулевых начальных скоростях.
) уравнения управления (1) при ненулевых начальных скоростях.
Данный выбор проведем на основе сравнения переходных процессов с нулевыми и ненулевыми начальными условиями по скорости. В качестве критерия для определения оптимальных значений коэффициентов уравнения (1) примем среднеквадратичную функцию невязки указанных переходных процессов:
![]() , (4)
, (4)
где ![]() - эталонный переходный процесс при нулевых начальных условиях по скорости и значениях коэффициентов уравнения управления
- эталонный переходный процесс при нулевых начальных условиях по скорости и значениях коэффициентов уравнения управления ![]() ,
, ![]() ;
;![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Предлагаемый критерий подлежит минимизации.
При указанной форме критерия ![]() (4) аналитическое решение системы двух уравнений
(4) аналитическое решение системы двух уравнений
 (5)
(5)
относительно ![]() и
и ![]() является затруднительным. Однако при заданных начальных условиях
является затруднительным. Однако при заданных начальных условиях ![]() ,
, ![]() найти оптимальные значения коэффициентов
найти оптимальные значения коэффициентов ![]() ,
, ![]() можно, используя численные методы. В данной работе для решения (5) использовалась стандартная функция fminsearch среды Matlab.
можно, используя численные методы. В данной работе для решения (5) использовалась стандартная функция fminsearch среды Matlab.
Поэтому для приближенного нахождения зависимостей ![]() и
и ![]() воспользуемся методом наименьших квадратов (МНК). Зависимость оптимальных значений
воспользуемся методом наименьших квадратов (МНК). Зависимость оптимальных значений ![]() и
и ![]() от величин начальных условий опишем моделью, представляющей собой комбинацию линейной, квадратичной и кубической форм:
от величин начальных условий опишем моделью, представляющей собой комбинацию линейной, квадратичной и кубической форм:

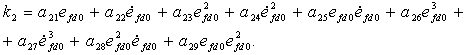
Исходными данными для решения поставленной задачи с помощью МНК является множество значений ![]() и
и ![]() , полученных с использованием вышеупомянутой функции в конечном множестве точек
, полученных с использованием вышеупомянутой функции в конечном множестве точек ![]() . Ограничимся рассмотрением начальных условий в диапазоне:
. Ограничимся рассмотрением начальных условий в диапазоне: ![]() ,
, ![]() . Данные представлены в табл. 1.
. Данные представлены в табл. 1.
Таблица 1.
Оптимальные значения коэффициентов уравнения управления
|
|
|
|
||||||||||
|
-0,5 |
-0,4 |
-0,3 |
-0,2 |
-0,1 |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
||
|
0,2 |
|
4,35 3,34 |
4,35 3,34 |
4,35 3,34 |
4,35 3,34 |
4,35 3,34 |
1,00 1,5 |
0,55 1,34 |
0,40 1,25 |
0,3 1,08 |
0,25 1,00 |
0,25 1,00 |
|
0,4 |
|
4,35 3,34 |
4,35 3,34 |
4,35 3,34 |
4,35 3,34 |
1,65 1,80 |
1,00 1,5 |
0,70 1,39 |
0,55 1,34 |
0,45 1,30 |
0,40 1,25 |
0,35 1,17 |
|
0,6 |
|
4,35 3,34 |
4,35 3,34 |
4,35 3,34 |
2,10 2,03 |
1,35 1,65 |
1,00 1,5 |
0,80 1,41 |
0,65 1,37 |
0,55 1,34 |
0,45 1,33 |
0,41 1,27 |
|
0,8 |
|
4,35 3,34 |
4,35 3,34 |
2,41 2,19 |
1,66 1,81 |
1,24 1,60 |
1,00 1,5 |
0,82 1,43 |
0,71 1,39 |
0,59 1,36 |
0,52 1,34 |
0,46 1,33 |
|
1 |
|
2,98 2,76 |
2,61 2,32 |
1,88 1,92 |
1,44 1,69 |
1,18 1,59 |
1,00 1,5 |
0,86 1,45 |
0,74 1,41 |
0,66 1,38 |
0,58 1,36 |
0,52 1,34 |
Сравнивая переходные процессы ![]() и
и ![]() , обладающие равными по модулю начальными условиями
, обладающие равными по модулю начальными условиями ![]() и
и ![]() соответственно, из общего решения уравнения (1) с колебательным полиномом 2-го порядка в левой части
соответственно, из общего решения уравнения (1) с колебательным полиномом 2-го порядка в левой части

можно заметить, что если ![]() , то
, то ![]() . Это означает, что переходные процессы
. Это означает, что переходные процессы ![]() и
и ![]() обладают одинаковыми характеристиками. Поэтому множество значений
обладают одинаковыми характеристиками. Поэтому множество значений ![]() в табл. 1 можно ограничить только положительными величинами.
в табл. 1 можно ограничить только положительными величинами.
Используя известную процедуру МНК [2, с. 343], получим следующие значения коэффициентов:
![]()
![]()
![]()
![]()
В пространстве возникает задача векторного управления, поэтому данный подход предполагает выбор разных значений коэффициентов ![]() ,
, ![]() для управления различными компонентами вектора ошибки
для управления различными компонентами вектора ошибки ![]() ,
, ![]() ,
, ![]() . В этом случае вместо скалярных коэффициентов
. В этом случае вместо скалярных коэффициентов ![]() ,
, ![]() в уравнении (1) используются диагональные матрицы вида:
в уравнении (1) используются диагональные матрицы вида:
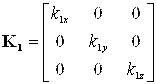 ;
;
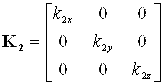 .
.
Далее на основе выбранного уравнения управления вида
![]() (6)
(6)
рассмотрим задачу формирования закона ![]() , реализующего желаемый закон движения
, реализующего желаемый закон движения ![]() в физическом пространстве для 6-звенного манипулятора (
в физическом пространстве для 6-звенного манипулятора (![]() ).
).
Производная вектора ошибки ![]() составит:
составит:
![]() . (7)
. (7)
Векторы скоростей ![]() и
и ![]() связаны уравнением:
связаны уравнением:
![]() , (8)
, (8)
где ![]() - Якобиева матрица функции
- Якобиева матрица функции ![]() , которую можно представить в виде блочной матрицы:
, которую можно представить в виде блочной матрицы:  , где
, где ![]() ,
, ![]() - якобианы функций перемещения и ориентации соответственно.
- якобианы функций перемещения и ориентации соответственно.
Продифференцировав (8) с учетом (7), получим желаемый закон изменения обобщенных ускорений манипулятора, соответствующий движению ![]() в физическом пространстве:
в физическом пространстве:
![]() (9)
(9)
После подстановки уравнения управления (6) окончательно получим:
![]() (10)
(10)
При двукратном интегрировании уравнения (10) вычисляется искомая функция времени ![]() .
.
Параметром настройки движения преследования целевого триэдра является угловая частота ![]() свободных колебаний звена (6).
свободных колебаний звена (6).
Введем управление величиной ![]() , обеспечивающее монотонное убывание функции
, обеспечивающее монотонное убывание функции ![]() – угла между векторами
– угла между векторами ![]() и
и ![]() . Выберем следующий критерий качества процесса преследования:
. Выберем следующий критерий качества процесса преследования:
![]() . (11)
. (11)
Выражая ![]() через скалярное произведение векторов
через скалярное произведение векторов ![]() и
и ![]() , преобразуем неравенство (11) к виду:
, преобразуем неравенство (11) к виду:
![]() , (12)
, (12)
где 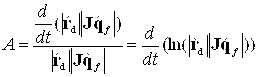 .
.
Из уравнений (7) и (8) выразим вектор фактических обобщенных скоростей:
![]() (13)
(13)
С учетом (10) и (13) из (12) получим следующее квадратичное неравенство относительно ![]() :
:
![]() , (14)
, (14)
где ![]() ;
; ![]() ;
; ![]() .
.
Оптимальная величина ![]() на каждом такте управления рассчитывается в зависимости от значений младшего
на каждом такте управления рассчитывается в зависимости от значений младшего ![]() и старшего
и старшего ![]() корня уравнения
корня уравнения ![]() .
.
Величина ![]() задает динамику управления. Следует сказать, что завышенные значения
задает динамику управления. Следует сказать, что завышенные значения ![]() приводят к перегрузке по потребной мощности движения преследования. Кроме того, величина
приводят к перегрузке по потребной мощности движения преследования. Кроме того, величина ![]() должна быть согласована с возможностями следящего привода.
должна быть согласована с возможностями следящего привода.

Рис. 1. Структура математической модели.
Для оценки эффективности применения разработанного алгоритма было проведено компьютерное моделирование его работы. Структура математической модели представлена на рис. 1. На схеме введены следующие обозначения:
1 – блок расчета программных значений обобщенных ускорений на основании уравнения (5), 2 и 3 – блоки расчета якобиана и его первой производной по времени недифференциальным способом [4, с. 121]; 4 – блок решения прямой задачи кинематики; 5 – блок, моделирующий влияние динамических свойств приводов на отработку программного закона изменения обобщенных координат; 6 – блок расчета оптимальных значений обратной постоянной времени ![]() в соответствии с рассмотренным алгоритмом; 7 – начальные условия для функции
в соответствии с рассмотренным алгоритмом; 7 – начальные условия для функции ![]() .
.
Для учета влияния динамических свойств привода на процесс управления манипулятором была использована модель трехконтурного следящего привода постоянного тока, замкнутого по положению. При выборе для каждого из контуров тока, скорости и положения стандартных настроек на оптимум по модулю [3, с. 17] данный привод может быть приближенно описан передаточной функцией эквивалентного колебательного звена:
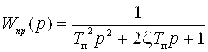 ,
,
где ![]() - постоянная времени, а
- постоянная времени, а ![]() - коэффициент демпфирования.
- коэффициент демпфирования.
Моделирование проводилось для трехзвенного манипулятора c кинематической схемой транспортных степеней подвижности робота KUKA KR-30-3.
В качестве примера рассмотрим случай, когда задан желаемый закон движения полюса рабочего органа:

Результаты моделирования при ![]() c графически представлены на рис. 2—3.
c графически представлены на рис. 2—3.
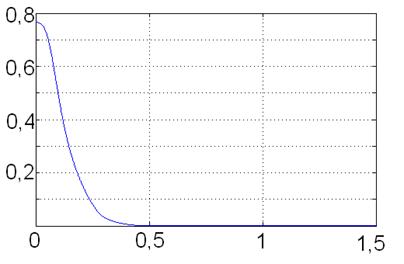
Рис. 2. Изменение нормы вектора ![]()
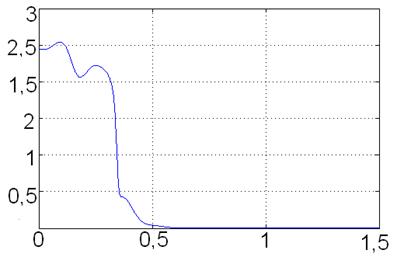
Рис. 3. Изменение угла ![]()
Выводы
Переходные процессы, представленные на рис. 2—3 свидетельствуют об устойчивости движения манипулятора под управлением разработанного кинематического алгоритма. Выбор значений ![]() в соответствии с критерием (11) позволяет повысить монотонность кривой
в соответствии с критерием (11) позволяет повысить монотонность кривой ![]() на протяжении большей части переходного процесса при сохранении высокого быстродействия. Возрастание угла
на протяжении большей части переходного процесса при сохранении высокого быстродействия. Возрастание угла ![]() на некоторых фазах переходного процесса объясняется влиянием динамики приводов исполнительной системы робота и невозможностью удовлетворения условия (11) при определенном сочетании значений коэффициентов неравенства (14).
на некоторых фазах переходного процесса объясняется влиянием динамики приводов исполнительной системы робота и невозможностью удовлетворения условия (11) при определенном сочетании значений коэффициентов неравенства (14).
Таким образом, применение представленного метода оперативного формирования закона движения приводов ![]() позволяет произвести адаптивную настройку алгоритма в зависимости от начальных условий при отсутствии априорной информации о целевом законе движения. Небольшой объем вычислений, предусмотренных данной методикой, делает возможным проводить расчет коэффициентов уравнения управления в режиме реального времени.
позволяет произвести адаптивную настройку алгоритма в зависимости от начальных условий при отсутствии априорной информации о целевом законе движения. Небольшой объем вычислений, предусмотренных данной методикой, делает возможным проводить расчет коэффициентов уравнения управления в режиме реального времени.
Список литературы:
1.Алпеева Т.В., Котельников А.А. Роботизированное производство сварных ферм для мачтовых сооружений // Сварочное производство. 2007. № 1. C. 33—36.
2.Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров: учеб пособие. – М.: Высш. шк., 1994 - 544 с.
3.Башарин А.В., Новиков В.А., Соколовский Г.Г. Управление электроприводами: Учебное пособие для вузов. – Л. Энергоиздат. Ленингр. отд-ние, 1982. – 392 с.
4.Зенкевич С.Л., Ющенко А.С. Управление роботами. Основы управления манипуляционными роботами: Учеб. Для вузов – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. – 400 с.
5.Ким Д.П. Определение желаемой передаточной функции при синтезе систем управления алгебраическим методом // Мехатроника, автоматизация, управление. 2011. № 5. С. 15—21.
6.M.H. Ang Jr., W. Lin A, S-Y Lim. Walk-Trough Programmed Robot for Welding in Shiptards // Industrial Robot. Vol. 26, No. 5, 1999, pp. 377—388.
дипломов




Оставить комментарий