КЛАСТЕРИЗАЦИЯ ДАННЫХ ГИПЕРСПЕКТРАЛЬНОГО ИЗОБРАЖЕНИЯ ПУТЕМ ПОСТРОЕНИЯ ДИФФУЗНОЙ КАРТЫ

Колтырин Артур Николаевич

инженер отдела проектирования и мониторинга разработки южной группы месторождений, Филиал ООО "ЛУКОЙЛ-Инжиниринг" "ПермНИПИнефть" в городе Перми,

e-mail:

HYPERSPECTRAL IMAGING DATA CLUSTERING BY CONSTRUCTING A DIFFUSION MAP

Arthur Koltyrin

engineer in the design and monitoring of the development of the southern group of fields, Branch of JSC "LUKOIL-Engineering", "PermNIPIneft" in the city of Perm

Аннотация

Одной из проблем обработки гиперспектральных изображений является выделение значимых данных. Эта задача решаются путем классификации. Для решения задач классификации, предлагается построение отображения, при котором спектры различных поверхностей местности, связанные с различными материалами, разделятся явно. В рассматриваемом подходе мы опираемся на метод «диффузных карт». Основная идея в том, что многомерные данные проецируются в математическое многообразие малой размерности с сохранением взаимных отношений между данными. Описывается диффузный процесс, который выявляет скрытые закономерности, существующие между спектрами, разделяющие различные слои бакграунда. Модель, основана на случайном блуждании по графу. Случайное блуждание разделяет всю область на отдельные кластеры, которые обусловлены скрытыми взаимосвязями между элементами множества. В результате применена техника случайных процессов в Марковских цепях для разделения кластеров.

Abstract

One of the problems of processing hyperspectral imaging is the identification of significant data. This problem is solved by means of classification. In order to solve classification problems, it is proposed the construction of maps, in which the spectra of different surfaces areas associated with different materials, is clearly divided. In this approach, we rely on the method of "diffusion map". The basic idea is that the multidimensional data are projected into the mathematical variety of small dimension while preserving the mutual relations between the data. We describe a diffuse process that reveals hidden patterns that exist between the spectra of separating the different layers of the background. The model is based on a random walk on a graph. Random walk divides the region into separate clusters, which are caused by hidden relationships between elements of the set. As a result of applied techniques of random processes in Markov chains for the separation of clusters.

Ключевые слова: диффузная карта; кластеризация; гиперспектральное изображение

Keywords: diffusion map; clustering; hyperspectral imaging

Гиперспектральное изображение - это куб данных, который включает в себя пространственную информация (2D) об объекте, дополненную спектральной информацией (1D) по каждой пространственной координате. Иными словами, каждой точке изображения соответствует спектр, полученный в этой точке снимаемого объекта.

Одной из основных задач обработки гиперспектральных изображений является распознавание неопределенных зон местности как принадлежащих тому или иному известному классу.

Технология распознавания представлена основным набором алгоритмов: AdaBoost, SVM, Нейронные сети, Linear Discriminate Analysis. Проанализировав данные алгоритмы можно сделать вывод что, существующие методы распознавания неопределенных зон гиперспектрального изображения не являются столь эффективными. Поэтому решение задач распознавания неопределенных зон гиперспектральных изображений остаются актуальными.

В нашем случае, решение задач распознавания неопределенных зон гиперспектрального изображения предлагается построить такое отображение, при котором спектры различных поверхностей местности, связанные с различными материалами, разделятся явно.

В рассматриваемом подходе мы будем опираться на метод «диффузных карт» [3].

Этот метод впервые применялся для моделирования трехмерных объектов на базе множества представлений объекта двумерными проекциями (фотографиями). Суть метода заключается в том, что многомерные данные проецируются в математическое многообразие малой размерности с сохранением взаимных отношений между данными. При этом топология многообразия моделирует различие между проекциями. То есть, вариация данных описывается многообразием, выстраиваемым диффузной картой. В случае, когда многообразие трехмерно, оно является трехмерной моделью проекций.

В этой статье мы опишем диффузный процесс, который выявит скрытые закономерности, существующие между спектрами, разделяющие различные слои бакграунда.

Модель, которую мы предлагаем, основывается на случайном блуждании по графу.

Обозначим

Множество объектов, представленных многомерными векторами. Первый индекс обозначает нумерацию объектов в классе, второй индекс нумерует сами классы.

Каждый объект является многомерным вектором размерности n.

Построим граф

   (1)

где множество вершин V соответствует объектам

а множество ребер

- мера локальной близости между векторами, индуцированной нормой L₂.

Данная картина может быть проиллюстрирована рисунком 1.

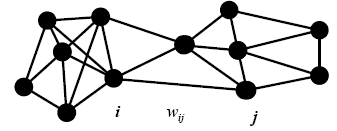
Рисунок 1. граф (1)

На рисунке 1 представлен граф (1). Вершины - объекты системы, ребра - наличие локальной близости между объектами в норме L₂.

Мы инициализируем случайное блуждание точки по графу (1). Блуждание по графу происходит в областях сгущения плотности, поскольку вероятности перехода из узла в узел в плотных участках больше, чем переход из одной точки сгущения в другую [5].

Такое блуждание выделяет кластеры, как области наиболее вероятного нахождения точки при случайном блуждании.

Таким образом, случайное блуждание разделяет всю область V на отдельные кластеры, которые обусловлены скрытыми взаимосвязями между элементами множества I.

Теперь мы дадим более формальное аксиоматическое определение весовых функций, связанных с ребрами графа (1). Функция  определяется как такое отношение локальной близости между вершинами графа, обладающее следующими свойствами. Для всех  весовая функция обладает следующими свойствами:

1.  Симметричность.

2.  Неотрицательность.

3.  Свойство разреженности. Пусть задано вещественное положительное число . Тогда в случае  мы имеем , в противном случае, если , выполняется свойство .

Параметр ε задает локальную структуру окрестности. Функция  задает локальную геометрию подобия пары объектов внутри окрестности радиуса ε.

Как правило, в качестве функции  выбирается «гауссовское ядро» [1].

 (2)

Теперь опишем формально случайный процесс блужданий по графу (1).

Определим вес каждой вершины в графе

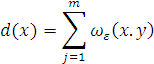
Нормализуем весовые функции  как строки стохастической Марковской матрицы. Более формально, рассмотрим матрицу

определенную как

Величина  может быть интерпретирована, как вероятность перехода из точки x в точку Y за один шаг. Определим теперь вероятность перехода из X в Y за время t . Матрица, составленная из элементов , задает разбиение графа на кластеры при стремлении параметра t к бесконечности [4].

Действительно, если точка находилась в позиции x, то за большое число шагов с наибольшей вероятностью случайное блуждание приведет в те вершины, которые образуют один кластер с x. Таким образом, все точки y, для которых  близко к 1, образуют один кластер с x. При этом точки Y, относящиеся к другому кластеру, будут отделены от x свойством близости к 0 функции  [6].

Рисунок 2 иллюстрирует эффективность разделения перемешанных известных кластеров. Если сгенерировать данные как два сцепленных друг с другом кольца (обозначенных красным и зеленым цветом), то никакие известные линейные методы их явно разделить не смогут. Тем не менее случайное блуждание по графу, представленному этими кольцами, логически их способно разделить, поскольку при случайном блуждании вероятность оставаться внутри одного и того же кольца больше, чем вероятность перейти из одного кольца в другое.

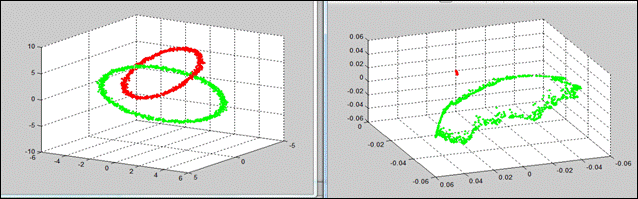
Рисунок 2. Демонстрация эффективности разделения классов при помощи диффузных карт.

Например, для векторов, представленных на рисунке 3, очевидна структура принадлежности группы справа и слева к разным кластерам.

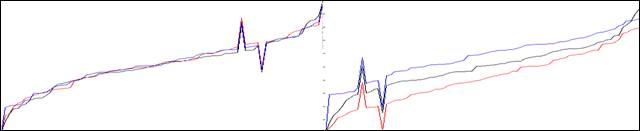
Рисунок 3. Две группы спектров, представленные графиками

Как было показано в [2], диффузное расстояние  может быть вычислено по следующей формуле

где λ1, λ2, ..λm - собственные числа матрицы P, такие что

а ψ1, ψ2,… ψm - соответствующие им собственные векторы.

Отбросив теперь члены при собственных числах, близких к 0 и оставив первые w самых существенных слагаемых, приходим к тождеству

Определим отображение

Нетрудно видеть, что оно обладает следующими свойствами:

• Отображение происходит в пространство размерности w.
• Отображение не является линейным.
• Расстояние между образами точек равно диффузному расстоянию, то есть, вероятности попасть из точки x в точку y при случайном блуждании по графу (1) за время t.

В результате мы построили отображение, при котором спектры связанные с различными материалами, разделяются явно. Данное отображение будем называть «диффузной картой». Применена техника случайных процессов в Марковских цепях для разделения кластеров и выявления взаимосвязей между данными, а также представления кластеров в пространстве малой размерности. Результаты применение показаны на рисунках 4 и 5. Показано разделение кластеров после применения диффузных карт. На рисунках 4 и 5 одним цветом отмечены спектры для одного и того же участка бакграунда. Видно, что в результате разнонаправленности и зашумленности спектров кластеры полностью перемешаны и классификация по ним невозможна. Техника предусматривает отображение спектров в виртуальное пространство отношений, и после понижения размерности, пространство спектров проецируется в трехмерное пространство, где образы спектров, относящихся к одному материалу, хорошо разделены.

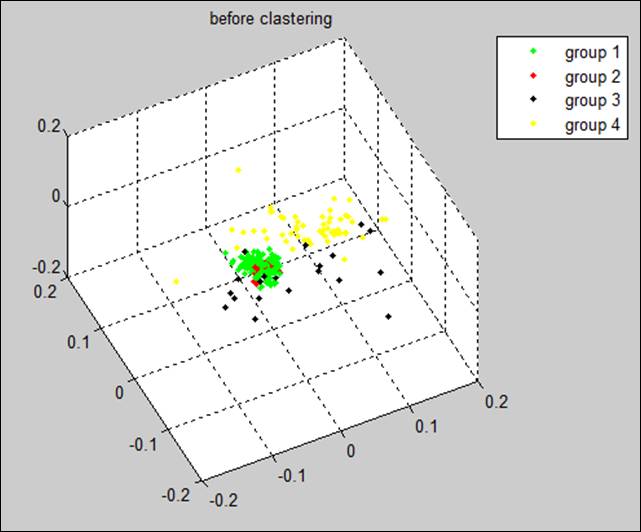
Рисунок 4. Визуализация трех случайно выбранных длин волн гиперспектрального изображения.

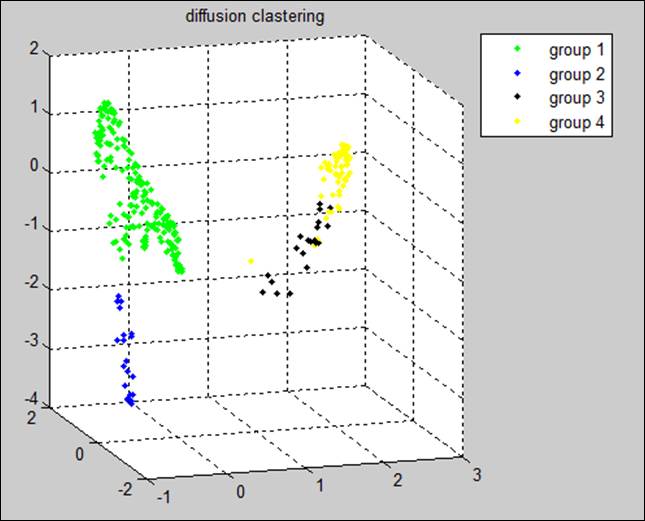
Рисунок 5. Визуализация спектров после применения диффузных карт.

Список литературы:

1.Attias H.. Independent factor analysis. Neural Computation, 11(4):803-851, 1999.

2.Averbuch, M. Zheludev, Sensor analysis algorithms for target recognition, School of Computer Science, Tel Aviv University, Israel, 2009.

3.Coifman R., Stephane L. Diffusion maps, Appl. Comput. Harmon. Anal, Mathematics Department, Yale University, New Haven, CT 06520, USA

4.Chen C.H. and Zhang X.. Independent component analysis for remote sensing study. In Proc. of the SPIE Symp. on Remote Sensing Conference on Image and Signal Processing for Remote Sensing V, volume 3871, pages 150-158, 1999.

5.Generalov, M., Zheludev V., Simultaneous Decompositions of Projective Modules over Bounded Dedekind Prime Rings, International Algebra Faddeev Memorial Conference, Abstracts, 1997, 48.

6.Zheludev V., Tiling of Decomposable Groups by Translations of Finite Set, Journal Murmansk Region Conference, 1999.