ПРОГНОЗИРОВАНИЕ РАБОЧЕЙ НАГРУЗКИ ПЛАНИРОВЩИКА ЗАДАЧ ПУТЕМ ВЫЯВЛЕНИЕ ЦИКЛИЧЕСКИХ ЗАКОНОМЕРНОСТЕЙ

Гриценко Андрей Владимирович

аспирант, Ставропольский ГУ, г. Ставрополь

E-mail:

1. Введение

Широкое использование распределенных вычислительных систем повлекло за собой сначала разработку различных алгоритмов планирования работ и распределения ресурсов, а потом и появление огромного количества ПО, использующего эти алгоритмы. Сейчас рынок DRMS(distributedresourcemanagementsystem) представлен как разработками таких широко известных компаний как AdaptiveComputing(Moabи Maui) и Oracle(OracleGridEngine), так и продукцией более мелких компаний [2]. Несмотря на все внешние различия этих программных продуктов, между ними есть одно сходство – при построении расписания алгоритмы этих продуктов учитывают только те работы, которые на данный момент были добавлены в очередь. В работе [1] дается обоснование точки зрения, согласно которой использование при составлении расписания данных только о текущих работах может являться недостатком. В частности в этой работе указывается, что бывают случаи, когда одна и та же задача может запускаться с определенной периодичностью, и выдвигается предположение, что возможность использования методов прогнозирования в алгоритмах составления расписания в таких случаях могло бы значительно повысить общую эффективность DRMS.

2. Статистический анализ XLSTAT

Одной из причин, почему методы прогнозирования до сих пор не использовались в планировщиках задач, является распространенное мнение, что процесс назначения работ является абсолютно случайным и из-за большого количества пользователей принимающих участие в этом процессе по своим свойствам напоминает белый шум.

Для проверки этого предположения использовался программный продукт XLSTAT, надстройка для Microsoft Office Excel, предоставляющая широкий набор функций для статистического анализа временных рядов [4, 5]. В качестве исходных данных был использован временной ряд, который был получен при анализе данных работы вычислительного кластера Ставропольского государственного университета, и в котором были выявлены продолжительные циклы. Параметрами этого ряда являются дата и время назначения задачи, количество требуемых процессоров и предполагаемое время выполнения задачи.

Прежде всего, из начального временного ряда было выделено два одномерных ряда: ряд, значениями которого является количество запрашиваемых работой процессоров (Procs), и ряд содержащий продолжительность выполнения задачи в часах (Time).

Далее оба этих одномерных ряда были подвергнуты ряду тестов, выполняемых встроенными функциями XLSTAT: Descriptiveanalysis(описательный анализ) [4] и NormalityTests(Нормальные тесты) [5].

Таблица 1.

Результат применения функции XLSTATDescriptiveanalysisк временным рядам Procsи Time

Функция Descriptiveanalysisиспользует тесты Харки-Бера (Jarque-Bera), Бокса-Пирса (Box-Pierce), Льюнга-Бокса (Ljung-Box) и МакЛеода-Ли (McLeod-Li), строит гистограммы частот и автокоррелограммы.

Тест Харки-Бера, использующийся и функцией NormalityTests, основан на сравнении коэффициентов асимметрии и эксцесса и вычисляет возможность принятия или отклонения нулевой гипотезы, которая утверждает, что данные распределены нормально. В справке XLSTATуказывается, что чем больше значение статистики, тем менее вероятна нулевая гипотеза, и следовательно, она должна быть отвергнута.

Три остальных теста (Бокса-Пирса, Льюнга-Бокса и МакЛеода-Ли) проверяют случайность данных (т. е. нулевая гипотеза утверждает, что данные принадлежат к белому шуму) и вычисляются для различных временных задержек. Все эти тесты используют распределение Хи-квадрат. Значение p-valueдля всех тестов соответствует вероятности ошибки при отвержении нулевой гипотезы или принятии, если она верна [4].

В таблице 1 записаны результаты применения тестов Харки-Бера, Бокса-Пирса, Льюнга-Бокса и МакЛеода-Ли к временным рядам. Согласно этим результатам наиболее вероятно что оба временных ряда представляют собой белый шум.

В рамках функции NormalityTestsк данным применяются нормальные тесты: Шапиро-Вилка (Shapiro-Wilk), Андерсона-Дарлинга (Anderson-Darling) andтест Лиллиефорса (Lilliefors), результаты которых тоже заставляют отклонить нулевую гипотезу и принять альтернативную.

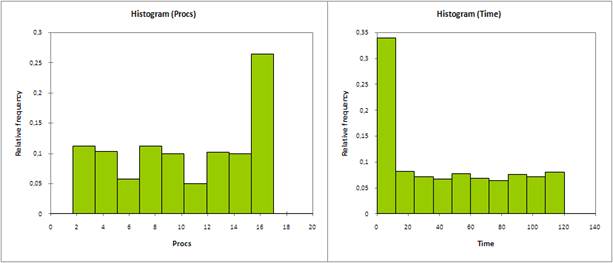
Наглядно ложность нулевой гипотезы о нормальности распределения значений во временных рядах Procsи Timeможно увидеть на гистограммах частот (рис. 1).

а                                                                                                                                б

Рис.1. Гистограммы частот распределения значений временных рядов Procs (а) и Time(б)

Как можно заметить, значения во всех промежутках распределены примерно равномерно кроме двух выступающих столбцов. Далее будет показано, что именно эти столбцы содержать циклические значения.

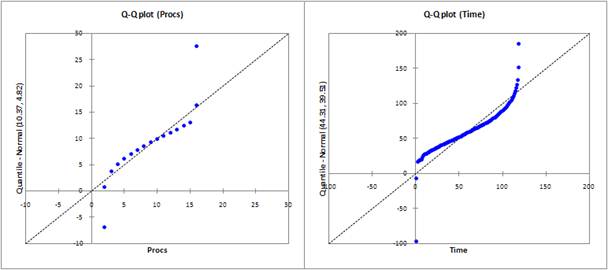
Помимо проведения тестов функция NormalityTestsпозволяет получить Q‑Qграфик, который сравнивает интегральную функцию распределения исследуемого временного ряда с интегральной функцией нормального распределения, имеющего ту же медиану и стандартное отклонение. В случае если входной временной ряд подчиняется нормальному распределению, график будет выровнен относительно первой биссектрисы [5].

а                                                                                                             б

Рис.2. Q‑Q графики, построенныедлявременныхрядовProcs (а) иTime(б)

На рисунке 2 изображены Q‑Qграфики для обоих временных рядов, из которых следует, что временные ряды не подчиняются нормальному закону, причем наибольшее отклонение от биссектрисы достигается, как и в случае с гистограммами, для значений, входящих в циклы.

Как результат всего вышеперечисленного, нулевая гипотеза, утверждающая, что данные распределены нормально, должна быть отвергнута. Вместе с тем, альтернативная гипотеза, что данные представляют собой белый шум, также должна быть отклонена на основании того, что достоверно известно о наличии в исходном ряде повторяющихся задач, несмотря на то, что автокоррелограммы не выявляют никаких периодических структур (рис. 3). Этот феномен может быть объяснен тем фактом, что циклические последовательности скрыты шумом остальных задач вследствие случайного количества заданий, поступающих каждый день.

Рис.3. Автокоррелограммы временных рядов Procs(а) и Time(б)

3. Моделирование случайного процесса GMDHShell

Несмотря на то, что статистический анализ выявил сходство исследуемого процесса назначения заданий с белым шумом, была предпринята попытка спрогнозировать поведение этого процесса с помощью специального программного обеспечения, т. к. первоначальное применение стандартных методов, например, ARIMA, не дало ожидаемого результата – погрешность метода зачастую превышала максимальное значение выборки в несколько раз.

В качестве используемого программного обеспечения был выбран пакет GMDHShell, разработанный компанией GeosResearchGroupи использующий метод групповой обработки данных (groupmethodofdatahandling) для решения разнообразных задач, таких как регрессионный анализ, классификация и прогнозирование временных рядов [3]. Отличительной особенностью GMDHShellявляется то, что он позволяет задавать в качестве входных данных временные ряды любой размерности; в данном случае исходный временной ряд был использован без изменений: дата поступления задания в очередь, количество запрашиваемых процессоров и продолжительность выполнения задания; прогнозируемым значением было выбрано количество запрашиваемых процессоров.

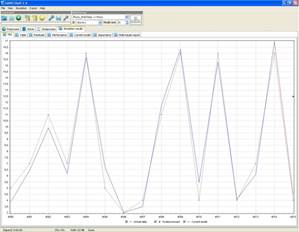
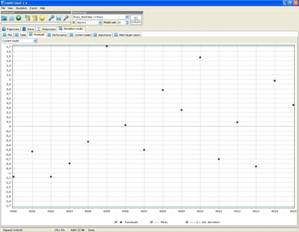
Несмотря на наличие мощного математического аппарата, результат использования данного программного продукта для моделирования процесса назначения работ достаточно неоднозначен: при использовании выборок сравнительно небольшого размера GMDHShellпозволяет получать модели с погрешностью, не превышающей 10 % от максимального значения (рис. 4), однако, эти модели не способны учитывать циклические составляющие, т.к. их период может быть сопоставим с размером выборки. Таким образом, возникает необходимость в увеличении размера входных данных, но одновременно с их увеличением растет и погрешность, и для обучающей выборки порядка 4000 элементов может достигать 100 % (рис. 5), тем самым делая невозможным использование данного продукта в полной мере.

а                                                                                                                      б

Рис.4. Модель (а) и погрешности (б) для выборки из 100 элементов. Показаны последние 15 элементов

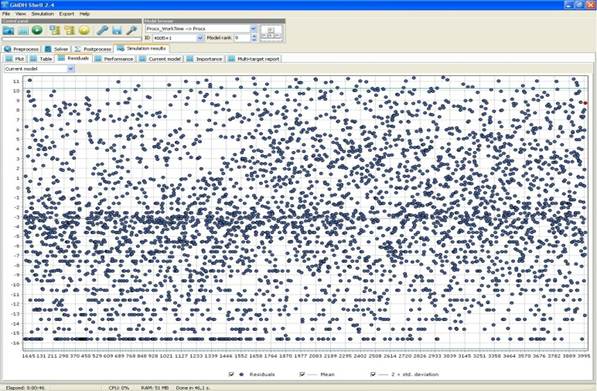
Рис. 5. Погрешность модели для выборки из 4000 элементов

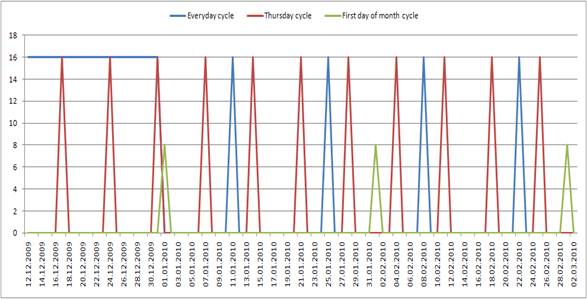
Как уже говорилось ранее, такое поведение можно объяснить слишком большим количеством «шума» – данных, которые снижают влияние циклов на общую выборку. Тем не менее, учитывая, что ни один из подходов не дал требуемого результата, и, основываясь на том, что мы наверняка знаем о наличии периодических компонентов в исходном временном ряду, было предложено явно выявить все существующие периодики. Применение такого подхода помогло обнаружить 3 продолжительных цикла: задачи, ставившиеся в очередь в первый день каждого месяца, задачи в течение ограниченного времени запускавшиеся каждый четверг и задачи, чья периодичность сначала составляла одни сутки, а потом увеличилась до двух недель (рис. 6).

Рис.6. Периодические компоненты, обнаруженные в процесс назначения работ (а) и в разрезе одного дня (б)

Теперь, обладая точными знаниями о существующих циклах, а также используя одну из моделей, сгенерированных GMDHShellдля небольшой выборки, удалось построить прогнозную модель с низкой погрешностью и одновременно с этим учитывающую циклические составляющие всего временного ряда (рис. 7). Для большей достоверности в этой модели был использован специальный коэффициент надежности, определяющий вероятность того, что в следующий временной шаг определенный цикл все еще будет существовать и зависящий от средней продолжительности остальных циклов.

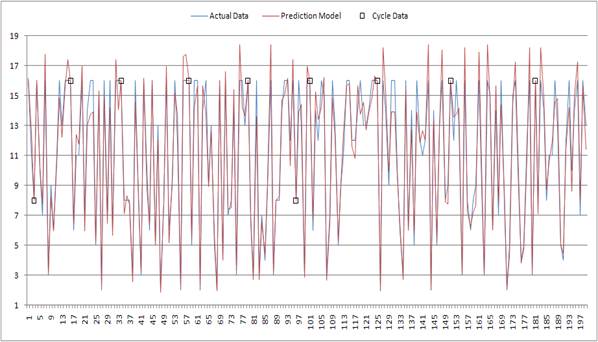
Рис. 7. Прогнозная модель, использующая данные о циклах

4. Заключение

Несмотря на получение достаточно точной модели процесса добавления заданий в очередь, очевидно, что данный подход должен использоваться только как дополнение к традиционным методам распределения ресурсов и планирования заданий, но не как самостоятельный алгоритм для систем управления распределенными ресурсами.

Более того, предстоит еще провести ряд дополнительных исследований, во-первых, с целью выявления наиболее подходящего метода расчета коэффициента надежности, а также чтобы обеспечить возможность обучения модели и изменения параметров в зависимости от входных данных.

Список литературы:

1. Гриценко Ан. В., Шульгин А. О. Исследование проблемы использования методов прогнозирования в алгоритмах управления заданиями и распределения ресурсов кластерных вычислительных систем. // В мире научных открытий. Выпуск № 8(20). Серия «Математика. Механика. Информатика». Красноярск: Издательство «Научно-инновационный центр», 2011. – С. 43—55
2. Интернет портал Gridтехнологий. Кластерные системы [Электронный ресурс]. URL: http://www.gridclub.ru/software/cluster.html (дата обращения 28.01.2012).
3. GMDH Shell. ProductOverview. Concepts [Электронныйресурс]. URL: http://www.gmdhshell.com/docs/concepts(датаобращения10.03.2012).
4. Statistics package for Excel – XLSTAT. Description and transformation of a time series with XLSTAT-Time [Электронный ресурс]. URL: http://www.xlstat.com/en/learning-center/tutorials/using-differencing-to-obtain-a-stationary-time-series.html (дата обращения 20.02.2012).
5. Statistics package for Excel – XLSTAT. Sampling and Normality test. [Электронный ресурс]. URL: http://www.xlstat.com/en/learning-center/tutorials/sampling-data-in-a-distribution-and-running-a-normality-test-with-xlstat.html (дата обращения 20.02.2012).