Статья опубликована в рамках: VIII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 19 марта 2012 г.)
Наука: Технические науки
Секция: Машиностроение и машиноведение
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
АППРОКСИМАТИВНАЯ МОДЕЛЬ ПРОГНОЗИРОВАНИЯ ОЦЕНОК РЕСУРСА
Подвойский Александр Олегович
ассистент кафедры «Техническая механикаи детали машин» СГТУ им. Гагарина Ю. А., г. Саратов
E-mail: apodvoyskiy08@gmail.com
Боровских Валентин Ефимович
д-р техн. наук, профессор кафедры «Техническая механикаи детали машин» СГТУ им. Гагарина Ю. А., г. Саратов
Теория прогнозирования оценок усталостной долговечности сложных механических систем насчитывает десятки различных моделей, методов и подходов, однако задача прогнозирования ресурса технических объектов (к которым относят несущие системы транспортных машин, силовые элементы двигателей и т. д.), функционирующих в условиях эксплуатационного нагружения, по-прежнему остается одной из не решенных задач прикладной механики. Следуя работе [1], заметим, что развитие аппроксимативных моделей прогнозирования, адаптированных к инженерным расчетам, является актуальным направлением динамики и прочности механических систем.
В работе [2] была предложена феноменологическая модель исчерпания прочностных характеристик объекта, основанная на гипотезе об исчерпании предела выносливости материала 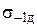 и кинетическом уравнении континуальной механики повреждаемости сплошных сред
и кинетическом уравнении континуальной механики повреждаемости сплошных сред
|
|
|
|
|
(1) |
где 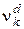 - текущая скалярная мера усталостных повреждений;
- текущая скалярная мера усталостных повреждений;  - текущее значение предела выносливости материала, МПа;
- текущее значение предела выносливости материала, МПа; 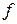 - эффективная частота процесса, Гц;
- эффективная частота процесса, Гц;  - коэффициент в корреляционной зависимости между пределом выносливости и пределом прочности по Эйхингеру;
- коэффициент в корреляционной зависимости между пределом выносливости и пределом прочности по Эйхингеру; 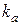 - коэффициент порога чувствительности;
- коэффициент порога чувствительности; 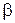 - коэффициент пропорциональности;
- коэффициент пропорциональности; 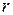 ,
, ,
,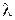 - материальные параметры модели,
- материальные параметры модели, 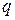 - число ступеней на траектории деградационного процесса;
- число ступеней на траектории деградационного процесса; 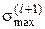 - максимальное значение процесса нагружения
- максимальное значение процесса нагружения 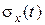 на отрезке
на отрезке 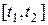 ;
;  - точки пересечения реализации процесса нагружения
- точки пересечения реализации процесса нагружения 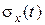 с текущим пределом выносливости
с текущим пределом выносливости  .
.
Как показал сравнительный анализ прогностических оценок ресурса найденных по модели (1) и по модели Полякова-Болотина [3], для различных комбинаций параметров автокорреляционной функции и кривой выносливости Велера наибольшее отклонение для модели (1) не превосходит 13 %; однако использование прогностической модели (1) в форме рекуррентного соотношения встречает некоторые сложности вычислительного характера, по этой причине представляется разумным разработать более простую и удобную для расчета модель.
Используя упрощенную методику идентификации материальных параметров (и полагая 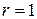 ,
, 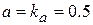 ), перепишем модель (1) для приращения ординаты деградационного процесса
), перепишем модель (1) для приращения ординаты деградационного процесса 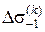 [
[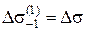 ] в виде
] в виде
|
|
(2) |
где 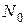 - абсцисса точки перегиба кривой усталости;
- абсцисса точки перегиба кривой усталости; 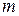 - показатель угла наклона левой ветви кривой усталости.
- показатель угла наклона левой ветви кривой усталости.
Выразив 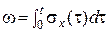 в соотношении (2) через интеграл Дирихле
в соотношении (2) через интеграл Дирихле 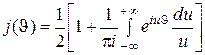 , получим выражение для средней площади
, получим выражение для средней площади 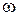 стационарного гауссовского процесса
стационарного гауссовского процесса
|
(3) |
где  - дисперсия процесса;
- дисперсия процесса; 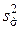 - дисперсия первой производной процесса;
- дисперсия первой производной процесса; 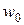 - круговая частота процесса по нулям,
- круговая частота процесса по нулям, 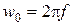 .
.
Подставив (3) в (2), получим 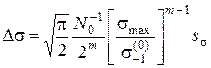 . Теперь определим число циклов до разрушения
. Теперь определим число циклов до разрушения  .
.
И, наконец, выразив  через среднеквадратическое отклонение
через среднеквадратическое отклонение  и разделив последнее соотношение на эффективную частоту процесса
и разделив последнее соотношение на эффективную частоту процесса 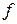 , получим формулу для расчета усталостной долговечности
, получим формулу для расчета усталостной долговечности
|
. |
(4) |
Модель (4) содержит ряд упрощений и потому нуждается в коррекции: как показал статистический анализ результатов вероятностного моделирования, в первой итерации соотношение (4) можно переписать в виде
|
|
(5) |
где 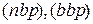 - условное обозначение соответственно узкополосного и широкополосного процесса.
- условное обозначение соответственно узкополосного и широкополосного процесса.
Теперь рассмотрим альтернативные модели и проведем сравнительный анализ оценок усталостной долговечности 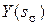 .
.
В работе D. Benasciuttiи R. Tovo[4] рассматривается ряд моделей для расчета оценок ресурса (в моделях реализован метод потоков дождя «RFC»):
- модель Narrow-bandapproximation: при нагружении широкополосными процессами оценка ресурса оказывается консервативной
|
|
(6) |
где 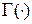 - гамма-функция.
- гамма-функция.
- модель T. Dirlik[5]: не имеет теоретической основы и в силу особенностей математической оболочки модели делает невозможным переход к негауссовским процессам [4]
|
|
(7) |
где 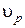 - частота процесса по экстремумам;
- частота процесса по экстремумам; 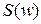 - спектральная плотность процесса;
- спектральная плотность процесса; 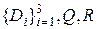 - параметры оптимальной подгонки.
- параметры оптимальной подгонки.
- модель W. Zhaoи M. J. Baker [6]: как показывают исследования [4], оценка Zhao-Bakerне может быть применена к процессам с параметром широкополосности
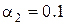
|
|
(8) |
где  - весовой коэффициент, (
- весовой коэффициент, (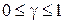 );
); 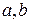 - параметры закона Вейбулла.
- параметры закона Вейбулла.
В работе [3] Б. Н. Поляков предлагает расчетно-экспериментальный подход к построению оценки усталостной долговечности (сформированный на основе корректного применения математических методов теории случайных величин и теории выбросов), учитывающий особенности статистических характеристик случайной кривой усталости и нагруженности в форме автокорреляционной функции, что позволяет отказаться от различных методов схематизации
|
|
(9) |
где 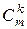 - число сочетаний;
- число сочетаний;  - математическое ожидание процесса;
- математическое ожидание процесса; 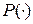 - функция Пирсона.
- функция Пирсона.
На рис.1 изображены кривые усталости по моделям (1), (5)—(9) для
случая нагружения стационарными гауссовскими стохастическими процессами с автокорреляционной функцией (АКФ) экспоненциально-косинусного типа 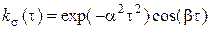 .
.
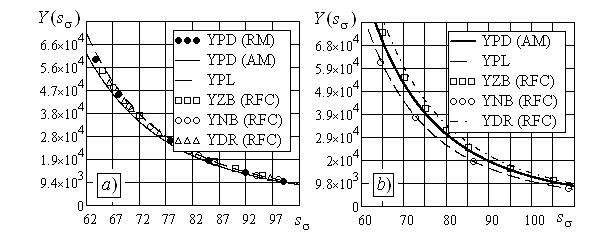
Рис. 1. Кривые усталости a) узкополосный процесс, b) широкополосный процесс
Параметры АКФ и кривой усталости для моногармонического нагружения:
- рис.1, а)
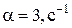 ;
;  ;
; 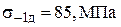 ;
;  ;
; 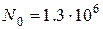 ;
; - рис.1, b)
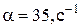 ;
; 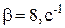 ;
; 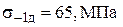 ;
;  ;
; 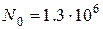 .
.
Таким образом, как это видно из рис.1 расчетные оценки ресурса найденные с помощью аппроксимативной модели (5), с достаточной для инженерной практики точностью близки к оценкам, вычисленным по хорошо известным апробированным моделям.
Модель (5), также как и рассмотренные модели корректно учитывает влияние прочностных характеристик объекта и спектрального состава стохастического процесса нагружения, однако в отличие от моделей (7)—(9) удобнее в использовании и не требует сложных вычислений.
Необходимо подчеркнуть, что аппроксимативная модель (5) представляет собой лишь одно из приближений общей модели (1) для случая нагружения стационарными гауссовскими процессами, и только указывает на то обстоятельство, что общая рекуррентная модель (1) в частном случае (стационарные процессы) дает оценки, согласующиеся с оценками, найденными с использованием общепринятых моделей.
Вообще же модель (1) позволяет оперировать достаточно широким классом стохастических процессов нагружения, включающим нестационарные, негауссовские и другие процессы.
Список литературы:
- Багмутов В. П. Прогнозирование надежности и долговечности углеродистых сталей при статистическом моделировании случайного внешнего нагружения / В. П. Багмутов, А. Н. Савкин// Известия Волгоградского государственного технического университета. - 2007. - № 1(27). - Вып. 1. - С. 12—17.
- Подвойский А. О. Прогнозирование оценки ресурса технического объекта по критерию текущего значения предела выносливости /А. О. Подвойский, В. Е. Боровских // Вестник Саратовского государственного технического университета. - 2011. - № 1(52). - Вып. 1. - С. 84—88.
- Поляков Б. Н. Методика оценки срока службы деталей с использованием теорий случайных величин и случайных процессов и ее применение / Б. Н. Поляков // Вестник машиностроения. - 2007. - № 2. - С. 28—34.
- Benasciutti D. Comparison of spectral methods for fatigue analysis of broad-band Gaussian random processes / D. Benasciutti, R. Tovo // Probabilistic Engineering Mechanics. - 2006. - № 21. - P. 287—299.
- Dirlik T. Application of computers in fatigue analysis: Thesis (Ph.D.); University of Warwick, Dept. of Engineering (UK). - Warwick, 1985 – 241 p.
- Zhao W. On the probability density function of rainflow stress range for stationary Gaussian processes / W. Zhao, M. J. Baker // International Journal of Fatigue. - 1992. - № 14(2). - P. 121—135.
дипломов


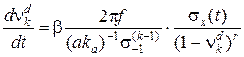 ,
, 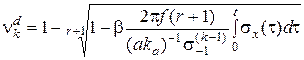 .
.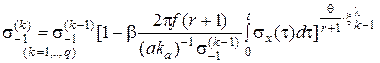 или
или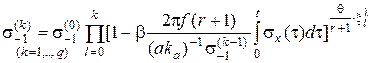 ,
,  ,
,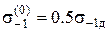 ,
,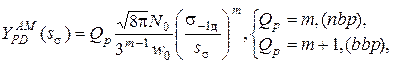
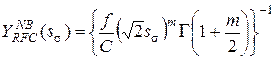 ,
, 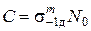 ,
,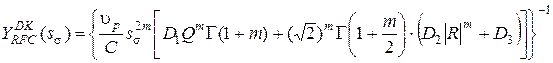 ,
, ,
, 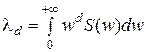 ,
, 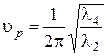 ,
, 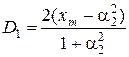 ,
, 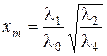 ,
, 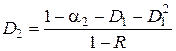 ,
,  ,
,  ,
, 
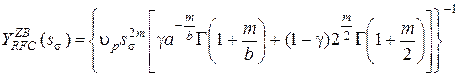 ,
, ,
,  ,
, 
 ,
, ,
,
Оставить комментарий