ОПРЕДЕЛЕНИЕ ИНДУКТИВНЫХ СОПРОТИВЛЕНИЙ НИЗКОСКОРОСТНОГО ТОРЦЕВОГО СИНХРОННОГО ГЕНЕРАТОРА

Архипцев Максим Геннадьевич

ассистент Пи СФУ, г. Красноярск

E-mail: maximus_09@mail.ru

Встовский Алексей Львович

канд. техн. наук, профессор Пи СФУ, г. Красноярск

E-mail: val_1942@mail.ru

Федий Константин Сергеевич

канд. техн. наук, доцент Пи СФУ, г. Красноярск

E-mail: Fediy_k@mail.ru

В схеме любой гидро- и ветроэнергоустановки весьма важным компонентом является генератор. Основными требованиями, предъявляемыми к генератору, являются: управляемость, возможность его эксплуатации на открытом воздухе и в воде в течение длительного времени с высокой степенью надежности.

Низкоскоростные торцевые синхронные генераторы (НТСГ) с возбуждением от постоянных магнитов обеспечивают наилучшие массогабаритные и энергетические показатели при малом осевом размере. Особенно это заметно при увеличении числа пар полюсов до 10 и более. В этом случае оказывается возможным снижение массы электрической машины в 2 и более раз. Малый осевой габарит генератора с возбуждением от постоянных магнитов дает возможность обеспечить конструктивную совместимость их с рядом механизмов, компактность, удобство эксплуатации и сборки, с возможностью получения требуемых характеристик (напряжение 220/380 В, ток до 15 А) при низких частотах вращения (от 80 до  600 об/мин).

Конструкция низкоскоростного торцевого генератора вызывает необходимость размещения в его объеме постоянных магнитов многополюсного ротора, обмоточных структур статора при ограничении радиального габарита машины, обеспечении качества выходного напряжения, формировании достаточно жесткой внешней характеристики [3]. В тоже время, торцевая конструкция не позволяет воспользоваться известными расчетными моделями и методиками расчета цилиндрической электрической машины, что требует создания расчетной модели, учитывающей специфику структуры и конфигурации активной зоны машины и особенности ее геометрии.

Математическая модель, основанная на классических схемных решениях, не позволяет эффективно провести оптимизацию параметров, с целью уменьшения массы и габаритов генератора и повышения его энергетических показателей. Поэтому разработка математической модели торцевого генератора велась с применением основных уравнений классической электродинамики, описывающих распределение электромагнитного поля в активном объеме машины с учетом нелинейности характеристик ферромагнитных материалов. Разработанное математическое описание синхронной машины позволяет рассчитывать токи, напряжения, электромагнитный момент в установившихся режимах [1, с. 129].

В синхронных машинах, применяемых в автономных источниках электроснабжения, постоянно возникают разнообразные переходные процессы: при резких изменениях режима работы (наброс или сброс нагрузки), внезапных коротких замыканиях. Переходные процессы, возникающие в синхронной машине, могут оказать большое влияние на качество электроснабжения потребителя.

Разработка математической модели переходных процессов в синхронном генераторе необходима для определения токов короткого замыкания, оценки влияния этих процессов на работу системы автоматического управления, выбор ее схемного решения.

Одной из основных задач исследования переходных процессов является определение параметров, определяющих величины напряжений и токов в обмотках генераторов. Такими параметрами, прежде всего, являются индуктивные сопротивления обмоток генератора. Активными сопротивлениями в синхронных машинах большой и сверхбольшой мощности пренебрегают вследствие их малости, и лишь в машинах сравнительно малой мощности (до 50 —  100 кВт) их учитывают, поскольку их величина соизмерима с индуктивными сопротивлениями.

В настоящей работе для моделирования переходных процессов торцевого низкоскоростного синхронного генератора применены общепринятые подходы исследования переходных процессов в синхронных генераторах цилиндрической конструкции с электромагнитным возбуждением, с учетом особенностей магнитоэлектрического возбуждения исследуемого генератора [4, с. 25] и распределения магнитных потоков в торцевой конструкции.

В рассматриваемой модели генератора, постоянный магнит полюса заменен эквивалентной одновитковой обмоткой, включенной на источник тока , равным МДС фиктивной коэрцитивной силы . Полюсные наконечники представляют стержнями демпферной обмотки, также подключенными к источнику тока. Такая замена позволяет представить уравнения равновесия напряжений синхронного генератора с постоянными магнитами по аналогии с уравнениями обычной синхронной машины.

Обмотки статора и ротора имеют в общем случае разные число фаз и число витков, различное распространение в пространстве, поэтому необходимо произвести приведение роторной обмотки к статорной, через коэффициенты приведения. Основным условием приведения является постоянство полной мощности в реальных и приведенных обмотках.

Для каждой из обмоток машины можно записать уравнения второго закона Кирхгофа [4, с. 28]:

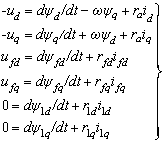                                                             (1)

С учетом явнополюсности, входящие в (1) потокосцепления связаны друг с другом соотношениями:

                                                            (2)

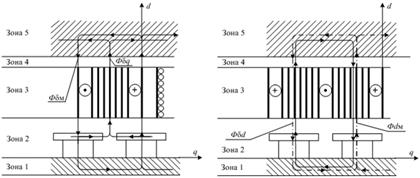
Дифференциальные уравнения (1), (2), устанавливают связь между напряжениями, токами и потокосцеплением машины. В них в качестве коэффициентов входят активные сопротивления обмоток якоря, возбуждения и демпферной, индуктивности само- и взаимоиндукции обмоток. Эти электрические параметры необходимы и для определения точки отхода прямой возврата и ЭДС холостого хода и зависят от формы магнитного поля в рабочем зазоре и, следовательно, от конструкции ротора. На рисунках 1—4 представлена расчетная модель явнополюсного низкоскоростного торцевого синхронного генератора с постоянными магнитами, с помощью которой можно составить схемы замещения магнитной цепи [2, с. 178], и определить магнитные проводимости для составляющих магнитного потока машины и далее все выше перечисленные электрические параметры.

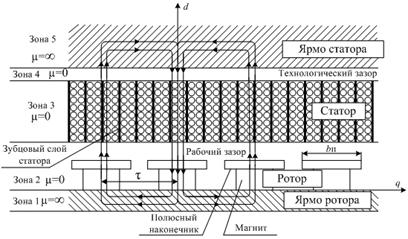
Рисунок 1. Расчетная модель явнополюсного генератора

Распределение МДС и магнитных потоков при различных положениях ротора, характеризующее распределение полей ротора и статора, представлено на рисунках 2, 3, 4

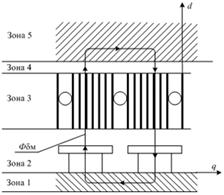
Рисунок 4. Распределение магнитного поля постоянного магнита

На основании представленных расчетных моделей составлены схемы замещения магнитных цепей для различных положений ротора, показанные на рисунке 5.

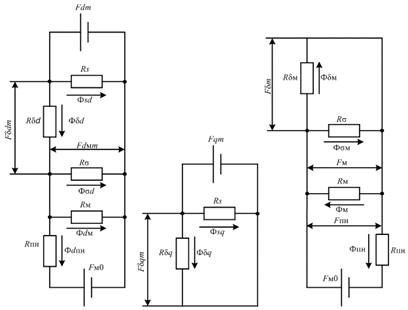
Рисунок 5. Схемы замещения магнитных цепей.

Сопротивление воздушного зазора  для потока  будет равно:

.                                   (3)

Аналогично находят сопротивление  для потока :

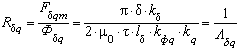.                                  (4)

Сопротивление рабочего зазора  для потока  будет равно:

.                                  (5)

Сопротивление полюса магнита по продольной оси:

.                                                         (6)

Сопротивление рассеяния якоря:

.                                                          (7)

Сопротивление рассеяния ротора на один полюс:

.                                                                                               (8)

Коэффициенты формы поля, входящие в формулы магнитных сопротивлений, определяются разложением в гармонический ряд индукций соответствующих полей. Так как в синхронных машинах с постоянными магнитами воздушный зазор равномерен и невелик, а длина полюсной дуги значительна, то можно принять, что поле в рабочем зазоре в пределах полюсной дуги для ротора распределено по прямоугольному закону, для статора — по синусоидальному закону, а в промежутках между полюсами равно нулю.

На рисунках 6 показаны магнитные поля реакции якоря по продольной оси и обмотки возбуждения явнополюсной синхронной машины.

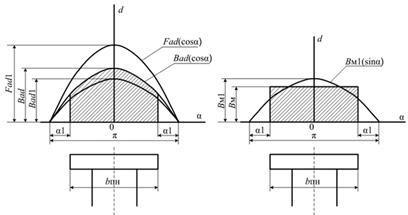
Рисунок 6. Распределение магнитных полей реакции якоря по продольной оси и постоянных магнитов явнополюсной синхронной машины.

Для определения коэффициента формы поля продольной реакции якоря , который определяет уменьшение амплитуды основной волны поля по сравнению с её значением при равномерном воздушном зазоре, необходимо найти основную гармоническую поля.

Определим первую гармонику индукции в зазоре, исходя из рисунка 6:

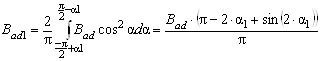.       (9)

Коэффициент

.                                     (10)

Так как зазор под наконечником полюса является равномерным и весьма малым, то поле возбуждения имеет вид прямоугольной кривой, основание которой равно b_пн. Эта кривая имеет основную гармоническую, амплитуда которой

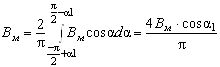.                                         (11)

Коэффициент формы поля возбуждения определяется как отношение амплитуды индукции основной волны поля возбуждения , к максимальному значению индукции этого поля

.                                                                  (12)

Коэффициент продольной реакции равен:

.                                       (13)

На рисунке 7 показано магнитное поле реакции якоря по поперечной оси. Величина индукции этого поля определяется следующим образом:

.  (14)

Тогда коэффициент формы поля поперечной реакции будет равен:

 .  (15)

Рисунок 7. Распределение магнитного поля реакции якоря по поперечной оси.

Коэффициент поперечной реакции равен:

.                                                                  (16)

Значения коэффициентов формы поля, полученные по формулам (10), (12), (13), (15), (16), с учетом разложения в гармонические ряды:

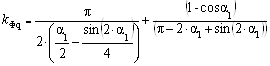
Магнитные проводимости получены как обратная величина соответствующих сопротивлений в схемах замещения (рис. 5), с учетом значений коэффициентов формы соответствующих магнитных полей.

Определив все коэффициенты формы поля, можно определить индуктивные сопротивления. Главное индуктивное сопротивление якоря по продольной оси машины будет равно:

                                                           (17)

где 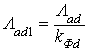 – магнитная проводимость воздушного зазора по продольной оси; .

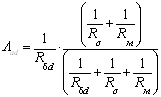Главное индуктивное сопротивление якоря по поперечной оси машины:

                                                           (18)

где  — магнитная проводимость воздушного зазора по поперечной оси; .

Полные индуктивные сопротивления якоря:

                                                                                 (19)

                                                                                   (20)

где  — индуктивное сопротивление рассеяния.

После определения всех параметров можно, применяя операторный метод, вывести уравнения токов для трехфазного короткого замыкания [4, с. 88] низкоскоростного торцевого генератора, а также применить эти параметры для определения его выходных характеристик.

Список литературы:

1.        Встовский А. Л. Анализ магнитного поля торцевого синхронного генератора с магнитоэлектрическим возбуждением / IV Международная научно-практическая конференция «Электромеханические преобразователи энергии», сб. трудов. — Томск, 2009 — С. 127—136.

2.        Осин, И. Л., Электрические машины. Синхронные машины. М.: Высш. шк., 1990. — 304 с.

3.        Патент 2246168 Российская Федерация, МПК⁷ Н 02 К 21/24 / Торцевая электрическая машина / А. Л. Встовский, М. П. Головин и др.; заявитель и патентообладатель Краснояр. гос. техн. ун-т. — № 2003123588/09; заявл. 24.07.03; опубл. 10.02.05, Бюл. № 2.— 6 с.: ил.

4.        Сипайлов, Г. А., Электрические машины (специальный курс). М.: Высш. шк., 1987. — 287 с.