МОДЕЛИРОВАНИЕ ПРОЦЕССА ИСПАРЕНИЯ УГЛЕВОДОРОДОВ НЕФТИ ПРИ НАПОЛНЕНИИ РЕЗЕРВУАРА

Базил Гульмира Дуйсенбеккызы

преподаватель КазНТУ им. К. И. Сатпаева, г. Алматы

Е-mail: bazilg@bk.ru

При хранении легкоиспаряющихся жидкостей в резервуарах различают два основных вида потерь — это потери от так называемых «малых дыханий» и «больших дыханий». Кроме того, имеются потери от «обратного выдоха», и от вентиляции газового пространства резервуаров.

Потери от испарения происходят главным образом при хранении в резервуарах нефти и легкоиспаряющихся нефтепродуктов, представляющих собой сложные смеси весьма большого числа индивидуальных углеводородных компонентов. [1, с. 175].

Динамику испарения углеводородов с открытой поверхности нефти в резервуаре можно описать в виде численной модели процесса испарения при «больших дыханиях» во время наполнения резервуара. [2, с. 15].

Скорость испарения углеводородов равна разности скорости перехода молекул из жидкости в газ , и скорости конденсации  (переход молекул из газа в жидкость) паров:

                                                                            (1)

В течение некоторого промежутка времени скорость конденсации пара будет пропорциональна его плотности  и, следовательно, с учетом скорости насыщения пара, уместно ввести определяемый опытным путем коэффициент скорости k:

                                                                                       (2)

За некоторый промежуток времени плотность паров углеводородов под крышей резервуара станет достигать предельного значения насыщенности, пропорциональной скорости испарения:

                                                                                   (3)

Массу испарившихся паров углеводородов с поверхности нефти S можно представить следующей формулой:

                                                                       (4)

Откуда плотность  выражается как

                                                                                                    (5)

Так как плотность паров углеводородов изменяется во времени, продифференцируем обе части уравнения:

                                                                                               (6)

В правую часть подставим значение массы из формулы (4), и, решая уравнение (6), получим значение плотности паров углеводов (7), изменяющееся во времени:

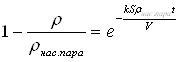
                                              (7)

Формула (7) представляет собой экспоненциальную зависимость плотности паров углеводородов от времени.

Численное моделирование процесса наполнения нефтяного резервуара проиллюстрируем на примере вертикального стального резервуара без понтона (РВС-20000) резервуарного парка нефтеперекачивающей станции, объемом 20000 м³ и площадью поверхности испарения 1698 м², скоростью наполнения и опорожнения нефтью 4000 м³/ч. Плотность насыщенных паров примем равной 300 г/м³. Предположим что время полного насыщения, т. е. до 99 % парами углеводородов газовоздушного пространства над поверхностью нефти в резервуаре равно 1 часу.

Теоретически вычисляется коэффициент скорости k.

Для времени t=1 час по формуле (7):

Далее для сравнительного анализа процесса испарения при различных времен хранения аналогичным способом рассчитываем коэффициенты скорости времени насыщения парами углеводородов за 2, 4, 8 и 24 часа:

Таблица 1

Коэффициенты скорости для различных времен

Принимая вышеизложенное можно рассчитать изменение плотности паров углеводородов над «зеркалом» за текущее время  и построить график экспоненциальной зависимости плотности насыщения от времени.

Таблица 2

Зависимость плотности насыщения паров углеводородов от времени

По полученным расчетным данным достаточно четко прослеживается кинетика испарения углеводородов с поверхности нефти внутри резервуара: чем дольше нефть храниться в резервуаре, тем больший объем паров углеводородов испарится, это так же прослеживается на нижеприведенных графиках зависимости плотности насыщения паров от времени.

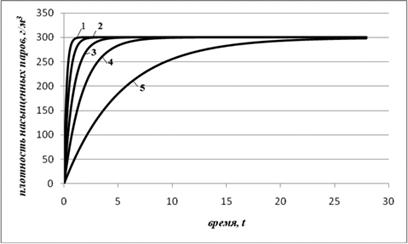
Рисунок 1. Зависимости плотности насыщения паров от времени при различных коэффициентах скорости k: 1 — при k=0,181; 2 — при k=0,091; 3 — при k=0,45; 4 — при k=0,23; 5 — при k=0,0075

Используя программный пакет Matlab, для нахождения передаточной функции по данным, приведенным в таблице 1, выполняем аппроксимацию и получаем кривую (рисунок 2).

Рисунок 2. Апроксимированная кривая зависимости плотности насыщения паров от времени

С помощью данной кривой находим передаточную функцию:

                                                                      (9)

В этой же программе, выполнив процедуру идентификации, находим коэффициенты пропорциональности и времени передаточной функции (рисунок 3).

Рисунок 3. Передаточная функция и значения коэффициентов

В итоге передаточная функция приобретает следующий вид:

Далее строим переходную (при ступенчатом воздействии) и амплитудно-фазовую характеристики (рисунок 4), где видно, что наша модель является устойчивой.

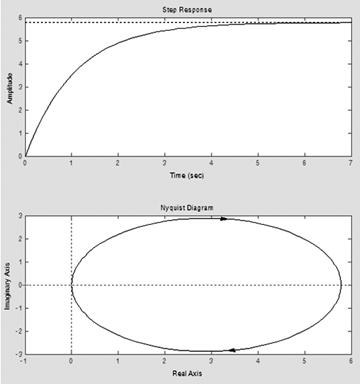
Рисунок 4. Переходная и АФ характеристики

Таким образом также можно получить модели испарения при опорожнении — «обратном выдохе», хранении — «малых дыханиях» и вентиляции. Далее, объединив все полученные модели в единую систему, можно получить общую картину потерь углеводородов нефти при эксплуатации резервуарного парка, что позволит рационально управлять работой резервуаров.

Список литературы:

1.        Бунчук В. А. Транспорт и хранение нефти, нефтепродуктов и газа: М., Недра, 1977. — 366 с.

2.        Васильев А. О. Чартий П. В. Моделирование и оптимизация работы нефтяных резервуаров, оснащенных средствами сокращения выбросов углеводородов. [электронный ресурс] — Режим доступа. — URL: http://bashexpert.ru/konkurs/2008/one/proekt13.pdf