КВАДРАТИЧНЫЕ ПОЛЯ ГАЛУА И ИХ ПРИМЕНЕНИЕ В СХЕМАХ ЦИФРОВОЙ ПОДПИСИ НА ОСНОВЕ КОНЦЕПЦИИ ПРОЛОНГИРОВАННОЙ БЕЗОПАСНОСТИ

Бондарь Виктория Витальевна

канд. физ.-мат. наук, доцент СГУ, г. Ставрополь

E-mail: viktori-bondar@yandex.ru

Одним из важнейших направлений развития современной криптографии являются системы пролонгированной безопасности. Системы данного типа базируются на совместном применении принципов пространственного разделения и периодического обновления секретной информации. Механизмы пролонгированной безопасности могут быть применены для модификации любого класса протоколов безопасности, используемых в распределенных вычислительных системах. К числу таких протоколов относятся протоколы аутентификации пользователей, управления криптографическими ключами, создания электронных цифровых подписей, коммуникационные протоколы и т. д.

Предложим модификацию протокола электронной цифровой подписи DSA из [2, с. 91—92] на основе математической модели пролонгированной безопасности с использованием квадратичных полей Галуа из [1, с. 36—38]. Допустим, что  абонентов, составляющих распределенную вычислительную сеть (РВС), должны поставить общую электронную цифровую подпись (ЭЦП) под некоторым сообщением М. Например, в качестве абонентов могут выступать  предприятий, образующих холдинг-компанию, а сообщение М может представлять собой некий документ, касающийся совместной деятельности предприятий. Очевидно, что в этом случае должен быть выработан механизм создания общей ЭЦП, гарантирующий, что ни одно из предприятий, входящих в холдинг, не сможет самостоятельно поставить подпись под документами такого рода.

Известно, что система ЭЦП включает в себя две процедуры: 1) процедуру постановки подписи и 2) процедуру проверки подписи. В процедуре постановки подписи используется секретный ключ отправителя сообщения, а в процедуре проверки подписи — открытый ключ отправителя.

В предлагаемой схеме для того чтобы выработать общую пару ключей (открытый и секретный ключи), доверенный центр абонентов сначала генерирует следующие параметры:

1.         р — большое простое число, удовлетворяющее условиям: р > n,

<р<, битовая длина р кратна 64;

2.         Q — большое простое число, удовлетворяющее условиям: битовая длина Q равна 160, (р — 1) Q;

3.         , где .

Параметры  не являются секретными и распространяются среди всех абонентов сети. Далее доверенный центр выбирает случайное целое число  и вычисляет значение . Число у является общим открытым ключом, используемым для проверки совместной подписи абонентов рассматриваемой РВС. Число х является общим секретным ключом абонентов для подписи совместных сообщений. Данное число сохраняется в секрете и с помощью -пороговой схемы разделения секрета (СРС) разделяется между абонентами сети.

Процесс разделения доверенным центром секретного ключа х включает в себя следующие этапы:

1.         Каждому i-му абоненту присваивается характеристическое число , где  >,  для любых  (,). Отметим, что секретный ключ х необходимо выбирать исходя из условия , где <, причем произведение любых (k — 1) чисел из  меньше , а произведение любых k чисел из  больше .

2.         Вычисляются «проекции» секретного ключа , отсылаемые абонентам сети:  .

Будем считать, что СРС функционирует в режиме пролонгированной безопасности, причем периодическое обновление «проекций» общего секретного ключа осуществляется с использованием «блуждающих» ключей. В качестве пространства «блуждающих» ключей выберем квадратичное поле Галуа

=,

где  — квадратичный невычет по модулю .

Абоненты сети заранее находят один из квадратичных невычетов а по модулю р и генерируют элементы поля , среди которых выбирают элемент , имеющий довольно большой порядок. Число q не является секретным. Кроме того, абоненты заранее договариваются о начальном ключе  и формируют последовательность случайных целых чисел  таких, что

1<<  (эта информация сохраняется в секрете).

Пусть в результате применения пороговой СРС каждый абонент  получил свою пару значений , где  — секретная «проекция» го абонента. Представим «проекцию» в виде многочлена , где =, и будем записывать «проекцию» секрета абонента  в виде вектора . Применение так называемого «вторичного» пространственного разделения секретной информации усложнит задачу вскрытия противником сервера абонента, так как координаты секретного вектора могут храниться на сервере отдельно.

Смена «проекций»  общего секретного ключа  осуществляется путем преобразований шифрования, аналогичных тем, которые применяются в криптосистеме Эль-Гамаля. Механизм смены секретных «проекций» абонентов РВС в рамках j-го сеанса связи можно представить в виде следующей последовательности действий:

.

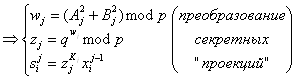
После  сеансов смены секретных «проекций» получим

.

Для того чтобы восстановить начальную секретную «проекцию» , абонент  должен выполнить следующую последовательность действий:

В результате общий ключ х может быть восстановлен по формуле

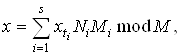
где  ,  и  — множество, определяющее структуру доступа в данной СРС.

Рассмотрим процедуру постановки совместной подписи. Допустим, что после l-го сеанса смены «блуждающих» ключей и соответствующей смены «проекций» общего секретного ключа абонентам сети потребуется поставить ЭЦП под некоторым сообщением М. Для того чтобы подписать сообщение М, абоненты РВС, входящие в структуру доступа, сначала хэшируют его с помощью хэш-функции  в целое число  (1<<), далее генерируют случайное целое число К (1<К<Q) и вычисляют число  по формуле

.

Затем данная группа абонентов с помощью секретного ключа  вычисляет целое число s по формуле . В результате под сообщением М ставится совместная цифровая подпись . Подчеркнем, что данную подпись могут поставить только абоненты, входящие в структуру доступа, т. к. в противном случае (если число абонентов меньше k) общий секретный ключ x не может быть восстановлен, а, следовательно, получение подписи S невозможно.

Тройка чисел  передается получателю сообщения по открытым каналам связи. При этом пара чисел (К,x) сохраняется в секрете.

Процедура проверки подписи заключается в том, что получатель сообщения  должен удостоверить в том, что подпись  соответствует сообщению М. Для этого получатель сначала проверяет выполнение условий и отвергает подпись, если хотя бы одно из этих условий не выполнено. Затем получатель вычисляет значение , хэш-значение  и числа , .

Далее получатель с помощью открытого ключа  вычисляет значение

и проверяет выполнение условия  Если это условие выполняется, то подпись  под документом М признается получателем подлинной.

Можно строго математически доказать, что последнее равенство будет выполняться тогда и только тогда, когда подпись  под документом М получена с помощью именно секретного ключа х, из которого был получен открытый ключ у. Таким образом, можно надежно удостовериться, что отправитель сообщения владеет именно данным секретным ключом х (не раскрывая при этом значения ключа х) и что отправитель подписал именно этот документ М.

Список литературы:

1.        Бондарь В. В., Семенова Н. Ф. Использование полей Галуа для разработки математической модели пролонгированной безопасности с «блуждающими» ключами // Инфокоммуникационные технологии. Т. 2, № 3, 2004. — С. 36—38.

2.        Черемушкин А. В. Криптографические протоколы. Основные свойства и уязвимости: учеб. пособие. М.: Издательский центр «Академия», 2009. — 272 с.