МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОПРЕДЕЛЕНИЯ РАСХОДА ОХЛАЖДАЮЩЕЙ ЖИДКОСТИ ДЛЯ КРИСТАЛЛИЗАТОРА В МАШИНЕ НЕПРЕРЫВНОГО ЛИТЬЯ ЗАГОТОВОКВ СРЕДЕ MATLAB

Воронин Станислав Сергеевич

студент 5 курса НФ НИТУ «МИСиС», г. Новотроицк

E-mail: voronsot@mail.ru

Давыдкин Максим Николаевич

канд. техн. наук, ст. преподавтель НФ НИТУ «МИСиС», г. Новотроицк

E-mail: kredopc@rambler.ru

Современное состояние теории непрерывной разливки стали позволяет определить основные технологические параметры расчетным путем. Одним из таких параметров является расчет количества охлаждающей жидкости для кристаллизатора в МНЛЗ.

Главной целью построения математической модели является определение технологических параметров для конкретного процесса затвердевания заготовки. Такая необходимость часто возникает не только во время проектирования новых МНЛЗ, но и для уже работающих агрегатов, с целью проведения экспериментальных исследований, оптимизации уже установившегося на машине процесса литья или возможности создания систем автоматического управления.

Основными факторами, влияющими на расчет количества охлаждающей жидкости, являются: скорость литья заготовки, геометрические параметры кристаллизатора, разность температур охлаждающей жидкости на входе и на выходе из кристаллизатора, разность температуры жидкого металла на входе и корочки металла на выходе из кристаллизатора.

Затвердевание слитка в кристаллизаторе во многом определяет его качество. Методика расчета скорости затвердевания заготовки, основанная на решении задачи Стефана [2], заложена в математической модели. Она описывает затвердевание полуограниченного массива, предполагая отсутствие двухфазной зоны, гладкий фронт кристаллизации, отсутствие перегрева над температурой кристаллизации и наличие граничных условий теплообмена первого рода. Первое приближение аналитического решения задачи Стефана для скорости затвердевания представляет параболу:

,                                             (1)

где  – толщина корочки, мм;

– коэффициент затвердевания;

 – продолжительность затвердевания, мин;

h – расстояние до середины кристаллизатора, м;

– рабочая скорость вытягивания заготовки, м/мин.

Формула (1) используется для оценки толщины корки и скорости затвердевания расплава. Величину  достаточно сложно рассчитать теоретически для конкретных случаев. Поэтому на практике чаще пользуются значениями этого коэффициента, полученными экспериментальным путем. Для слябовых заготовок из углеродистых сталей средняя величина  находится в пределах 0,003…0,0036 м^-0,5с (23…28 мм мин^-0,5).

Расчет выполняется с учетом диаметра каналов, их количества и соблюдением следующих условий:

-     температура воды на выходе из кристаллизатора не должна превышать 40…45 ⁰С с тем, чтобы не происходило отложение растворенных в ней солей;

-     скорость движения воды в каналах должна быть не менее 2 м/с для того, чтобы предотвратить возникновение локальных перегревов.

Расход охлаждающей жидкости, обеспечивающий принятую температуру ее на выходе из кристаллизатора, можно определить по следующей формуле [5]:

                                                           (2)

где – расход воды на кристаллизатор по рассматриваемому условию, м³/ч;

 – средний тепловой поток, Вт/м²;

– площадь поверхности кристаллизатора, воспринимающая тепловой поток, м²;

 – плотность воды, кг/м³;

 – удельная теплоемкость воды, кДж/(кг∙град);

– разность температур охлаждающей жидкости на входе и выходе из кристаллизатора.

Расход охлаждающей жидкости, обеспечивающий скорость ее движения в каналах кристаллизатора, определяется по формуле [5]:

                                              (3)

где – расход воды на кристаллизатор, м³/ч;

 – диаметр канала, м;

 – скорость движения воды, м/с;

 – количество каналов.

Математическая модель вычисляет рабочую, минимальную и максимальную скорость вытягивания заготовки, площадь поверхности кристаллизатора и необходимое количество каналов для охлаждающей жидкости.

Модель реализована в среде MATLAB в виде отдельных блоков, каждый из которых имеет входные и выходные переменные и выполняет расчет отдельного параметра или функции (рис. 1). В модели представлены следующие блоки: скорость вытягивания заготовки, площадь поверхности кристаллизатора, средний слой затвердевшего металла в кристаллизаторе, тепловой поток, количество каналов для охлаждения, расчет расхода охлаждающей жидкости.

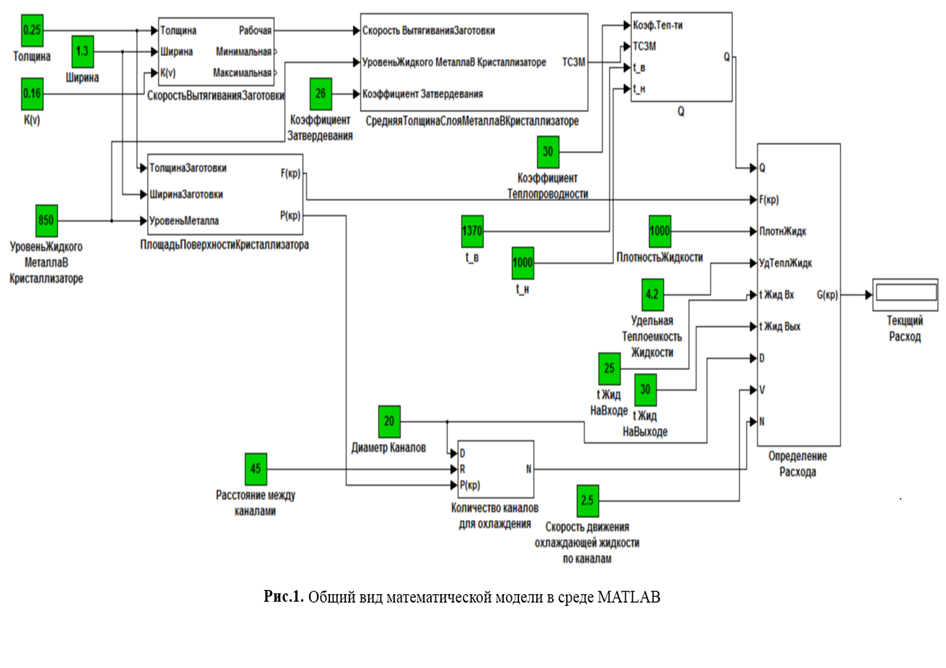
В качестве примера рассмотрим влияние разности температур охлаждающей жидкости на входе и на выходе из кристаллизатора на ее расход.

Пусть для охлаждения непрерывнолитой заготовки шириной 1,3 м и толщиной 0,25 м на входе в кристаллизатор подается вода с холодильной установки с температурой . Величину температуры воды на выходе будем изменять от 30 до 35 ^оС. Выполнив расчет на модели, получили зависимость, представленную на рисунке 2.

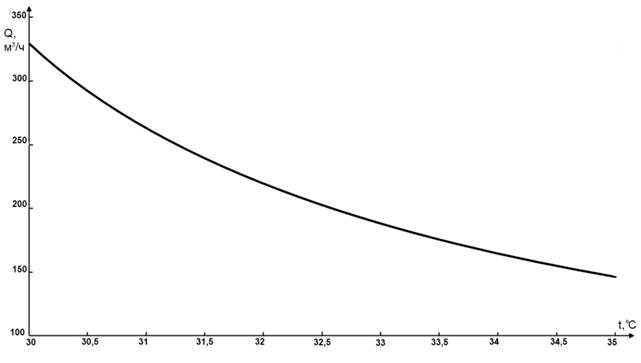
Рисунок 2. Зависимость расхода воды от ее температуры на выходе при постоянной температуре на входе

Анализируя полученную зависимость, можно сделать следующий вывод: чем больше разность между температурой воды на входе и на выходе кристаллизатора, тем меньше необходимо жидкости для охлаждения кристаллизатора. Это объясняется следующим: чем меньше нагревается вода при проходе по каналам кристаллизатора, тем меньше она забирает тепла со стенок кристаллизатора (либо у находящегося внутри жидкого металла). Следовательно, чтобы обеспечить постоянную температуру металла на выходе и одинаковую толщину корочки необходимо расходовать большее количество воды, и наоборот.

На основании проведенных исследований было доказано, что математическая модель может быть использована для расчета расхода охлаждающей жидкости в кристаллизаторе. С помощью модели возможно построение зависимостей расхода жидкости от скорости непрерывной разливки стали, толщины и ширины заготовки, параметров настройки кристаллизатора. С помощью коэффициентов можно изменять марку выплавляемой стали, что является одним из самых важных критериев в современном металлургическом производстве.

Список литературы:

1.            Бровман М. Я. Непрерывная разливка металлов: Научное издание. М.: «Экомет», 2007.-484 с.

2.            Буланов Л. В. Машины непрерывного литья заготовок. Теория и расчет. Екатеринбург: Уральский центр ПР и рекламы – «Марат», 2003.-320 с.

3.            Дюдкин Д. А. Современная технология производства стали. М.: Теплотехник, 2007.-528 с.

4.            Нисковских В. М. Машины непрерывного литья слябовых заготовок. М.: Металлургия, 1991.-279 с.

5.            Селиванов В. Н., Столяров А. М. Расчет технологических параметров непрерывной разливки стали: Методические указания. – Магнитогорск: МГМИ, 1993.-14 с.