К ВОПРОСУ СИНТЕЗА САР МНОЖЕСТВЕННЫХ ОБЪЕКТОВ УПРАВЛЕНИЯ

Марченко Юрий Николаевич

канд. тех .наук , начальник ИВЦ НФИ КемГУ, г. Новокузнецк

Трубецкой Вячеслав Сергеевич

зав. лабораторией разработки, внедрения и сопровождения программного обеспечения, НФИ КемГУ, г. Новокузнецк

Марченко Полина Юрьевна

рук. группы системного администрирования, НФИ КемГУ, г. Новокузнецк

E-mail:

Многочисленные процессы в живой природе, технических устройствах, и производственных системах по числу входов-выходов могут быть представлены следующими математическими моделями [2, с. 31]:

1)  модель с одним входом и одним выходом (рисунок 1а);

2)  модель с одним входом и несколькими выходами (рисунок 1б);

3)  модель с несколькими входами и одним выходом (рисунок 1в);

4)  модель с несколькими входами и несколькими выходами (рисунок 1г).

Рисунок 1. Структуры моделей

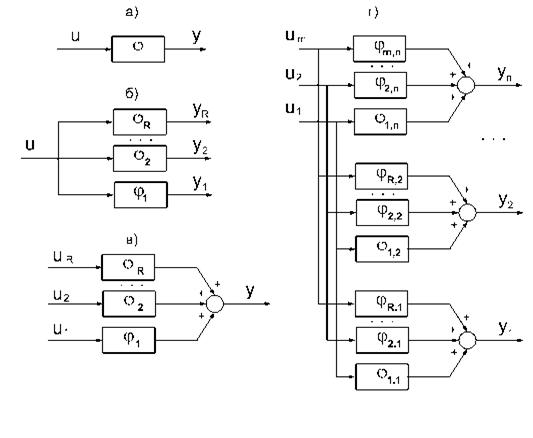
Во всех случаях сигналы от каждого входа к каждому выходу проходят по одному или нескольким параллельным каналам преобразования воздействий, имеющих различные запаздывания как в каналах управлениях, так и в состояниях объекта управления.

Модель на рисунке 1г может быть представлена комбинацией моделей представленных на рисунке 1б при  или комбинацией моделей представленных на рисунке 1в при .

Рисунок 2. Модель объекта

На рисунке 2 приведен вариант такого представления для объекта с тремя управляющими входами и двумя выходными целевыми переменными. В соответствии с тем, что  объект может быть, например, представлен комбинацией двух моделей:  и  (число моделей в общем случае определяется из условия min={m, n}).Отнесение управляющих воздействий к той или иной модели определяется значимостью управляющего воздействия по влиянию на выходную переменную. Наиболее значимое из группы управляющих воздействий будем называть основным. В качестве основных следует выделять каналы, оказывающие наиболее существенное влияние на соответствующую выходную переменную (например, имеющие минимальное запаздывание и (или) большой коэффициент передачи). Группу каналов управления -ой выходной переменной (-ый контур модели) составляют каналы, имеющие коэффициенты передачи на соответствующую выходную переменную больше чем на все остальные. Блоки  «отражают» взаимное влияние контуров модели. Полезность такого представления будет показана ниже при синтезе систем регулирования.

Необходимость таких моделей обусловлена особенностями конкретных технологических процессов – ограничениями на частоту и величину управляющего воздействия их соотношение и т. п.

Управляющие воздействия могут быть различны по физической природе – расход сыпучих материалов, расход газа, расход воды, пульпы, скорости перемещения рабочего органа или одного вида, например, компоненты шихтовой смеси.

Ниже объекты управления, описываемые моделями представленными на рисунках 1б и 1в будем называть множественными объектами управления соответственно первого и второго типа.

Синтез системы регулирования с объектами первого типа

Объекты управления, описываемые моделями первого типа, характеризуются совокупностью следующих основных признаков:

·     - число регулирующих воздействий меньше числа регулируемых выходных переменных;

·     - наличие неконтролируемых координатных возмущений;

·     - каналы регулирования имеют одинаковую физическую природу.

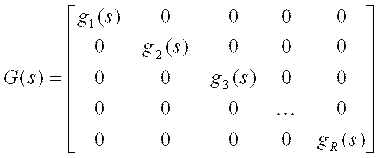
Общая структура объекта управления может быть задана в виде:

где -матричная передаточная функция

,

- вектор управляющих воздействий , -

матрица коэффициентов, определяющих распределение регулирующих воздействий по каналам регулирования  ,  - неконтролируемое возмущение.

Рассмотрим задачу синтеза системы регулирования на примере объекта с одним регулирующим воздействием и несколькими выходными переменными.

Множественный объект с одним регулирующим воздействием. Линейная модель множественного объекта управления в этом случае может быть представлена в виде:

,                                   

где  - матричная передаточная функция размером (); - количество каналов регулирования; - регулирующее воздействие;  - выходная переменная -го канала регулирования; - вектор коэффициентов размером ().

Критерий, учитывающий точность регулирования и заданное соотношение регулирующих воздействий может быть задан в виде:

,                            

где  - текущий момент времени;  - интервал времени оценки показателя качества.

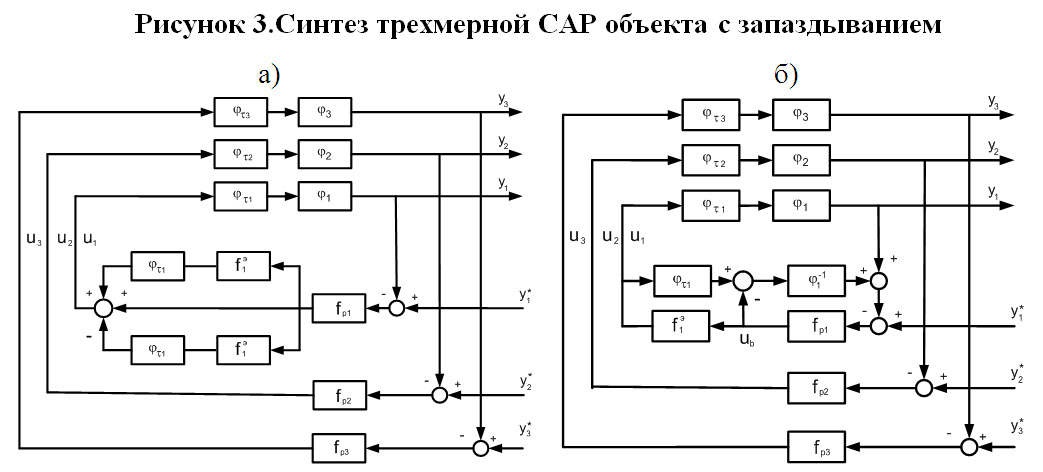
На рисунках 3 - 5 представлена процедура синтеза САР на примере множественного объекта с тремя управляемыми выходами с использованием эквивалентных структурных преобразований.

Решение задачи синтеза общей структуры САР для объекта с тремя управляющими воздействиями условно можно разделить на две части:

1.  Синтез трехмерной САР для объекта с с запаздыванием на основе системы - прототипа (рисунки 3а – 3б).

2.  Синтез блока распределения регулирующих воздействий.

В качестве системы - прототипа можно выбрать оптимальную трехмерную автономную САР для объекта без запаздывания.

Первый шаг – введение скомпенсированных цепочек с элементами, дополняющими каналы регулирования без запаздывания (рисунок 3) до объекта с запаздыванием в каналах регулирования.

На рисунке 3а иллюстрируется введение скомпенсированной цепочки  в первый канал регулирования.

После преобразований получим схему (рисунок 3б) для объекта с запаздыванием в первом канале регулирования.

Приведенное управление, в соответствии с рисунком 3б, определяется выражением:

                                           (1)

Разделим (1) на . Получим

В полосе частот, где  можно записать:

В соответствии с полученным выражением система регулирования может быть представлена в эквивалентном виде (рисунок 4а).

Аналогично, введя цепочки  и , выполнив необходимые преобразования, получим структуру трехмерной автономной системы регулирования для объекта с различными запаздываниями в каналах регулирования (рисунок 4б).

На втором шаге определяются значения  из условия (рисунок 5а):

 ,

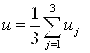 .                                                                                                                (2)

Структура полученной САР представлена на рисунке 5б. Формула 2 справедлива при равном распределении ресурса регулирования по всем каналам.

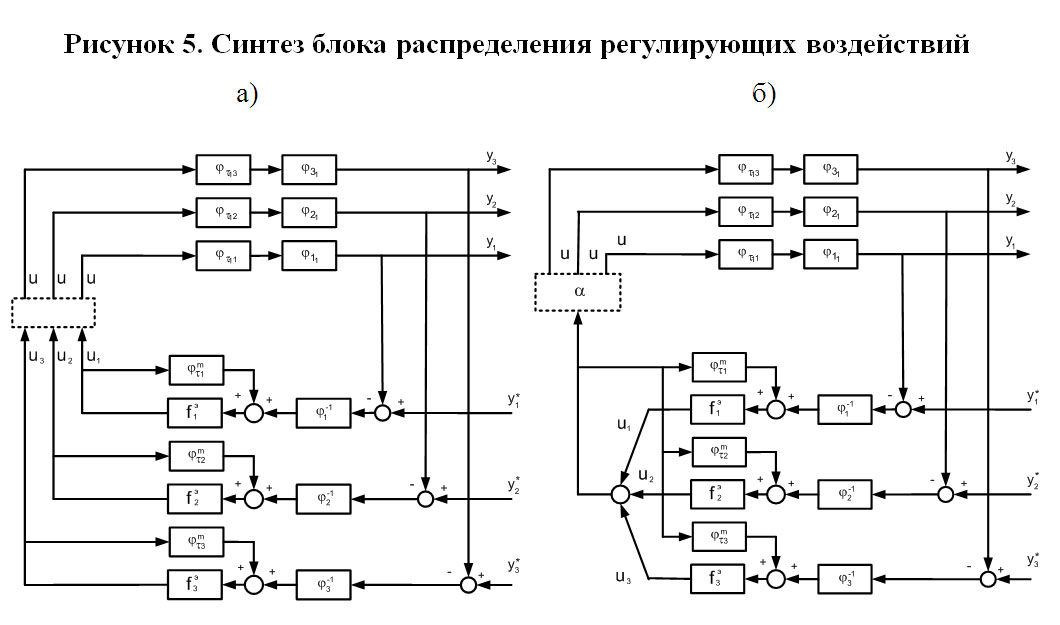
В общем случае выражение для расчета регулирующего воздействия можно записать как

.

Аналогичным образом синтезируется система регулирования для множественного объекта второго типа – с одной выходной переменной и несколькими управляющими воздействиями.  

Рассмотрим пример синтеза системы управления для  множественного объекта с двумя выходными переменными.

Модель объекта управления может быть представлена в виде:

,

где - изображение выходной переменой, управляющего и неконтролируемым возмущающим воздействием.

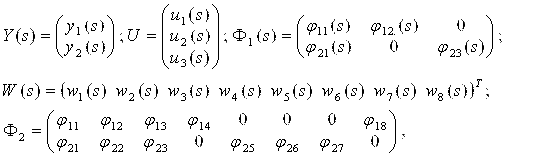
где  - передаточные функции по каналам преобразования управляющих и возмущающих воздействий.

Критерий качества можно записать в виде:

                               (3)

Рассматриваемый случай включает в себя, кроме этапов, перечисленных выше, синтез контуров компенсации контролируемых возмущений, а также компенсатора взаимосвязей контуров регулирования.

В качестве системы - прототипа принимается автономная двухмерная САР без запаздывания (рисунок 6а).

На рисунке 6б показано введение в систему – прототип скомпенсированной цепочки для синтеза третьего канала регулирования , где  оператор, задающий преобразование второго управляющего воздействия, - элемент, учитывающий различие физической природы каналов регулирования.

Синтез контуров компенсации контролируемых возмущений представлен на рисунке 6в. Показано введение двух скомпенсированных цепочек, отражающих факт влияния контролируемого возмущения W на степень металлизации и содержание углерода  и .

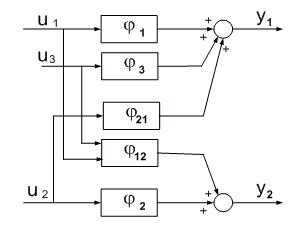
Построение компенсатора взаимосвязей контуров регулирования иллюстрируется на рисунке 6а, где представлено введение в объект регулирования элементов, образующих такую взаимосвязь .

На рисунке 6б приведена структура САР многомерного многосвязанного объекта с двумя управляемыми переменными, содержащая два автономных контура регулирования без запаздывания с одним контролируемым возмущением.

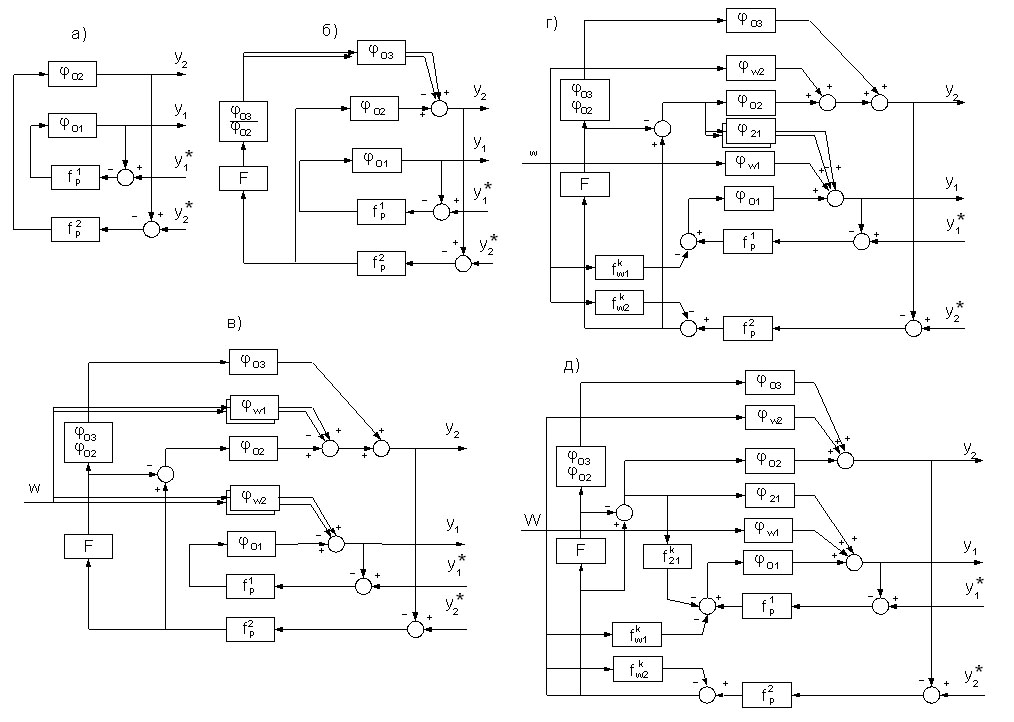
Рисунок 6. Этапы синтеза САР с двумя управляемыми входами

Дополнение объекта управления элементами запаздывания выполняется аналогично тому, как это было рассмотрено выше при синтезе САР группового дозатора, введением скомпенсированных цепочек как в каналы регулирования, так и в каналы преобразования контролируемых возмущений.

Конечная структура системы регулирования степени металлизации и содержания углерода приведена на рисунке 7.

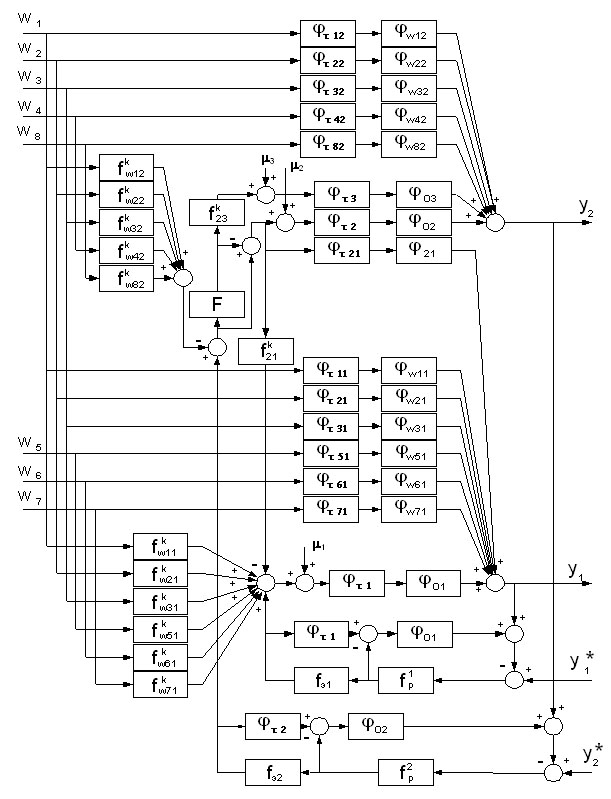
Рисунок 7. Структура САР объекта с двумя управляемыми выходами

Регулятор включает в себя два автономных контура регулирования по косвенно оцениваемым неконтролируемым возмущениям, каждый из которых включает  контур компенсации контролируемых возмущений. Автономность работы контуров регулирования обеспечивается компенсатором взаимосвязей .

Свойства синтезированной системы управления аналогичны рассмотренным выше для САР группового дозатора: во-первых, качество переходных процессов в автономных контурах регулирования (без контролируемых возмущений), при отсутствии ограничений на величину регулирующего воздействия в канале регулирования с минимальным запаздыванием не зависит от ошибок прогнозирования и реализации регулирующих воздействий по каналам регулирования с большим запаздыванием; во-вторых, длительность переходных процессов в контурах регулирования минимально возможная и определяется динамическими характеристиками канала регулирования с наименьшим запаздыванием. Действительно, легко показать, что в САР (см.рисунок 7) при   :

                   ,

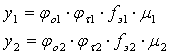и не зависит от .

Полученные структуры систем регулирования являются квазиоптимальными по критерию синтеза системы – прототипа [1, с. 34].   

Список литературы:

1.            Алгоритмизация управления процессами шихтоподготовки: Учебное пособие / Мышляев Л. П., Авдеев В. П., Киселев С. Ф., Марченко Ю. Н. -Новокузнецк, Кузбасский политехнический институт, 1989.-82 с.

2.            Прикладной анализ случайных данных. / Дж. Бендат, А. Пирсол. М., Мир,1989. 541 с.